新高考湖北专用 第五章 统计[必修3]5.3.1-5.3.2:26张PPT
文档属性
| 名称 | 新高考湖北专用 第五章 统计[必修3]5.3.1-5.3.2:26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 21:41:10 | ||
图片预览








文档简介
课件26张PPT。第五章 统计[必修3]5.3 变量间的相关关系
5.3.1 变量之间的相关关系
5.3.2 两个变量的线性相关1.相关关系的概念:变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有 的,那么这两个变量之间的关系叫作相关关系.?
2.两个变量间的关系:两个变量之间的关系分为 和 .?
3.散点图:将样本中n个数据点(xi,yi)(i=1,2,…,n)描在平面直角坐标系中,以表示具有相关关系的两个变量的一组数据的 叫作散点图.?预习探究随机性两个变量的线性相关知识点一函数关系相关关系图形4.正相关与负相关
(1)正相关:散点图中的点散布在从左下角到右上角的区域,这种相关称为 .?
(2)负相关:散点图中的点散布在从左上角到右下角的区域,这种相关称为 .?预习探究正相关负相关预习探究 [讨论] 相关关系与函数关系的区别和联系是什么?解:相同点:两者均是指两个变量间的关系.
不同点:(1)函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系;相关关系是一种非确定的关系,如一块农田的水稻产量与施肥量之间的关系.
(2)函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.例如,有人发现,对于在校儿童,鞋的大小与阅读能力有很强的相关关系,然而学会新词并不能使脚变大,而是涉及第三个因素——年龄,当儿童长大一些,他们的阅读能力会提高,而且由于长大脚也变大.预习探究回归直线的方程知识点二1.回归直线:如果散点图中点的分布从整体上看大致在 附近,就称这两个变量之间具有 关系,这条直线叫作回归直线.回归直线过 的中心.?
2.回归方程与最小二乘法
假设我们已经得到两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn),用Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2表示点到直线y=bx+a的“整体距离”,当Q最小时,a,b的值可由下列公式给出:一条直线线性相关样本点预习探究?考点类析例1 (1)下列变量之间的关系是函数关系的是( )
A.已知二次函数y=ax2+bx+c,其中a,c是已知常数,取b为自变量,自变量和这个函数的判别式Δ=b2-4ac
B.光照时间和果树亩产量
C.降雪量和交通事故发生率
D.每亩施用肥料量和粮食亩产量
变量之间的相关关系与散点图A[解析] (1)Δ=b2-4ac是一种确定的关系,即为函数关系.考点一考点类析例1 (2)如图5-3-1所示的是具有相关关系的两个变量的一组数据的散点图和回归直线,若去掉一个点后,剩下的5个点的线性相关关系最强,则应去掉( )
A.D点 B.E点 C.F点 D.A点
C[解析] (2)由散点图易知F点距回归直线最远,所以去掉F点后剩下的点线性相关关系最强.
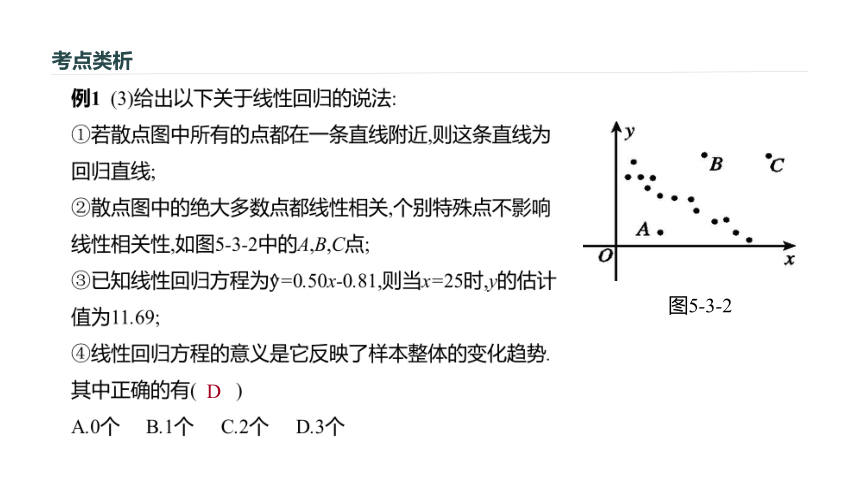
图5-3-1考点类析?D图5-3-2考点类析?考点类析回归直线方程的求法与应用考点二例2 某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
(1)画出散点图.
(2)y与x是否具有线性相关关系?若是,求y关于x的回归方程.解:(1)散点图如图所示.考点类析?考点类析变式 为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子的发芽数,得到如下资料:
该所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.考点类析?考点类析??考点类析?考点类析拓展 为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数:
?考点类析?考点类析?考点类析?考点类析?当堂自测[解析] “瑞雪兆丰年”和“读书破万卷,下笔如有神”是根据多年经验总结归纳出来的,“吸烟有害健康”具有科学根据,所以它们都是相关关系,所以A,B,C三个选项具有相关关系;结合生活经验知,喜鹊和乌鸦发出叫声是它们自身的生理反应,与喜和丧无任何关系,故选项D不具有相关关系.1.下列语句所表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年
B.读书破万卷,下笔如有神
C.吸烟有害健康
D.喜鹊叫喜,乌鸦叫丧D当堂自测[解析] x的系数为负数,表示负相关,排除B,D,由实际意义可知x>0,y>0,C中,易知散点图不经过第一象限,故选A.?A当堂自测??D当堂自测??B??当堂自测?5.某产品的广告费用x(单位:万元)与销售额y(单位:万元)的统计数据如下表:65.5万元
5.3.1 变量之间的相关关系
5.3.2 两个变量的线性相关1.相关关系的概念:变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有 的,那么这两个变量之间的关系叫作相关关系.?
2.两个变量间的关系:两个变量之间的关系分为 和 .?
3.散点图:将样本中n个数据点(xi,yi)(i=1,2,…,n)描在平面直角坐标系中,以表示具有相关关系的两个变量的一组数据的 叫作散点图.?预习探究随机性两个变量的线性相关知识点一函数关系相关关系图形4.正相关与负相关
(1)正相关:散点图中的点散布在从左下角到右上角的区域,这种相关称为 .?
(2)负相关:散点图中的点散布在从左上角到右下角的区域,这种相关称为 .?预习探究正相关负相关预习探究 [讨论] 相关关系与函数关系的区别和联系是什么?解:相同点:两者均是指两个变量间的关系.
不同点:(1)函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系;相关关系是一种非确定的关系,如一块农田的水稻产量与施肥量之间的关系.
(2)函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.例如,有人发现,对于在校儿童,鞋的大小与阅读能力有很强的相关关系,然而学会新词并不能使脚变大,而是涉及第三个因素——年龄,当儿童长大一些,他们的阅读能力会提高,而且由于长大脚也变大.预习探究回归直线的方程知识点二1.回归直线:如果散点图中点的分布从整体上看大致在 附近,就称这两个变量之间具有 关系,这条直线叫作回归直线.回归直线过 的中心.?
2.回归方程与最小二乘法
假设我们已经得到两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn),用Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2表示点到直线y=bx+a的“整体距离”,当Q最小时,a,b的值可由下列公式给出:一条直线线性相关样本点预习探究?考点类析例1 (1)下列变量之间的关系是函数关系的是( )
A.已知二次函数y=ax2+bx+c,其中a,c是已知常数,取b为自变量,自变量和这个函数的判别式Δ=b2-4ac
B.光照时间和果树亩产量
C.降雪量和交通事故发生率
D.每亩施用肥料量和粮食亩产量
变量之间的相关关系与散点图A[解析] (1)Δ=b2-4ac是一种确定的关系,即为函数关系.考点一考点类析例1 (2)如图5-3-1所示的是具有相关关系的两个变量的一组数据的散点图和回归直线,若去掉一个点后,剩下的5个点的线性相关关系最强,则应去掉( )
A.D点 B.E点 C.F点 D.A点
C[解析] (2)由散点图易知F点距回归直线最远,所以去掉F点后剩下的点线性相关关系最强.
图5-3-1考点类析?D图5-3-2考点类析?考点类析回归直线方程的求法与应用考点二例2 某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
(1)画出散点图.
(2)y与x是否具有线性相关关系?若是,求y关于x的回归方程.解:(1)散点图如图所示.考点类析?考点类析变式 为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子的发芽数,得到如下资料:
该所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.考点类析?考点类析??考点类析?考点类析拓展 为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数:
?考点类析?考点类析?考点类析?考点类析?当堂自测[解析] “瑞雪兆丰年”和“读书破万卷,下笔如有神”是根据多年经验总结归纳出来的,“吸烟有害健康”具有科学根据,所以它们都是相关关系,所以A,B,C三个选项具有相关关系;结合生活经验知,喜鹊和乌鸦发出叫声是它们自身的生理反应,与喜和丧无任何关系,故选项D不具有相关关系.1.下列语句所表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年
B.读书破万卷,下笔如有神
C.吸烟有害健康
D.喜鹊叫喜,乌鸦叫丧D当堂自测[解析] x的系数为负数,表示负相关,排除B,D,由实际意义可知x>0,y>0,C中,易知散点图不经过第一象限,故选A.?A当堂自测??D当堂自测??B??当堂自测?5.某产品的广告费用x(单位:万元)与销售额y(单位:万元)的统计数据如下表:65.5万元
同课章节目录
