新高考湖北专用 第五章 统计[必修3]本章总结提升:40张PPT
文档属性
| 名称 | 新高考湖北专用 第五章 统计[必修3]本章总结提升:40张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 21:46:15 | ||
图片预览









文档简介
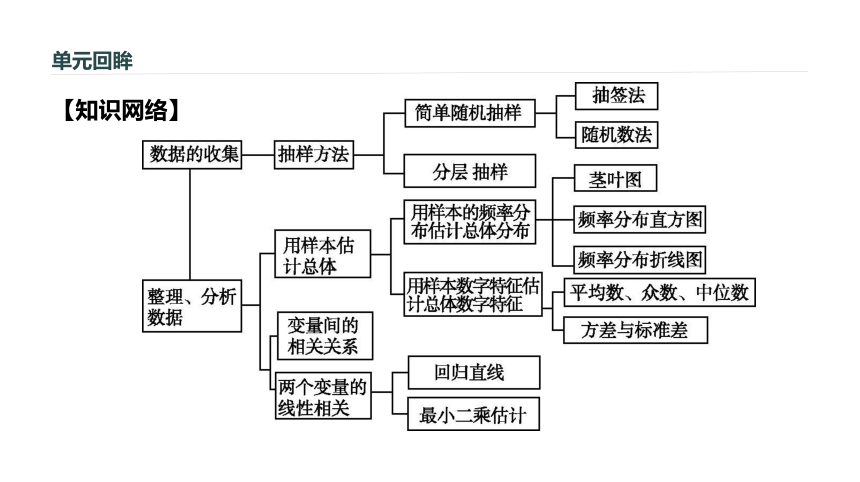
课件40张PPT。第五章 统计[必修3]本章总结提升 单元回眸【知识网络】判断下列说法是否正确.(请在括号中填写“√”或“×”)
1.抽签法和随机数法都是不放回抽样.( )
2.利用随机数表抽样时,开始位置和读数方向可以任意选择.( )
3.分层抽样中,为确保公平性,在每层都应用同一抽样方法.( )
4.频率分布直方图中每个小长方形的面积等于相应组的频率,各个小长方形面积之和小于1. ( )
5.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势.( )单元回眸【知识辨析】√××√√6.一组数据的方差越大,说明这组数据的波动越大.( )
7.从频率分布直方图中得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了.( )
8.从总体中抽取一个样本,用样本的分布估计总体的分布,样本容量越小估计越准确.( )
9.在样本数据中,频率分布最大值所对应的样本数据是众数.( )
10.一般茎叶图左侧的叶按从大到小的顺序写,右侧的叶按从小到大的顺序写,相同的数据可以只记一次.( )单元回眸√×√×√整合创新抽样方法的选取与应用题型一 [类型总述] (1)用简单随机抽样抽取样本;(2)用分层抽样抽取样本.
整合创新例1 (1)某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将50个同学按01,02,03,…,50进行编号,然后从随机数表第9行第11列开始向右读,则选出的第7个个体是( )
(注:表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.02 B.13 C.42 D.44
A[解析] (1)依题意,选取的数据依次为07,42,44,38,15,13,02,故第7个个体为02.
整合创新例1 (2)某中学有高中生3500人,初中生1500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150
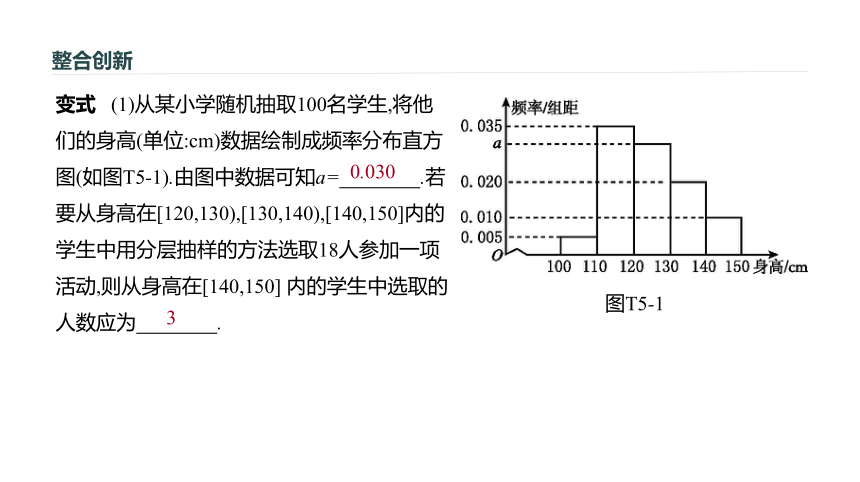
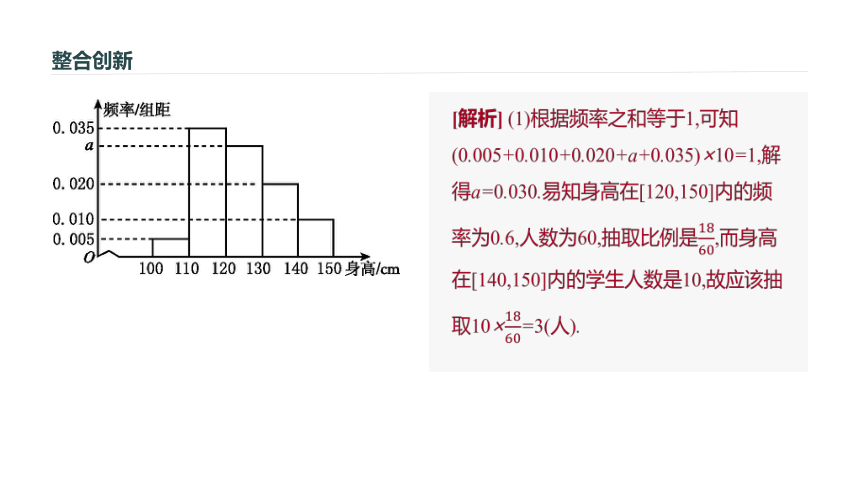
C.200 D.250A?整合创新例1 (3)某公司有大量客户,且不同年龄段客户对其服务的评价有较大差异,为了解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有抽签法、分层抽样和随机数表法,则最合适的抽样方法是 .分层抽样[解析] (3)由于个体差异明显,客户量大,根据分层抽样特点,最适合的抽样方法是分层抽样.整合创新变式 (1)从某小学随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图T5-1).由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]内的学生中用分层抽样的方法选取18人参加一项活动,则从身高在[140,150] 内的学生中选取的人数应为 .?
0.0303图T5-1整合创新?整合创新变式 (2)某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取 件.?
18?整合创新用样本的频率分布估计总体分布题型二例2 (1)在一次200千米的汽车拉力赛中,50名参赛选手的成绩全部介于13分钟到18分钟之间,将比赛成绩分为五组:第一组[13,14),第二组[14,15),…,第五组[17,18],其频率分布直方图如图T5-2所示,若成绩在[13,15)内的选手可获奖,则这50名选手中获奖的人数为( )
A.39 B.35 C.15 D.11
[类型总述] (1)茎叶图;(2)频率分布直方图.D图T5-2整合创新[解析] 由频率分布直方图知,成绩在[13,15)内的频率为(1-0.38-0.32-0.08)×1=0.22,所以成绩在[13,15)内的人数为50×0.22=11.故选D.
整合创新例2 (2)从高三学生中抽取50名学生参加数学竞赛,成绩(单位:分)的分组及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
①列出样本的频率分布表;
②估计成绩在[60,90)内的学生比例;
③估计成绩在85分以下的学生比例.
整合创新解:①频率分布表如下:?整合创新例3 (3)为了了解某城市居民用水量的情况,我们获得了100位居民某年的月均用水量(单位:t),通过对数据的处理,我们获得了这100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏).
100位居民月均用水量的频率分布表整合创新①确定表中x与y的值.
②求频率分布直方图中左数第4个矩形的高度.
③在频率分布直方图中画出频率分布折线图.
④我们想得到总体密度曲线,请回答我们应该怎么做?图T5-3整合创新解:①根据频率分布表中频数与频率的对应关系,补全频率分布表:
所以,x=25,y=0.06.
整合创新②因为左数第4个矩形对应的频率为0.22,从表中可知组距为0.5,所以它的高度为0.22÷0.5=0.44.
④为了得到总体密度曲线,我们可以让样本的容量增加,所分的组增加,组距减小,相应的频率折线图会越来越接近于一条光滑的曲线,即为总体密度曲线.
③整合创新变式 从某企业生产的产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
整合创新?图T5-4整合创新解:(1)填写频率分布表如下:整合创新画出频率分布直方图如下:整合创新?整合创新用样本的数字特征估计总体的数字特征题型三例3 (1)为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 ( )
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
[解析] (1)根据标准差的概念,可知标准差是刻画一组数据波动与稳定程度的一个量,所以选B. [类型总述] (1)求样本的平均数、中位数;(2)求样本的方差、标准差.B整合创新例3 (2)[2018·江苏卷] 已知5位裁判给某运动员打出的分数的茎叶图如图T5-5所示,那么这5位裁判打出的分数的平均数为 .?
?90图T5-5整合创新变式 (1)[2018·全国卷Ⅰ] 某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
使用了节水龙头50天的日用水量频数分布表整合创新①作出使用了节水龙头50天的日用水量数据的频率分布直方图:
②估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率.
③估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表)图T5-6整合创新解:(1)①
整合创新?整合创新变式 (2)汽车行业是碳排放量比较大的行业之一,欧盟规定,从2012年开始,对CO2排放量超过130 g/km的MI型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类MI型品牌的新车各抽取了5辆进行CO2排放量检测,记录如下(单位:g/km):
?整合创新?整合创新回归方程的应用 题型四 [类型总述] (1)散点图;(2)回归系数;(3)回归直线方程.整合创新例4 理论预测某城市2020年到2024年人口总数与年份的关系如下表所示:
?整合创新?整合创新变式 [2018·全国卷Ⅱ] 图T5-7是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.
图T5-7整合创新?整合创新?整合创新?整合创新 (ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.
(以上给出了2种理由,答出其中任意一种或其他合理理由均可)
1.抽签法和随机数法都是不放回抽样.( )
2.利用随机数表抽样时,开始位置和读数方向可以任意选择.( )
3.分层抽样中,为确保公平性,在每层都应用同一抽样方法.( )
4.频率分布直方图中每个小长方形的面积等于相应组的频率,各个小长方形面积之和小于1. ( )
5.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势.( )单元回眸【知识辨析】√××√√6.一组数据的方差越大,说明这组数据的波动越大.( )
7.从频率分布直方图中得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了.( )
8.从总体中抽取一个样本,用样本的分布估计总体的分布,样本容量越小估计越准确.( )
9.在样本数据中,频率分布最大值所对应的样本数据是众数.( )
10.一般茎叶图左侧的叶按从大到小的顺序写,右侧的叶按从小到大的顺序写,相同的数据可以只记一次.( )单元回眸√×√×√整合创新抽样方法的选取与应用题型一 [类型总述] (1)用简单随机抽样抽取样本;(2)用分层抽样抽取样本.
整合创新例1 (1)某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将50个同学按01,02,03,…,50进行编号,然后从随机数表第9行第11列开始向右读,则选出的第7个个体是( )
(注:表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.02 B.13 C.42 D.44
A[解析] (1)依题意,选取的数据依次为07,42,44,38,15,13,02,故第7个个体为02.
整合创新例1 (2)某中学有高中生3500人,初中生1500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150
C.200 D.250A?整合创新例1 (3)某公司有大量客户,且不同年龄段客户对其服务的评价有较大差异,为了解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有抽签法、分层抽样和随机数表法,则最合适的抽样方法是 .分层抽样[解析] (3)由于个体差异明显,客户量大,根据分层抽样特点,最适合的抽样方法是分层抽样.整合创新变式 (1)从某小学随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图T5-1).由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]内的学生中用分层抽样的方法选取18人参加一项活动,则从身高在[140,150] 内的学生中选取的人数应为 .?
0.0303图T5-1整合创新?整合创新变式 (2)某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取 件.?
18?整合创新用样本的频率分布估计总体分布题型二例2 (1)在一次200千米的汽车拉力赛中,50名参赛选手的成绩全部介于13分钟到18分钟之间,将比赛成绩分为五组:第一组[13,14),第二组[14,15),…,第五组[17,18],其频率分布直方图如图T5-2所示,若成绩在[13,15)内的选手可获奖,则这50名选手中获奖的人数为( )
A.39 B.35 C.15 D.11
[类型总述] (1)茎叶图;(2)频率分布直方图.D图T5-2整合创新[解析] 由频率分布直方图知,成绩在[13,15)内的频率为(1-0.38-0.32-0.08)×1=0.22,所以成绩在[13,15)内的人数为50×0.22=11.故选D.
整合创新例2 (2)从高三学生中抽取50名学生参加数学竞赛,成绩(单位:分)的分组及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
①列出样本的频率分布表;
②估计成绩在[60,90)内的学生比例;
③估计成绩在85分以下的学生比例.
整合创新解:①频率分布表如下:?整合创新例3 (3)为了了解某城市居民用水量的情况,我们获得了100位居民某年的月均用水量(单位:t),通过对数据的处理,我们获得了这100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏).
100位居民月均用水量的频率分布表整合创新①确定表中x与y的值.
②求频率分布直方图中左数第4个矩形的高度.
③在频率分布直方图中画出频率分布折线图.
④我们想得到总体密度曲线,请回答我们应该怎么做?图T5-3整合创新解:①根据频率分布表中频数与频率的对应关系,补全频率分布表:
所以,x=25,y=0.06.
整合创新②因为左数第4个矩形对应的频率为0.22,从表中可知组距为0.5,所以它的高度为0.22÷0.5=0.44.
④为了得到总体密度曲线,我们可以让样本的容量增加,所分的组增加,组距减小,相应的频率折线图会越来越接近于一条光滑的曲线,即为总体密度曲线.
③整合创新变式 从某企业生产的产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
整合创新?图T5-4整合创新解:(1)填写频率分布表如下:整合创新画出频率分布直方图如下:整合创新?整合创新用样本的数字特征估计总体的数字特征题型三例3 (1)为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 ( )
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
[解析] (1)根据标准差的概念,可知标准差是刻画一组数据波动与稳定程度的一个量,所以选B. [类型总述] (1)求样本的平均数、中位数;(2)求样本的方差、标准差.B整合创新例3 (2)[2018·江苏卷] 已知5位裁判给某运动员打出的分数的茎叶图如图T5-5所示,那么这5位裁判打出的分数的平均数为 .?
?90图T5-5整合创新变式 (1)[2018·全国卷Ⅰ] 某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
使用了节水龙头50天的日用水量频数分布表整合创新①作出使用了节水龙头50天的日用水量数据的频率分布直方图:
②估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率.
③估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表)图T5-6整合创新解:(1)①
整合创新?整合创新变式 (2)汽车行业是碳排放量比较大的行业之一,欧盟规定,从2012年开始,对CO2排放量超过130 g/km的MI型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类MI型品牌的新车各抽取了5辆进行CO2排放量检测,记录如下(单位:g/km):
?整合创新?整合创新回归方程的应用 题型四 [类型总述] (1)散点图;(2)回归系数;(3)回归直线方程.整合创新例4 理论预测某城市2020年到2024年人口总数与年份的关系如下表所示:
?整合创新?整合创新变式 [2018·全国卷Ⅱ] 图T5-7是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.
图T5-7整合创新?整合创新?整合创新?整合创新 (ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.
(以上给出了2种理由,答出其中任意一种或其他合理理由均可)
同课章节目录
