人教版九年级数学上册第二十二章二次函数22.1.4y=ax2+bx+c的图像和性质练习题含答案
文档属性
| 名称 | 人教版九年级数学上册第二十二章二次函数22.1.4y=ax2+bx+c的图像和性质练习题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 118.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-17 00:00:00 | ||
图片预览


文档简介
二次函数y=ax2+bx+c(a≠0)的图象与性质
知识点回顾
一、二次函数与之间的相互关系
1.顶点式化成一般式
从函数解析式我们可以直接得到抛物线的顶点(h,k),所以我们称为顶点式,将顶点式去括号,合并同类项就可化成一般式.
2.一般式化成顶点式
.
对照,可知,.
∴ 抛物线的对称轴是直线,顶点坐标是.
要点诠释:
1.抛物线的对称轴是直线,顶点坐标是,可以当作公式加以记忆和运用.
2.求抛物线的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.
二、二次函数的图象的画法
1.一般方法:列表、描点、连线;
2.简易画法:五点定形法.
其步骤为:
(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M,并用虚线画出对称轴.
(2)求抛物线与坐标轴的交点,
当抛物线与x轴有两个交点时,描出这两个交点A、B及抛物线与y轴的交点C,再找到点C关于对称轴的对称点D,将A、B、C、D及M这五个点按从左到右的顺序用平滑曲线连结起来.
要点诠释:
当抛物线与x轴只有一个交点或无交点时,描出抛物线与y轴的交点C及对称点D,由C、M、D三点可粗略地画出二次函数图象的草图;如果需要画出比较精确的图象,可再描出一对对称点A、B,然后顺次用平滑曲线连结五点,画出二次函数的图象,
三、二次函数的图象与性质
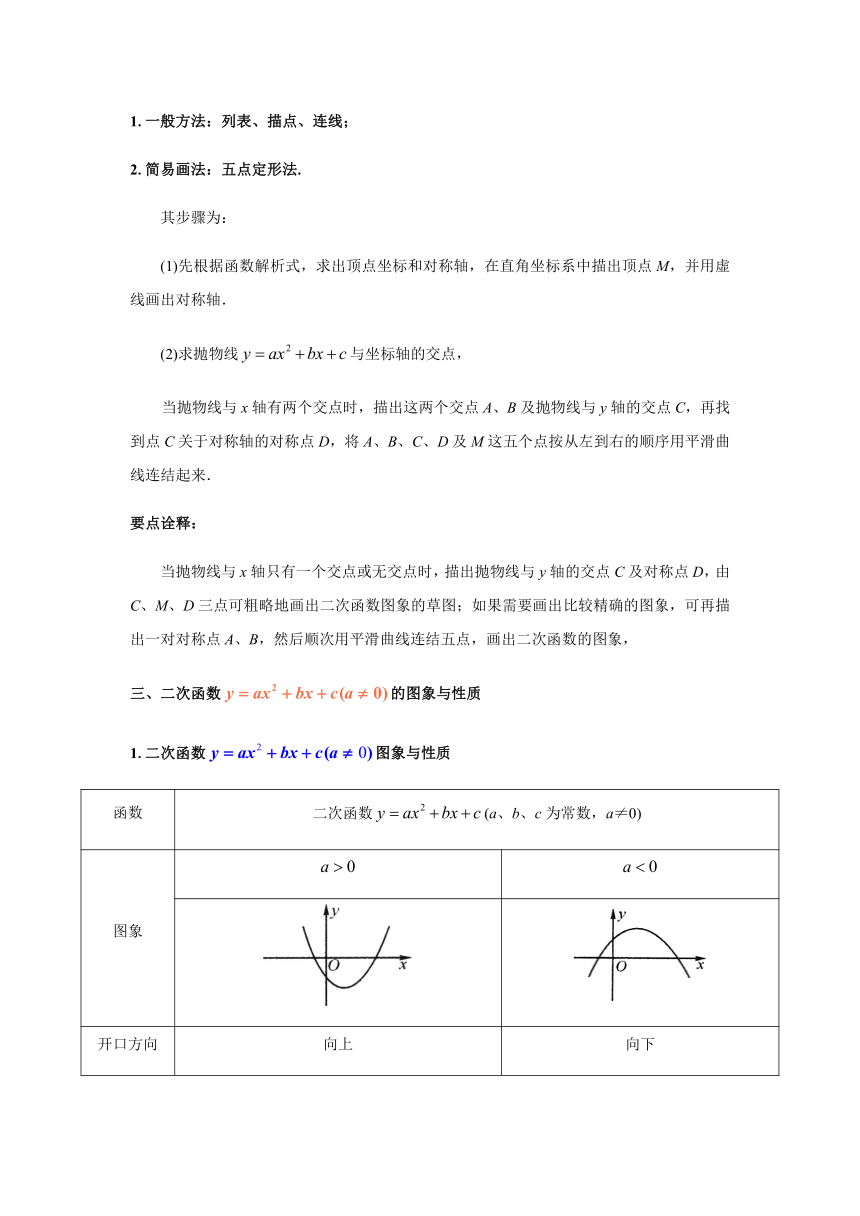
1.二次函数图象与性质
函数 二次函数(a、b、c为常数,a≠0)
图象
开口方向 向上 向下
对称轴 直线 直线
顶点坐标
增减性 在对称轴的左侧,即当时,y随x的增大而减小;在对称轴的右侧,即当时,y随x的增大而增大.简记:左减右增 在对称轴的左侧,即当时,y随x的增大而增大;在对称轴的右侧,即当时,y随x的增大而减小.简记:左增右减
最大(小)值 抛物线有最低点,当时,y有最小值, 抛物线有最高点,当时,y有最大值,
课后作业
◆基础
1. 函数的图象顶点坐标是( )
A. B. C. D.
2. 已知二次函数的图象如图1所示,则下列关于,,间的关系判断正确的是( )
A.<0 B. <0 C. D.
图1 图2 图3
3.二次函数,当x= 时,y有最 值为 .
4. 如图2所示的抛物线是二次函数的图象,那么的值是 .
5. 已知二次函数(是常数),与的部分对应值如下表,则当满足的条件是 时,;当满足的条件是 时,.
0 1 2 3
0 2 0
◆能力拓展
6. 如图3,二次函数图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求C的坐标;(2)求二次函数的解析式,并求出函数最大值。
7.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
X(元) 15 20 30 …
y(件) 25 20 10 …
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)是销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元? 此时每日的销售利润是多少元?
◆创新
8.如图,对称轴为直线x=的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
参考答案
1.C 2.D 3. 大 4 4.-1
5.0或2 0<<2
6.(1)C(0,5)
(2)
7.(1)设此一次函数关系式为,
则{,解得
故一次函数的关系式为.
(2)设所获利润为元,
则
所以产品的销售价应定为25元,此时每日的销售利润为225元.
8.(1)由抛物线的对称轴是,可设解析式为.
把A、B两点坐标代入上式,得
解之,得
故抛物线解析式为,顶点为
(2)∵点在抛物线上,位于第四象限,且坐标适合.
,
∴y<0,即 -y>0,-y表示点E到OA的距离.
∵OA是的对角线,
∴.
因为抛物线与轴的两个交点是(1,0)的(6,0),
所以,自变量的取值范围是1<<6.
①根据题意,当S = 24时,即.
化简,得 解之,得
故所求的点E有两个,分别为E1(3,-4),E2(4,-4).
点E1(3,-4)满足OE = AE,所以是菱形;
点E2(4,-4)不满足OE = AE,所以不是菱形.
②当OA⊥EF,且OA = EF时,是正方形,
此时点E的坐标只能是(3,-3).
而坐标为(3,-3)的点不在抛物线上,
故不存在这样的点E,使为正方形.
知识点回顾
一、二次函数与之间的相互关系
1.顶点式化成一般式
从函数解析式我们可以直接得到抛物线的顶点(h,k),所以我们称为顶点式,将顶点式去括号,合并同类项就可化成一般式.
2.一般式化成顶点式
.
对照,可知,.
∴ 抛物线的对称轴是直线,顶点坐标是.
要点诠释:
1.抛物线的对称轴是直线,顶点坐标是,可以当作公式加以记忆和运用.
2.求抛物线的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.
二、二次函数的图象的画法
1.一般方法:列表、描点、连线;
2.简易画法:五点定形法.
其步骤为:
(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M,并用虚线画出对称轴.
(2)求抛物线与坐标轴的交点,
当抛物线与x轴有两个交点时,描出这两个交点A、B及抛物线与y轴的交点C,再找到点C关于对称轴的对称点D,将A、B、C、D及M这五个点按从左到右的顺序用平滑曲线连结起来.
要点诠释:
当抛物线与x轴只有一个交点或无交点时,描出抛物线与y轴的交点C及对称点D,由C、M、D三点可粗略地画出二次函数图象的草图;如果需要画出比较精确的图象,可再描出一对对称点A、B,然后顺次用平滑曲线连结五点,画出二次函数的图象,
三、二次函数的图象与性质
1.二次函数图象与性质
函数 二次函数(a、b、c为常数,a≠0)
图象
开口方向 向上 向下
对称轴 直线 直线
顶点坐标
增减性 在对称轴的左侧,即当时,y随x的增大而减小;在对称轴的右侧,即当时,y随x的增大而增大.简记:左减右增 在对称轴的左侧,即当时,y随x的增大而增大;在对称轴的右侧,即当时,y随x的增大而减小.简记:左增右减
最大(小)值 抛物线有最低点,当时,y有最小值, 抛物线有最高点,当时,y有最大值,
课后作业
◆基础
1. 函数的图象顶点坐标是( )
A. B. C. D.
2. 已知二次函数的图象如图1所示,则下列关于,,间的关系判断正确的是( )
A.<0 B. <0 C. D.
图1 图2 图3
3.二次函数,当x= 时,y有最 值为 .
4. 如图2所示的抛物线是二次函数的图象,那么的值是 .
5. 已知二次函数(是常数),与的部分对应值如下表,则当满足的条件是 时,;当满足的条件是 时,.
0 1 2 3
0 2 0
◆能力拓展
6. 如图3,二次函数图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求C的坐标;(2)求二次函数的解析式,并求出函数最大值。
7.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
X(元) 15 20 30 …
y(件) 25 20 10 …
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)是销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元? 此时每日的销售利润是多少元?
◆创新
8.如图,对称轴为直线x=的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
参考答案
1.C 2.D 3. 大 4 4.-1
5.0或2 0<<2
6.(1)C(0,5)
(2)
7.(1)设此一次函数关系式为,
则{,解得
故一次函数的关系式为.
(2)设所获利润为元,
则
所以产品的销售价应定为25元,此时每日的销售利润为225元.
8.(1)由抛物线的对称轴是,可设解析式为.
把A、B两点坐标代入上式,得
解之,得
故抛物线解析式为,顶点为
(2)∵点在抛物线上,位于第四象限,且坐标适合.
,
∴y<0,即 -y>0,-y表示点E到OA的距离.
∵OA是的对角线,
∴.
因为抛物线与轴的两个交点是(1,0)的(6,0),
所以,自变量的取值范围是1<<6.
①根据题意,当S = 24时,即.
化简,得 解之,得
故所求的点E有两个,分别为E1(3,-4),E2(4,-4).
点E1(3,-4)满足OE = AE,所以是菱形;
点E2(4,-4)不满足OE = AE,所以不是菱形.
②当OA⊥EF,且OA = EF时,是正方形,
此时点E的坐标只能是(3,-3).
而坐标为(3,-3)的点不在抛物线上,
故不存在这样的点E,使为正方形.
同课章节目录
