2019湘教版数学八年级上册第二章三角形2.5 全等三角形课件(3课时共42张)
文档属性
| 名称 | 2019湘教版数学八年级上册第二章三角形2.5 全等三角形课件(3课时共42张) |

|
|
| 格式 | zip | ||
| 文件大小 | 612.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 00:00:00 | ||
图片预览



文档简介
课件42张PPT。教学课件
数学 八年级上册 湘教版
第2章 三角形
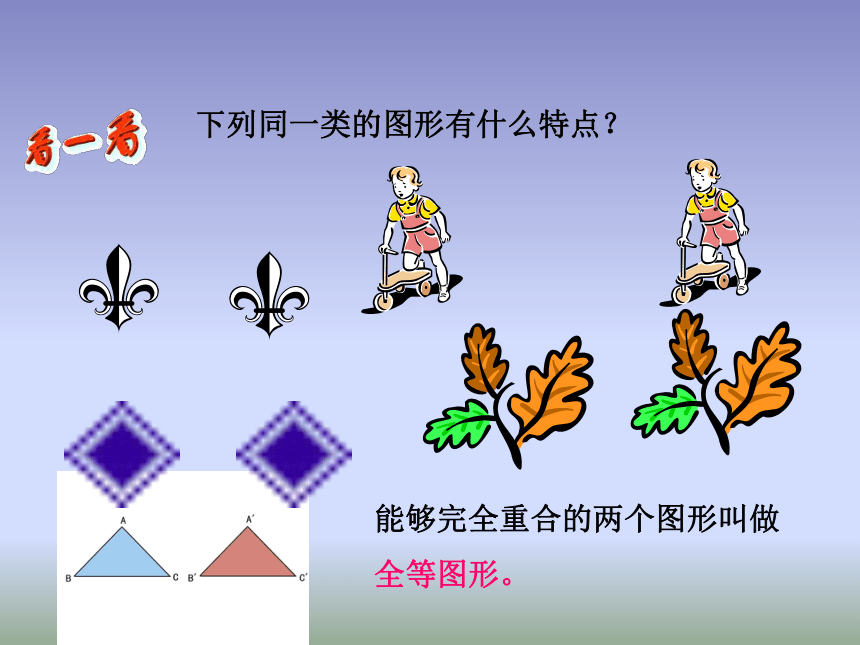
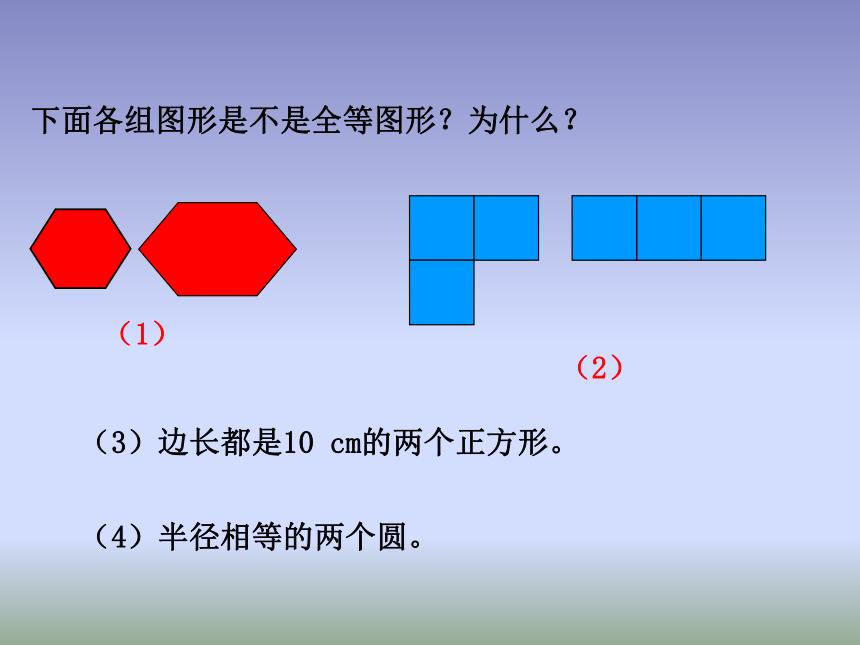
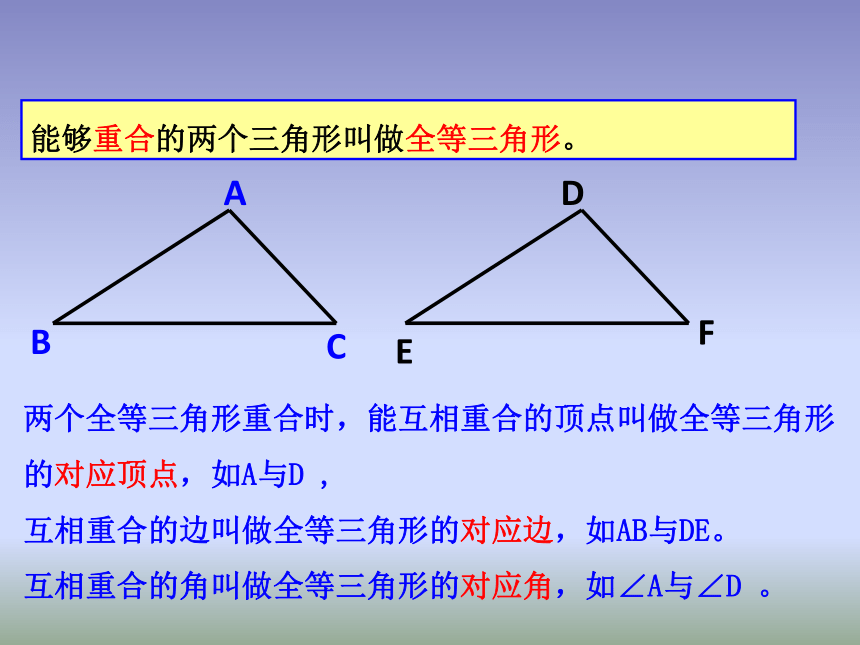
2.5 全等三角形能够完全重合的两个图形叫做全等图形。下列同一类的图形有什么特点?下面各组图形是不是全等图形?为什么?(1)(2)(3)边长都是10 cm的两个正方形。(4)半径相等的两个圆。两个全等三角形重合时,能互相重合的顶点叫做全等三角形的对应顶点,如A与D ,
互相重合的边叫做全等三角形的对应边,如AB与DE。
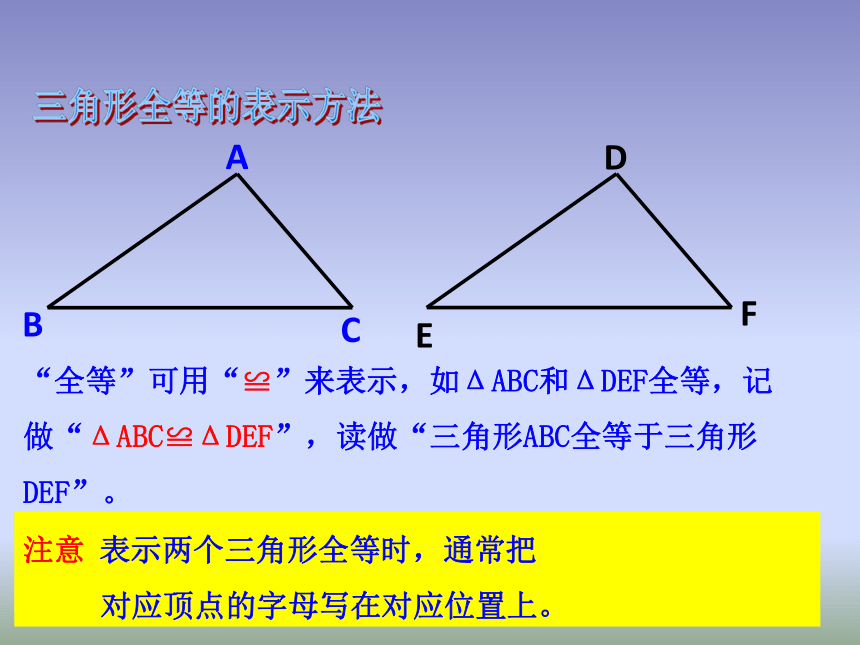
互相重合的角叫做全等三角形的对应角,如∠A与∠D 。能够重合的两个三角形叫做全等三角形。三角形全等的表示方法“全等”可用“≌”来表示,如ΔABC和ΔDEF全等,记做“ΔABC≌ΔDEF”,读做“三角形ABC全等于三角形DEF”。注意 表示两个三角形全等时,通常把
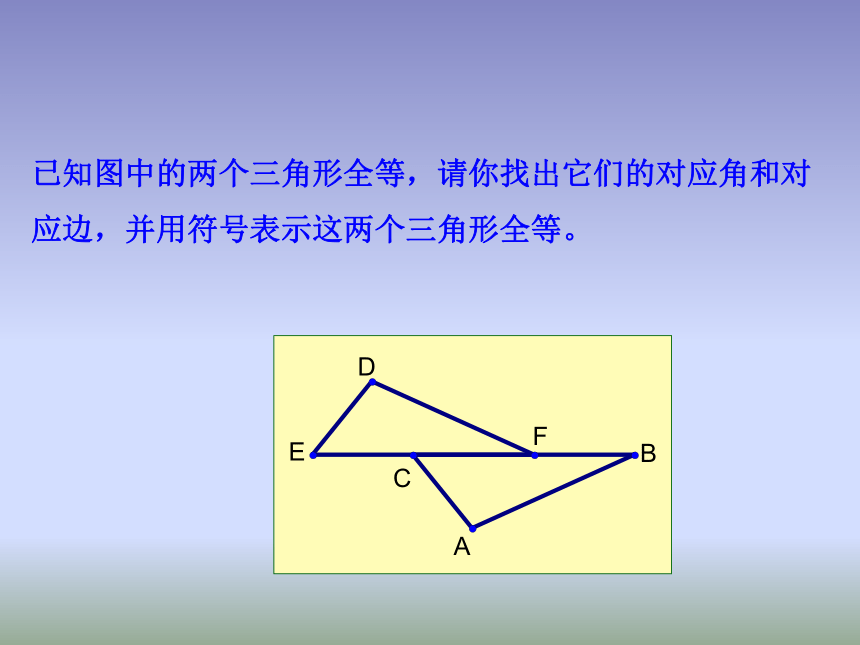
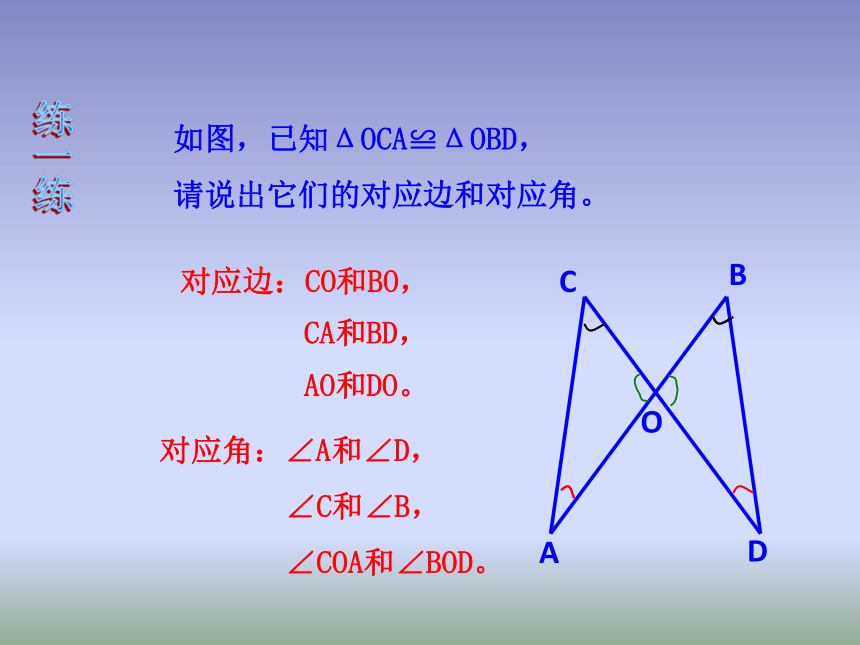
对应顶点的字母写在对应位置上。已知图中的两个三角形全等,请你找出它们的对应角和对应边,并用符号表示这两个三角形全等。练一练如图,已知ΔOCA≌ΔOBD,
请说出它们的对应边和对应角。ODCBA对应边:CO和BO,对应角:∠A和∠D,
∠C和∠B,
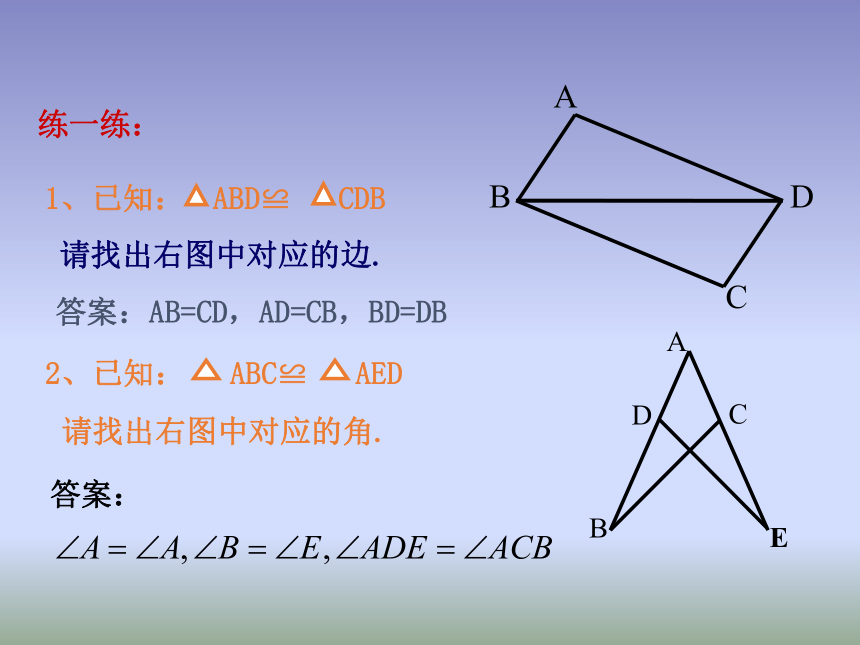
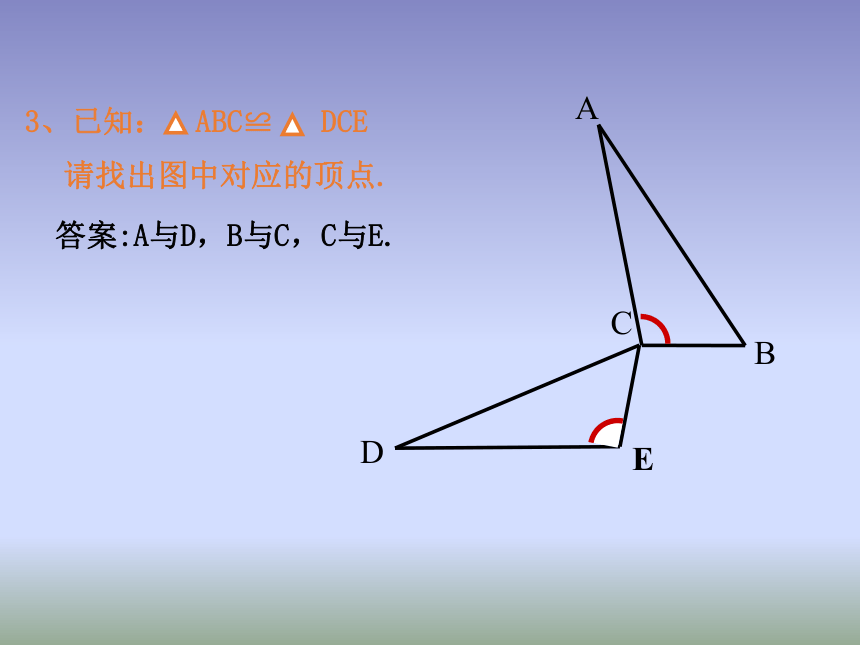
∠COA和∠BOD。AO和DO。CA和BD,答案:AB=CD,AD=CB,BD=DB练一练:请找出右图中对应的边.1、已知:2、已知:请找出右图中对应的角.答案:答案:A与D,B与C,C与E.总结寻找对应元素的规律(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
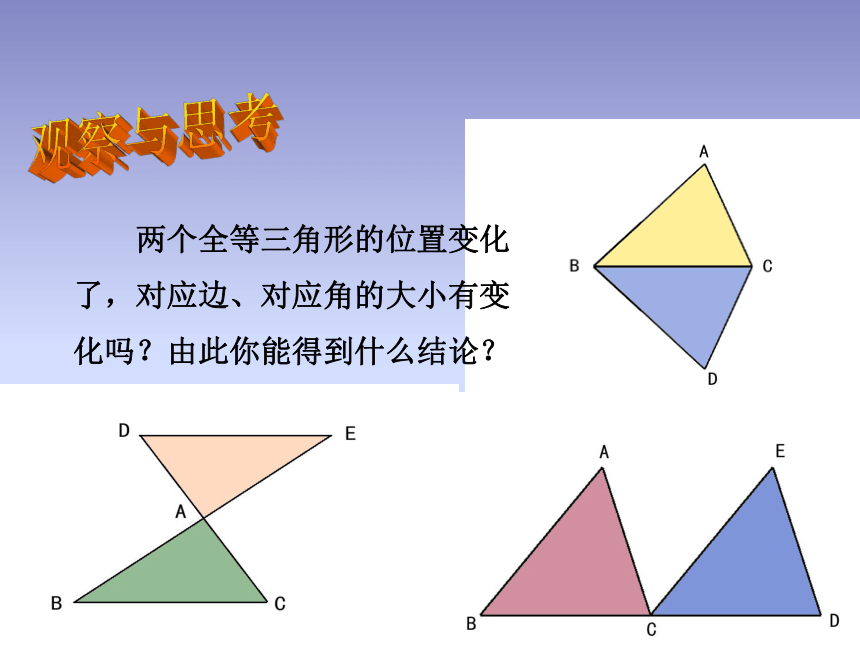
两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?观察与思考全等三角形的对应边相等,对应角相等。 ∵△ABC≌ △DFE ,
∴ AB=DF, BC=FE, AC=DE
( ),
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E ( ).全等三角形的性质应用全等三角形的对应边相等 全等三角形的对应角相等例题 如图,AD平分∠BAC,AB=AC. △ABD和△ACD全等吗?BD与CD相等吗? ∠B与∠C呢?请说明理由.1、能够 的两个图形叫全等形;
2、两个全等三角形重合时,互相重合的顶点叫做 ;互相重合的边叫做 ;互相重合的角叫做 ;
3、全等三角形的对应边 ,对应角 ;完全重合对应顶点对应边对应角相等相等小结4、记两个三角形全等时,通常把表示对应顶点的字母写在 ;例如△ABC≌ △DFE ,对应顶点分别是 .
5、两个三角形全等时,对应顶点所在的角是 ,对应边所对的角是 ,对应角所对的边是
。
对应位置点A和点D、点B和点F、点C和点E对应角对应角对应边 2.5 全等三角形(2)
三角形全等的判定定理(SAS)思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件的三个时,有四种情况:不能!???继续探讨三角形全等的条件:两边一角思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?图一图二在图一中, ∠A是AB和AC的夹角,
符合图一的条件,它可称为“两边及其夹角”。符合图二的条件,通常说成“两边和其中一边的对角” 在纸上的不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm.将这两个三角形叠在一起,它们完全重合吗?由此你能得到什么结论? (1)△ABC 和△A′B′C′ 的位置关系如图2-38.
图2-38A’B’C’在△ABC 和△A′B′C′中,∠ABC=∠A′B′C′ ,
AB=A′B′,BC =B′C′ .(2)△ABC和△A’B’C’ 的位置关系如图2-39.
图2-39在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,
AB=A’B’, BC=B’C’ .
(3)△ABC和△A’B’C’ 的位置关系如图2-40.
图2-40在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,
AB=A’B’, BC=B’C’ .
(4)△ABC和△A’B’C’ 的位置关系如图2-41.
图2-41CAB在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’,
AB=A’B’, BC=B’C’.
两边及其夹角分别相等的两个三角形全等.
(可简写成“边角边”或“SAS”).S ——边 A——角注意:两边和其中一边的对角分别相等的两个三角形 不一定全等.(即没有“边边角”或“SSA”这种判定定理).例2 已知:如图2-42,AB和CD相交于点O,且AO=BO,CO=DO.求证:△ACO ≌△BDO.“边角边”图2-42举
例 (3)全等三角形的判定 SSS1.掌握三角形全等的“边边边”定理.
2.了解三角形的稳定性.
3.经历探索三角形全等条件的过程,体会利用“边边边”定理操作、归纳、获得数学结论的过程. ①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F 1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。2、 全等三角形有什么性质?①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F1.满足这六个条件可以保证△ABC ≌△ DEF吗?
2.如果只满足这些条件中的一部分,那么能保证△ABC ≌
△DEF吗?思考:①三角;②三边;③两边一角;④两角一边。 3.如果满足三个条件,你能说出有哪几种可能的情况?探索三角形全等的条件已知两个三角形的三个内角分别为30°,60° ,90°,它们一定全等吗? 这说明有三个角对应相等的两个三角形
不一定全等⑴三个角已知两个三角形的三条边都分别为3cm、4cm、6cm 。它们一定全等吗?⑵三条边问题:把你画的三角形与其他同学所画的三
角形进行比较,它们能够互相重合吗?三角形全等的条件:
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)探索三角形全等的条件证明:∵BD=CE,
∴ BD-ED=CE-ED,即BE=CD。 例 如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ADC 当堂测试如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF.求证:①△ADE≌△CBF;②∠A=∠C.
∴△ADE≌△CBF,
∴∠A=∠C.全等三角形的判定AAS两边分别相等且其一组等边的对角相等的两个三角形不一定全等3cm2.5cm2.5cm3cm45°45°两角一夹边(ASA)两角一对边(AAS)? 引入新课1.掌握三角形全等的“角角边”定理.
2.能根据条件选择合适的判定方法进行推理论证.在△ABC与△DEF中,AB=DE, ∠A= ∠D, ∠C= ∠F.预习反馈角角边定理:两角分别相等及其中一组等角的对边也相等的两个三角形全等 (AAS) .预习反馈
数学 八年级上册 湘教版
第2章 三角形
2.5 全等三角形能够完全重合的两个图形叫做全等图形。下列同一类的图形有什么特点?下面各组图形是不是全等图形?为什么?(1)(2)(3)边长都是10 cm的两个正方形。(4)半径相等的两个圆。两个全等三角形重合时,能互相重合的顶点叫做全等三角形的对应顶点,如A与D ,
互相重合的边叫做全等三角形的对应边,如AB与DE。
互相重合的角叫做全等三角形的对应角,如∠A与∠D 。能够重合的两个三角形叫做全等三角形。三角形全等的表示方法“全等”可用“≌”来表示,如ΔABC和ΔDEF全等,记做“ΔABC≌ΔDEF”,读做“三角形ABC全等于三角形DEF”。注意 表示两个三角形全等时,通常把
对应顶点的字母写在对应位置上。已知图中的两个三角形全等,请你找出它们的对应角和对应边,并用符号表示这两个三角形全等。练一练如图,已知ΔOCA≌ΔOBD,
请说出它们的对应边和对应角。ODCBA对应边:CO和BO,对应角:∠A和∠D,
∠C和∠B,
∠COA和∠BOD。AO和DO。CA和BD,答案:AB=CD,AD=CB,BD=DB练一练:请找出右图中对应的边.1、已知:2、已知:请找出右图中对应的角.答案:答案:A与D,B与C,C与E.总结寻找对应元素的规律(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?观察与思考全等三角形的对应边相等,对应角相等。 ∵△ABC≌ △DFE ,
∴ AB=DF, BC=FE, AC=DE
( ),
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E ( ).全等三角形的性质应用全等三角形的对应边相等 全等三角形的对应角相等例题 如图,AD平分∠BAC,AB=AC. △ABD和△ACD全等吗?BD与CD相等吗? ∠B与∠C呢?请说明理由.1、能够 的两个图形叫全等形;
2、两个全等三角形重合时,互相重合的顶点叫做 ;互相重合的边叫做 ;互相重合的角叫做 ;
3、全等三角形的对应边 ,对应角 ;完全重合对应顶点对应边对应角相等相等小结4、记两个三角形全等时,通常把表示对应顶点的字母写在 ;例如△ABC≌ △DFE ,对应顶点分别是 .
5、两个三角形全等时,对应顶点所在的角是 ,对应边所对的角是 ,对应角所对的边是
。
对应位置点A和点D、点B和点F、点C和点E对应角对应角对应边 2.5 全等三角形(2)
三角形全等的判定定理(SAS)思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件的三个时,有四种情况:不能!???继续探讨三角形全等的条件:两边一角思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?图一图二在图一中, ∠A是AB和AC的夹角,
符合图一的条件,它可称为“两边及其夹角”。符合图二的条件,通常说成“两边和其中一边的对角” 在纸上的不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm.将这两个三角形叠在一起,它们完全重合吗?由此你能得到什么结论? (1)△ABC 和△A′B′C′ 的位置关系如图2-38.
图2-38A’B’C’在△ABC 和△A′B′C′中,∠ABC=∠A′B′C′ ,
AB=A′B′,BC =B′C′ .(2)△ABC和△A’B’C’ 的位置关系如图2-39.
图2-39在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,
AB=A’B’, BC=B’C’ .
(3)△ABC和△A’B’C’ 的位置关系如图2-40.
图2-40在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,
AB=A’B’, BC=B’C’ .
(4)△ABC和△A’B’C’ 的位置关系如图2-41.
图2-41CAB在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’,
AB=A’B’, BC=B’C’.
两边及其夹角分别相等的两个三角形全等.
(可简写成“边角边”或“SAS”).S ——边 A——角注意:两边和其中一边的对角分别相等的两个三角形 不一定全等.(即没有“边边角”或“SSA”这种判定定理).例2 已知:如图2-42,AB和CD相交于点O,且AO=BO,CO=DO.求证:△ACO ≌△BDO.“边角边”图2-42举
例 (3)全等三角形的判定 SSS1.掌握三角形全等的“边边边”定理.
2.了解三角形的稳定性.
3.经历探索三角形全等条件的过程,体会利用“边边边”定理操作、归纳、获得数学结论的过程. ①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F 1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。2、 全等三角形有什么性质?①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F1.满足这六个条件可以保证△ABC ≌△ DEF吗?
2.如果只满足这些条件中的一部分,那么能保证△ABC ≌
△DEF吗?思考:①三角;②三边;③两边一角;④两角一边。 3.如果满足三个条件,你能说出有哪几种可能的情况?探索三角形全等的条件已知两个三角形的三个内角分别为30°,60° ,90°,它们一定全等吗? 这说明有三个角对应相等的两个三角形
不一定全等⑴三个角已知两个三角形的三条边都分别为3cm、4cm、6cm 。它们一定全等吗?⑵三条边问题:把你画的三角形与其他同学所画的三
角形进行比较,它们能够互相重合吗?三角形全等的条件:
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)探索三角形全等的条件证明:∵BD=CE,
∴ BD-ED=CE-ED,即BE=CD。 例 如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ADC 当堂测试如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF.求证:①△ADE≌△CBF;②∠A=∠C.
∴△ADE≌△CBF,
∴∠A=∠C.全等三角形的判定AAS两边分别相等且其一组等边的对角相等的两个三角形不一定全等3cm2.5cm2.5cm3cm45°45°两角一夹边(ASA)两角一对边(AAS)? 引入新课1.掌握三角形全等的“角角边”定理.
2.能根据条件选择合适的判定方法进行推理论证.在△ABC与△DEF中,AB=DE, ∠A= ∠D, ∠C= ∠F.预习反馈角角边定理:两角分别相等及其中一组等角的对边也相等的两个三角形全等 (AAS) .预习反馈
同课章节目录
