湘教版八年级数学上册第一章分式1.5 可化为一元一次方程的分式方程教学课件(共44张)
文档属性
| 名称 | 湘教版八年级数学上册第一章分式1.5 可化为一元一次方程的分式方程教学课件(共44张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-09 07:07:30 | ||
图片预览










文档简介
(共44张PPT)
可化为一元一次方程的
分式方程
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
甲、乙两名同学同时从学校出发,去15千米外的景区游玩,甲比乙每小时多行1千米,结果比乙早到半小时,甲、乙两名同学每小时各行多少千米?设甲同学每小时行千米,你能列出相应的方程吗?
解:根据题意得:
新课导入
这个方程是我们以前学过的方程吗?它与一元一次方程有什么区别呢?今天就让我们一起探究诸如上面所提到的“特殊的一元一次方程”。
02 新知探究
新知探究
分式方程的概念
定义:
此方程的分母中含有未知数x,像这样分母中含未知数的方程叫做分式方程.
新知探究
练一练
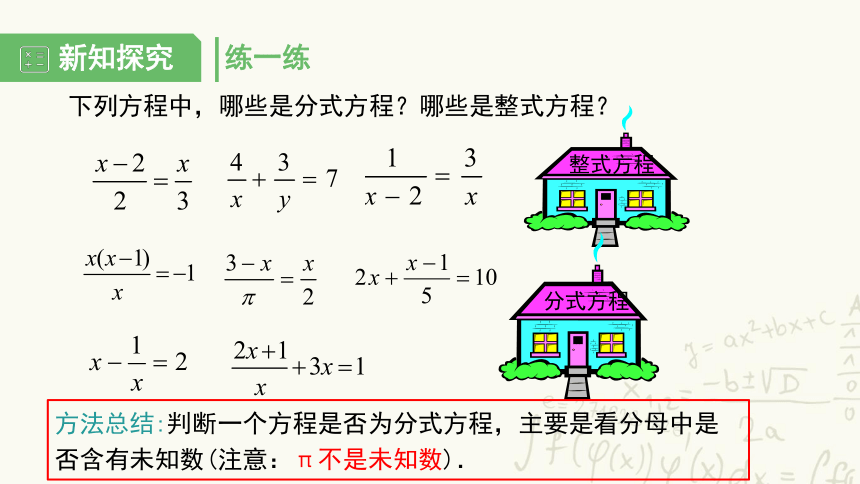
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
方法总结:判断一个方程是否为分式方程,主要是看分母中是否含有未知数(注意:π不是未知数).
新知探究
分式方程的解法
你能试着解这个分式方程吗?
(1)如何把它转化为整式方程呢?
(2)怎样去分母?
(3)在方程两边乘什么样的式子才能把每一个分母都约去?
(4)这样做的依据是什么?
解分式方程最关键的问题是什么?
“去分母”
新知探究
异分母分式的加减
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
新知探究
小归纳
解分式方程的基本思路:是将分式方程化为整式方程,具体做法是“去分母” 即方程两边同乘最简公分母.这也是解分式方程的一般方法.
归纳
新知探究
议一议
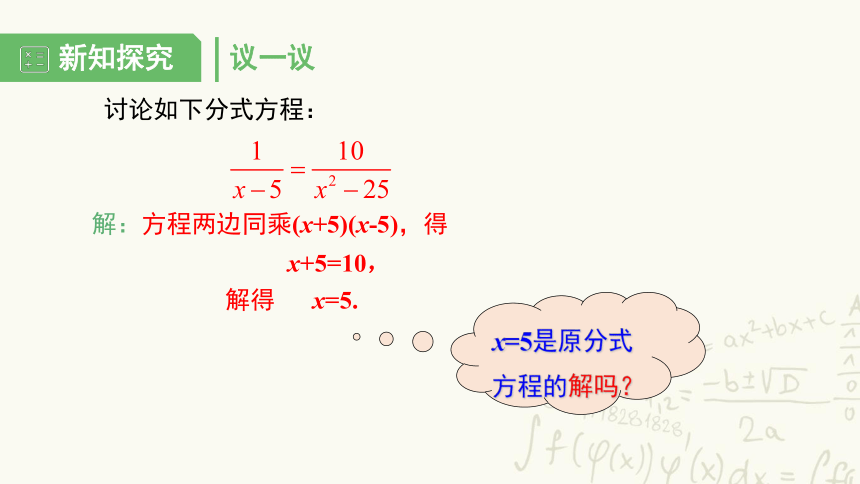
讨论如下分式方程:
解:方程两边同乘(x+5)(x-5),得
x+5=10,
解得 x=5.
x=5是原分式方程的解吗?
新知探究
议一议
检验:将x=5代入原方程中,分母x-5和x2-25的值都为0,相应的分式无意义.因此x=5虽是整式方程x+5=10的解,但不是原分式方程 的解,实际上,这个分式方程无解.
新知探究
想一想
对于分式方程,为什么有的分式方程去分母后所得整式方程的解就是原分式方程的解,而像 去分母后所得整式方程的解却不是原分式方程的解呢?
真相揭秘:对于方程 分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解.
新知探究
想一想
分式方程解的检验------必不可少的步骤
解分式方程时,去分母后所得整式方程的解有可能使原方程的分母为0,所以分式方程的解必须检验.
检验方法:
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
这个整式方程的解是不是原分式的解呢?
怎样检验?
新知探究
小归纳
“去分母法”解分式方程的步骤
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则须舍去。
4.写出原方程的根.
简记为:“一化二解三检验”.
新知探究
练一练
解方程:
解 :方程两边都乘最简公分母,得
解这个一元一次方程,得 x = -5
检验:把 x=-5 代入原方程的左边和右边,得
因此 x = -5 是原方程的解.
提醒:在去分母,将分式方程转化为整式方程解的过程中出现使最简公分母(或分母)为零的根是增根.
新知探究
小归纳
用框图的方式总结为:
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
新知探究
练一练
若关于x的分式方程 无解,求m的值.
解析:先把分式方程化为整式方程,再分两种情况讨论求解:一元一次方程无解与分式方程有增根.
新知探究
练一练
解:方程两边都乘以(x+2)(x-2),
得2(x+2)+mx=3(x-2),即(m-1)x=-10.
①当m-1=0时,此方程无解,此时m=1;
②方程有增根,则x=2或x=-2,
当x=2时,代入(m-1)x=-10
得(m-1)×2=-10,解得m=-4;
当x=-2时,代入(m-1)x=-10
得(m-1)×(-2)=-10,解得m=6,
∴ m的值是1,-4或6.
新知探究
小归纳
分式方程无解与分式方程有增根所表达的意义是不一样的.分式方程有增根仅仅针对使最简公分母为0的数,分式方程无解不但包括使最简公分母为0的数,而且还包括分式方程化为整式方程后,使整式方程无解的数.
新知探究
分式方程的应用
我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有4种:
(1)行程问题: 路程=速度×时间以及它的两个变式;
(2)数字问题: 在数字问题中要掌握十进制数的表示法;
(3)工程问题: 工作量=工时×工效以及它的两个变式;
(4)利润问题: 批发成本=批发数量×批发价;批发数量=批发成本÷批发价;打折销售价=定价×折数;销售利润=销售收入一批发成本;每本销售利润=定价一批发价;每本打折销售利润=打折销售价一批发价,利润率=利润÷进价。
新知探究
工程问题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
设乙单独完成这项工程需要x天.
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
解:设乙单独 完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以6x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
新知探究
小归纳
新知探究
小归纳
工程问题
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如× ×单独完成需 x(单位时间),则可表示出其工作效率;
3.弄清基本的数量关系.如本题中的“合作的工效=甲乙两队工作效率的和”.
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率,工作时间,工作量;2 指该类问题中的 “两个主人公”如甲队和乙队,或“甲单独和两队合作”;1 指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
新知探究
行程问题
朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车车紧随其后,他们同时出发,当面包车车行驶了200公里时,发现小轿车车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少?
0
180
200
新知探究
行程问题
分析:设小轿车的速度为x千米/小时
列表格如下:
路程 速度 时间
面包车
小轿车
200
x+10
180
x
等量关系:
面包车的时间=小轿车的时间
新知探究
行程问题
解:设小轿车的速度为x千米/小时,则面包车速度为x+10千米/小时,依题意得
解得x=90
经检验,x=90是原方程的解,
且x=90,x+10=100,符合题意.
答:面包车的速度为100千米/小时,
小轿车的速度为90千米/小时.
注意两次检验:
(1)是否是所列方程的解;
(2)是否满足实际意义.
新知探究
小归纳
列分式方程解应用题的一般步骤
1.审:清题意,并设未知数;
2.找:相等关系;
3.列:出方程;
4.解:这个分式方程;
5.验:根(包括两方面 :(1)是否是分式方程的根; (2)是否符合题意);
6.写:答案.
03 典型例题
典型例题
1.下列关于x的方程中,是分式方程的是( )
A. B.
C. D.
D
2. 要把方程 化为整式方程,方程两边可以同乘以( )
A. 3y-6 B. 3y
C. 3 (3y-6) D. 3y (y-2)
D
3. 解分式方程 时,去分母后得到的整式方程是( )
A.2(x-8)+5x=16(x-7) B.2(x-8)+5x=8
C.2(x-8)-5x=16(x-7) D.2(x-8)-5x=8
A
4.若关于x的分式方程 无解,则m的值为 ( )
A.-1,5 B.1
C.-1.5或2 D.-0.5或-1.5
D
典型例题
5.解方程:
解: 方程两边乘x(x-3),得
2x=3x-9.
解得
x=9.
检验:当x=9时,x(x-3) ≠0.
所以,原分式方程的解为x=9.
典型例题
6.解方程
解: 方程两边乘(x-1)(x+2),得
x(x+2)-(x-1)(x+2)=3.
解得
x=1.
检验:当x=1时, (x-1)(x+2) =0, 因此x=1不是原分式方程的解.
所以,原分式方程无解.
典型例题
7. 解方程:
解:去分母,得
解得
检验:把 代入
所以原方程的解为
典型例题
04 拓展提高
拓展提高
1. 若关于x的方程 有增根,求m的值.
解:方程两边同乘以x-2,
得2-x+m=2x-4,
合并同类项,得3x=6+m,
∴m=3x-6.
∵该分式方程有增根,
∴x=2,
∴m=0.
05 课堂小结
课堂小结
分式
方程
定义
步骤
(去分母法)
注意
分母中含有未知数的方程叫做分式方程
一化(分式方程转化为整式方程);
二解(整式方程);
三检验(代入最简公分母看是否为零)
(1)去分母时,原方程的整式部分漏乘.
(2)约去分母后,分子是多项式时,没有添括号.(因分数线有括号的作用)
(3)忘记检验
课堂小结
分式方程的应用
类型
行程问题、工程问题、数字问题、顺逆问题、利润问题等
步骤
一审二设三找四列五解六验七写
方法
321法
06 作业布置
完成课本习题 1.5 A、B组
作业布置
谢 谢 观 看
可化为一元一次方程的
分式方程
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
甲、乙两名同学同时从学校出发,去15千米外的景区游玩,甲比乙每小时多行1千米,结果比乙早到半小时,甲、乙两名同学每小时各行多少千米?设甲同学每小时行千米,你能列出相应的方程吗?
解:根据题意得:
新课导入
这个方程是我们以前学过的方程吗?它与一元一次方程有什么区别呢?今天就让我们一起探究诸如上面所提到的“特殊的一元一次方程”。
02 新知探究
新知探究
分式方程的概念
定义:
此方程的分母中含有未知数x,像这样分母中含未知数的方程叫做分式方程.
新知探究
练一练
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
方法总结:判断一个方程是否为分式方程,主要是看分母中是否含有未知数(注意:π不是未知数).
新知探究
分式方程的解法
你能试着解这个分式方程吗?
(1)如何把它转化为整式方程呢?
(2)怎样去分母?
(3)在方程两边乘什么样的式子才能把每一个分母都约去?
(4)这样做的依据是什么?
解分式方程最关键的问题是什么?
“去分母”
新知探究
异分母分式的加减
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
新知探究
小归纳
解分式方程的基本思路:是将分式方程化为整式方程,具体做法是“去分母” 即方程两边同乘最简公分母.这也是解分式方程的一般方法.
归纳
新知探究
议一议
讨论如下分式方程:
解:方程两边同乘(x+5)(x-5),得
x+5=10,
解得 x=5.
x=5是原分式方程的解吗?
新知探究
议一议
检验:将x=5代入原方程中,分母x-5和x2-25的值都为0,相应的分式无意义.因此x=5虽是整式方程x+5=10的解,但不是原分式方程 的解,实际上,这个分式方程无解.
新知探究
想一想
对于分式方程,为什么有的分式方程去分母后所得整式方程的解就是原分式方程的解,而像 去分母后所得整式方程的解却不是原分式方程的解呢?
真相揭秘:对于方程 分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解.
新知探究
想一想
分式方程解的检验------必不可少的步骤
解分式方程时,去分母后所得整式方程的解有可能使原方程的分母为0,所以分式方程的解必须检验.
检验方法:
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
这个整式方程的解是不是原分式的解呢?
怎样检验?
新知探究
小归纳
“去分母法”解分式方程的步骤
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则须舍去。
4.写出原方程的根.
简记为:“一化二解三检验”.
新知探究
练一练
解方程:
解 :方程两边都乘最简公分母,得
解这个一元一次方程,得 x = -5
检验:把 x=-5 代入原方程的左边和右边,得
因此 x = -5 是原方程的解.
提醒:在去分母,将分式方程转化为整式方程解的过程中出现使最简公分母(或分母)为零的根是增根.
新知探究
小归纳
用框图的方式总结为:
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
新知探究
练一练
若关于x的分式方程 无解,求m的值.
解析:先把分式方程化为整式方程,再分两种情况讨论求解:一元一次方程无解与分式方程有增根.
新知探究
练一练
解:方程两边都乘以(x+2)(x-2),
得2(x+2)+mx=3(x-2),即(m-1)x=-10.
①当m-1=0时,此方程无解,此时m=1;
②方程有增根,则x=2或x=-2,
当x=2时,代入(m-1)x=-10
得(m-1)×2=-10,解得m=-4;
当x=-2时,代入(m-1)x=-10
得(m-1)×(-2)=-10,解得m=6,
∴ m的值是1,-4或6.
新知探究
小归纳
分式方程无解与分式方程有增根所表达的意义是不一样的.分式方程有增根仅仅针对使最简公分母为0的数,分式方程无解不但包括使最简公分母为0的数,而且还包括分式方程化为整式方程后,使整式方程无解的数.
新知探究
分式方程的应用
我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有4种:
(1)行程问题: 路程=速度×时间以及它的两个变式;
(2)数字问题: 在数字问题中要掌握十进制数的表示法;
(3)工程问题: 工作量=工时×工效以及它的两个变式;
(4)利润问题: 批发成本=批发数量×批发价;批发数量=批发成本÷批发价;打折销售价=定价×折数;销售利润=销售收入一批发成本;每本销售利润=定价一批发价;每本打折销售利润=打折销售价一批发价,利润率=利润÷进价。
新知探究
工程问题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
设乙单独完成这项工程需要x天.
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
解:设乙单独 完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以6x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
新知探究
小归纳
新知探究
小归纳
工程问题
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如× ×单独完成需 x(单位时间),则可表示出其工作效率;
3.弄清基本的数量关系.如本题中的“合作的工效=甲乙两队工作效率的和”.
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率,工作时间,工作量;2 指该类问题中的 “两个主人公”如甲队和乙队,或“甲单独和两队合作”;1 指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
新知探究
行程问题
朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车车紧随其后,他们同时出发,当面包车车行驶了200公里时,发现小轿车车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少?
0
180
200
新知探究
行程问题
分析:设小轿车的速度为x千米/小时
列表格如下:
路程 速度 时间
面包车
小轿车
200
x+10
180
x
等量关系:
面包车的时间=小轿车的时间
新知探究
行程问题
解:设小轿车的速度为x千米/小时,则面包车速度为x+10千米/小时,依题意得
解得x=90
经检验,x=90是原方程的解,
且x=90,x+10=100,符合题意.
答:面包车的速度为100千米/小时,
小轿车的速度为90千米/小时.
注意两次检验:
(1)是否是所列方程的解;
(2)是否满足实际意义.
新知探究
小归纳
列分式方程解应用题的一般步骤
1.审:清题意,并设未知数;
2.找:相等关系;
3.列:出方程;
4.解:这个分式方程;
5.验:根(包括两方面 :(1)是否是分式方程的根; (2)是否符合题意);
6.写:答案.
03 典型例题
典型例题
1.下列关于x的方程中,是分式方程的是( )
A. B.
C. D.
D
2. 要把方程 化为整式方程,方程两边可以同乘以( )
A. 3y-6 B. 3y
C. 3 (3y-6) D. 3y (y-2)
D
3. 解分式方程 时,去分母后得到的整式方程是( )
A.2(x-8)+5x=16(x-7) B.2(x-8)+5x=8
C.2(x-8)-5x=16(x-7) D.2(x-8)-5x=8
A
4.若关于x的分式方程 无解,则m的值为 ( )
A.-1,5 B.1
C.-1.5或2 D.-0.5或-1.5
D
典型例题
5.解方程:
解: 方程两边乘x(x-3),得
2x=3x-9.
解得
x=9.
检验:当x=9时,x(x-3) ≠0.
所以,原分式方程的解为x=9.
典型例题
6.解方程
解: 方程两边乘(x-1)(x+2),得
x(x+2)-(x-1)(x+2)=3.
解得
x=1.
检验:当x=1时, (x-1)(x+2) =0, 因此x=1不是原分式方程的解.
所以,原分式方程无解.
典型例题
7. 解方程:
解:去分母,得
解得
检验:把 代入
所以原方程的解为
典型例题
04 拓展提高
拓展提高
1. 若关于x的方程 有增根,求m的值.
解:方程两边同乘以x-2,
得2-x+m=2x-4,
合并同类项,得3x=6+m,
∴m=3x-6.
∵该分式方程有增根,
∴x=2,
∴m=0.
05 课堂小结
课堂小结
分式
方程
定义
步骤
(去分母法)
注意
分母中含有未知数的方程叫做分式方程
一化(分式方程转化为整式方程);
二解(整式方程);
三检验(代入最简公分母看是否为零)
(1)去分母时,原方程的整式部分漏乘.
(2)约去分母后,分子是多项式时,没有添括号.(因分数线有括号的作用)
(3)忘记检验
课堂小结
分式方程的应用
类型
行程问题、工程问题、数字问题、顺逆问题、利润问题等
步骤
一审二设三找四列五解六验七写
方法
321法
06 作业布置
完成课本习题 1.5 A、B组
作业布置
谢 谢 观 看
同课章节目录
