高中数学必修5人教版:3.3.2 简单线性规划问题第3课时教案
文档属性
| 名称 | 高中数学必修5人教版:3.3.2 简单线性规划问题第3课时教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-11 00:00:00 | ||
图片预览

文档简介
3.3.2 简单线性规划问题
教学目标
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;?
2.运用线性规划问题的图解法,并能应用它解决一些简单的实际问题.
教学重点:用图解法解决简单的线性规划问题
教学难点:准确求得线性规划问题的最优解
教学过程
第3课时?
导入新课
师 前面我们已经学习了
用图解法解决简单的线性规划问题的基本步骤以及以实际问题为背景的线性规划问题其求解的格式与步骤.这节课我们继续来看它们的实际应用问题.?
推进新课?
师 【例5】 营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪.1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg 脂肪,花费28元;而1kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元.为了满足营养学家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B各多少克??
师 分析:将已知数据列成下表:
食物/kg
碳水化合物/kg
蛋白质/kg
脂肪/kg
A
0.105
0.07
0.14
B
0.105
0.14
0.07
若设每天食用x kg食物A,y kg 食物B,总成本为z,如何列式??
生 由题设条件列出约束条件
其目标函数z=28x+21y.?
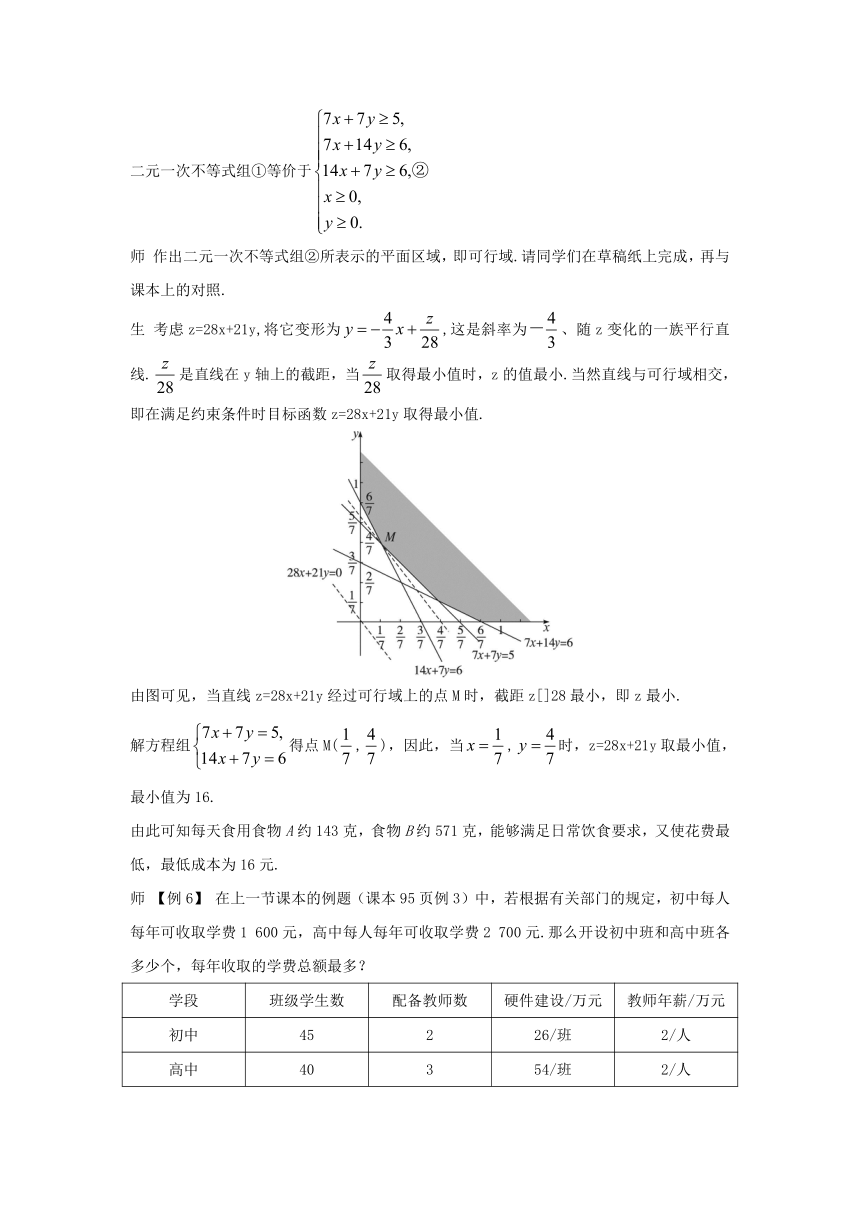
二元一次不等式组①等价于
师 作出二元一次不等式组②所表示的平面区域,即可行域.请同学们在草稿纸上完成,再与课本上的对照.?
生 考虑z=28x+21y,将它变形为,这是斜率为、随z变化的一族平行直线.是直线在y轴上的截距,当取得最小值时,z的值最小.当然直线与可行域相交,即在满足约束条件时目标函数z=28x+21y取得最小值.?
由图可见,当直线z=28x+21y经过可行域上的点M时,截距z[]28最小,即z最小.?
解方程组得点M(,),因此,当,时,z=28x+21y取最小值,最小值为16.?
由此可知每天食用食物A约143克,食物B约571克,能够满足日常饮食要求,又使花费最低,最低成本为16元.?
师 【例6】 在上一节课本的例题(课本95页例3)中,若根据有关部门的规定,初中每人每年可收取学费1 600元,高中每人每年可收取学费2 700元.那么开设初中班和高中班各多少个,每年收取的学费总额最多?
学段
班级学生数
配备教师数
硬件建设/万元
教师年薪/万元
初中
45
2
26/班
2/人
高中
40
3
54/班
2/人
师 由前面内容知若设开设初中班x个,高中班y个,收取的学费总额为z万元,?
此时,目标函数z=0.16×45x+0.27×40y,可行域如下图?
把z=7.2x+10.8y变形为,得到斜率为-,在y轴上截距为,随z变化的一组平行直线.?
由图可以看出,当直线z=7.2x+10.8y经过可行域上的点M时,截距最大,即z最大.?
解方程组得点M(20,10),因此,当x=20,y=10时,z=7.2x+10.8y取最大值,最大值为252.?
由此可知开设20个初中班和10个高中班时,每年收取的学费总额最多,为252万元.?
师 【例7】 在上一节例4中(课本96页例4),若生产1车皮甲种肥料,产生的利润为10 000元,若生产1车皮乙种肥料,产生的利润为5 000元,那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润??
生 若设生产x车皮甲种肥料,y车皮乙种肥料,能够产生的利润z万元.目标函数 z= x+0.5y,可行域如下图:?
把z=x+0.5y变形为y=-2x+2z,得到斜率为-2,在y轴上截距为2z,随z变化的一组平行直线.由图可以看出,当直线y=-2x+2z经过可行域上的点M时,截距2z最大,即z最大.?
解方程组得点M(2,2),因此当x=2,y=2时,z=x+0.5y取最大值,最大值为3.?
由此可见,生产甲、乙两种肥料各2车皮,能够产生最大的利润,最大利润为3万元.?
[教师精讲]?
师 以实际问题为背景的线性规划问题其求解的格式与步骤:?
(1)寻找线性约束条件,线性目标函数;?
(2)由二元一次不等式表示的平面区域做出可行域;?
(3)在可行域内求目标函数的最优解.?
当然也要注意问题的实际意义.
课堂小结?
用图解法解决简单的线性规划问题的基本步骤:?
(1)首先,要根据线性约束条件画出可行域(即画出不等式组所表示的公共区域);?
(2)设t=0,画出直线l0;?
(3)观察、分析,平移直线l0,从而找到最优解;?
(4)最后求得目标函数的最大值及最小值.?
以实际问题为背景的线性规划问题其求解的格式与步骤:?
(1)寻找线性约束条件,线性目标函数;?
(2)由二元一次不等式表示的平面区域做出可行域;?
(3)在可行域内求目标函数的最优解.?
当然也要注意问题的实际意义.
布置作业
课本第105页习题3.3 B组1、2、3
教学目标
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;?
2.运用线性规划问题的图解法,并能应用它解决一些简单的实际问题.
教学重点:用图解法解决简单的线性规划问题
教学难点:准确求得线性规划问题的最优解
教学过程
第3课时?
导入新课
师 前面我们已经学习了
用图解法解决简单的线性规划问题的基本步骤以及以实际问题为背景的线性规划问题其求解的格式与步骤.这节课我们继续来看它们的实际应用问题.?
推进新课?
师 【例5】 营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪.1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg 脂肪,花费28元;而1kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元.为了满足营养学家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B各多少克??
师 分析:将已知数据列成下表:
食物/kg
碳水化合物/kg
蛋白质/kg
脂肪/kg
A
0.105
0.07
0.14
B
0.105
0.14
0.07
若设每天食用x kg食物A,y kg 食物B,总成本为z,如何列式??
生 由题设条件列出约束条件
其目标函数z=28x+21y.?
二元一次不等式组①等价于
师 作出二元一次不等式组②所表示的平面区域,即可行域.请同学们在草稿纸上完成,再与课本上的对照.?
生 考虑z=28x+21y,将它变形为,这是斜率为、随z变化的一族平行直线.是直线在y轴上的截距,当取得最小值时,z的值最小.当然直线与可行域相交,即在满足约束条件时目标函数z=28x+21y取得最小值.?
由图可见,当直线z=28x+21y经过可行域上的点M时,截距z[]28最小,即z最小.?
解方程组得点M(,),因此,当,时,z=28x+21y取最小值,最小值为16.?
由此可知每天食用食物A约143克,食物B约571克,能够满足日常饮食要求,又使花费最低,最低成本为16元.?
师 【例6】 在上一节课本的例题(课本95页例3)中,若根据有关部门的规定,初中每人每年可收取学费1 600元,高中每人每年可收取学费2 700元.那么开设初中班和高中班各多少个,每年收取的学费总额最多?
学段
班级学生数
配备教师数
硬件建设/万元
教师年薪/万元
初中
45
2
26/班
2/人
高中
40
3
54/班
2/人
师 由前面内容知若设开设初中班x个,高中班y个,收取的学费总额为z万元,?
此时,目标函数z=0.16×45x+0.27×40y,可行域如下图?
把z=7.2x+10.8y变形为,得到斜率为-,在y轴上截距为,随z变化的一组平行直线.?
由图可以看出,当直线z=7.2x+10.8y经过可行域上的点M时,截距最大,即z最大.?
解方程组得点M(20,10),因此,当x=20,y=10时,z=7.2x+10.8y取最大值,最大值为252.?
由此可知开设20个初中班和10个高中班时,每年收取的学费总额最多,为252万元.?
师 【例7】 在上一节例4中(课本96页例4),若生产1车皮甲种肥料,产生的利润为10 000元,若生产1车皮乙种肥料,产生的利润为5 000元,那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润??
生 若设生产x车皮甲种肥料,y车皮乙种肥料,能够产生的利润z万元.目标函数 z= x+0.5y,可行域如下图:?
把z=x+0.5y变形为y=-2x+2z,得到斜率为-2,在y轴上截距为2z,随z变化的一组平行直线.由图可以看出,当直线y=-2x+2z经过可行域上的点M时,截距2z最大,即z最大.?
解方程组得点M(2,2),因此当x=2,y=2时,z=x+0.5y取最大值,最大值为3.?
由此可见,生产甲、乙两种肥料各2车皮,能够产生最大的利润,最大利润为3万元.?
[教师精讲]?
师 以实际问题为背景的线性规划问题其求解的格式与步骤:?
(1)寻找线性约束条件,线性目标函数;?
(2)由二元一次不等式表示的平面区域做出可行域;?
(3)在可行域内求目标函数的最优解.?
当然也要注意问题的实际意义.
课堂小结?
用图解法解决简单的线性规划问题的基本步骤:?
(1)首先,要根据线性约束条件画出可行域(即画出不等式组所表示的公共区域);?
(2)设t=0,画出直线l0;?
(3)观察、分析,平移直线l0,从而找到最优解;?
(4)最后求得目标函数的最大值及最小值.?
以实际问题为背景的线性规划问题其求解的格式与步骤:?
(1)寻找线性约束条件,线性目标函数;?
(2)由二元一次不等式表示的平面区域做出可行域;?
(3)在可行域内求目标函数的最优解.?
当然也要注意问题的实际意义.
布置作业
课本第105页习题3.3 B组1、2、3
