湘教版七年级数学上册:2.5 第1课时 合并同类项课件(30张PPT)
文档属性
| 名称 | 湘教版七年级数学上册:2.5 第1课时 合并同类项课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-09 00:00:00 | ||
图片预览










文档简介
课件30张PPT。新课标 第2章代数式2.5 第1课时 合并同类项1.理解同类项及合并同类项的概念,会识别同类项.
2.掌握合并同类项法则,能进行同类项的合并.学习目标1.在具体情境中感受合并同类项的必要性,理解合并同类项法则所依据的运算律.(重点)
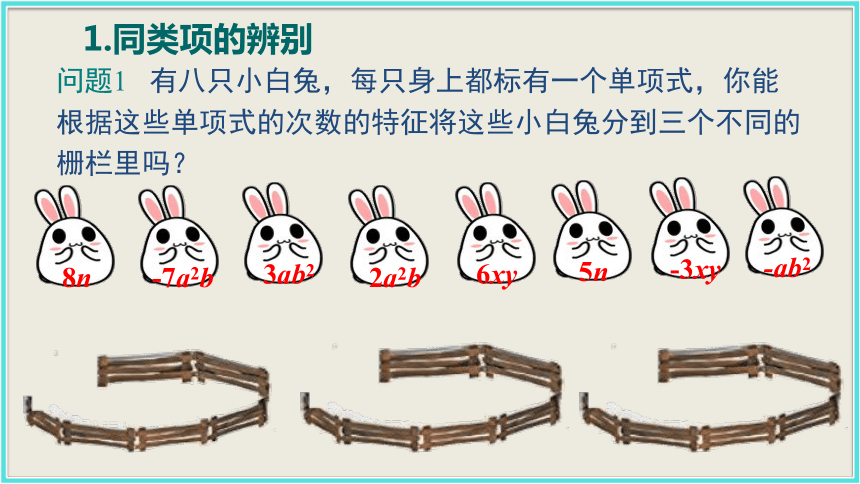
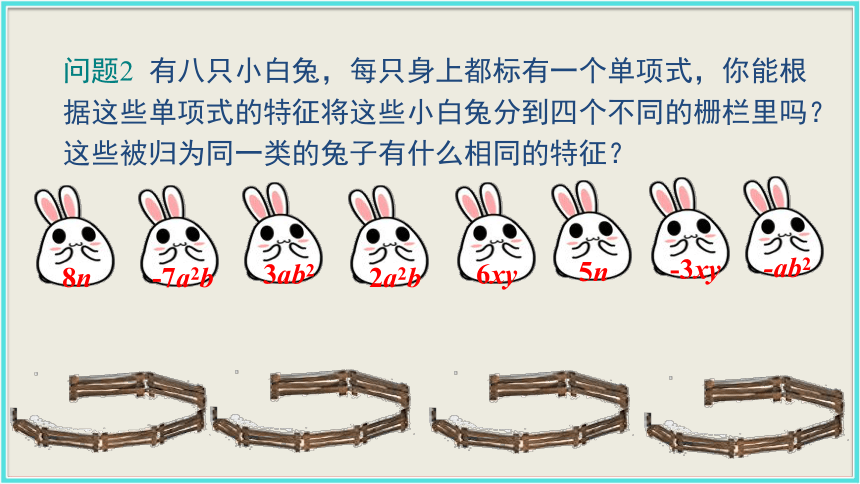
2.了解合并同类项的法则,能进行同类项的合并.(难点)素养提升 生活中,我们常常把具有相同特征的事物归为一类 ,请同学们给下列物品分类.蔬菜水果观察药店药品摆放观察超市货物摆放 如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢?储蓄罐-7a2b问题1 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的次数的特征将这些小白兔分到三个不同的栅栏里吗?8n3ab22a2b6xy5n-3xy-ab21.同类项的辨别-7a2b问题2 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到四个不同的栅栏里吗?这些被归为同一类的兔子有什么相同的特征? 8n3ab22a2b6xy5n-3xy-ab2同类项:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.(1)两个相同:字母相同;相同字母的次数相同; (2)两个无关:与系数大小无关;与字母顺序无关; (3)所有的常数项都是同类项. 说明:知识要点找朋友游戏一游戏二 同类项速配 先判断每一组是否是同类项,若不是的,请为前者配一个.√√3abcx2y××总结归纳(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可. 同类项的判别方法(3)不要忘记几个单独的数也是同类项. 下列式子中是同类项的是 ( )
A.62和x2 B.11abc和9bc
C.3m2n3和-n3m2 D.0.2a2b和ab2解析 根据所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项可得答案.A.62是一个数,x2含有字母且字母指数为2,所以不是同类项,故此选项错误;B.11abc和9bc所含字母不同,所以不是同类项,故此选项错误;C.3m2n3和-n3m2所含字母相同,且字母指数也相同,所以是同类项,故此选项正确;D.0.2a2b和ab2所含字母相同,但每个字母的指数不同,所以不是同类项,故此选项错误.判断两项是否为同类项,一定要严格按照同类项的定义来判断,首先看两项中所含字母是否相同,再看相同字母的指数是否相同,特别注意常数项都是同类项.C1.判断下列各题中的两项是不是同类项.
(1)a2b3与2b3a2;
(2)- x2yz与- xy2z;
(3)x2与32;
(4)-2018与2019.解:(1) a2b3与2b3a2,所含字母相同,相同字母的指数也相同,是同类项. (2)- x2yz与- xy2z,所含字母指数不同,不是同类项. (3)x2与32,所含字母不同,不是同类项. (4)-2018与2019是同类项.练习xxx2+ 3=5=3-a2bca2bca2bc2奇妙的替换你还有其他方法解释吗?2.合并同类项利用乘法分配律可得(2+3)(3-2)= 5x= a2bc把同类项合并成一项叫做合并同类项. 例2. 合并下式中的同类项:
(1) (2)解:(1)(2) 例3. 合并下式中的同类项:
(1)
(2)解:(1)(2)1.将同类项在底下划线标出;2.运用加法的交换律和结合律,把同类项放在一起;3.合并同类项.注意:对于不同的同类项,分别用不同的线标出.“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可. 总结归纳系数相加,字母及其指数不变(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2 下列合并同类项对吗?不对的,说明理由.(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a说一说×√×××√ 你会计算吗?
⑴ 100t-252t ;
⑵ 3a+2b-5a-b ;
⑶ -4ab+8-2b2-9ab-8 .
试一试答案:⑴-152t ; ⑵-2a+b ; ⑶-13ab-2b2.先分组,再合并练一练合并同类项:
(1)6x+2x2-3x+x2+1;
(2)-3ab+7-2a2-9ab-3.解:(1)原式=(6x-3x)+(2x2+x2)+1
=3x+3x2+1(2)原式=(-3ab-9ab)-2a2+(7-3)
=-12ab-2a2+4 例4 (1)求多项式 的值, 其中x = ; (2)求多项式 的值, 其中a= ,b=2,c=-3. 分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.解:(1)
当x = 时,原式= (2)
当a= ,b=2,c=-3时,原式=1.议一议 在不知道a,b的情况下,能否求出“7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2”的值,若能,请求出数值;若不能,请说明理由.解:能.理由如下:
化简7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2
=(7a2-4a2-3a2)+(-5b2+b2+4b2)+(3a2b-3a2b)-2
=-2,
所以无论a,b取任何值,代数式的值都为2. 例5 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克.所以摊主说得没有道理,这样做小明奶奶吃亏了.
1.如果5x2y与xmyn是同类项,那么 m=____,n=____.
2.合并同类项:
(1)-a-a-2a=________.
(2)-xy-5xy+6yx=________.
(3)0.8ab2-a2b+0.2ab2=_______.
3.下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
4.下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x2 1-4a0ab2-a2bCA合并下列各式中的同类项:
5.-7mn+mn+5nm;
6.3a2b-4ab2-4+5a2b+2ab2+7.-mn8a2b-2ab2+3解:(1)由单项式5mxay与-5nx2a-3y是关于x,y的单项式,且它们是同类项,得a=2a-3,解得a=3,所以(7a-22)2019=(7×3-22)2019=(-1)2019=-1.
(2)由5mxay-5nx2a-3y=0,且xy≠0,得5m-5n=0,所以(5m-5n)2018=02018=0.7.已知单项式5mxay与-5nx2a-3y是关于x,y的单项式,且它们是同类项.
(1)求(7a-22)2019的值;
(2)若5mxay-5nx2a-3y=0,且xy≠0,求(5m-5n)2018的值.
合并同类项的方法——“一加二不变”同类项的概念合并同类项
2.掌握合并同类项法则,能进行同类项的合并.学习目标1.在具体情境中感受合并同类项的必要性,理解合并同类项法则所依据的运算律.(重点)
2.了解合并同类项的法则,能进行同类项的合并.(难点)素养提升 生活中,我们常常把具有相同特征的事物归为一类 ,请同学们给下列物品分类.蔬菜水果观察药店药品摆放观察超市货物摆放 如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢?储蓄罐-7a2b问题1 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的次数的特征将这些小白兔分到三个不同的栅栏里吗?8n3ab22a2b6xy5n-3xy-ab21.同类项的辨别-7a2b问题2 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到四个不同的栅栏里吗?这些被归为同一类的兔子有什么相同的特征? 8n3ab22a2b6xy5n-3xy-ab2同类项:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.(1)两个相同:字母相同;相同字母的次数相同; (2)两个无关:与系数大小无关;与字母顺序无关; (3)所有的常数项都是同类项. 说明:知识要点找朋友游戏一游戏二 同类项速配 先判断每一组是否是同类项,若不是的,请为前者配一个.√√3abcx2y××总结归纳(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可. 同类项的判别方法(3)不要忘记几个单独的数也是同类项. 下列式子中是同类项的是 ( )
A.62和x2 B.11abc和9bc
C.3m2n3和-n3m2 D.0.2a2b和ab2解析 根据所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项可得答案.A.62是一个数,x2含有字母且字母指数为2,所以不是同类项,故此选项错误;B.11abc和9bc所含字母不同,所以不是同类项,故此选项错误;C.3m2n3和-n3m2所含字母相同,且字母指数也相同,所以是同类项,故此选项正确;D.0.2a2b和ab2所含字母相同,但每个字母的指数不同,所以不是同类项,故此选项错误.判断两项是否为同类项,一定要严格按照同类项的定义来判断,首先看两项中所含字母是否相同,再看相同字母的指数是否相同,特别注意常数项都是同类项.C1.判断下列各题中的两项是不是同类项.
(1)a2b3与2b3a2;
(2)- x2yz与- xy2z;
(3)x2与32;
(4)-2018与2019.解:(1) a2b3与2b3a2,所含字母相同,相同字母的指数也相同,是同类项. (2)- x2yz与- xy2z,所含字母指数不同,不是同类项. (3)x2与32,所含字母不同,不是同类项. (4)-2018与2019是同类项.练习xxx2+ 3=5=3-a2bca2bca2bc2奇妙的替换你还有其他方法解释吗?2.合并同类项利用乘法分配律可得(2+3)(3-2)= 5x= a2bc把同类项合并成一项叫做合并同类项. 例2. 合并下式中的同类项:
(1) (2)解:(1)(2) 例3. 合并下式中的同类项:
(1)
(2)解:(1)(2)1.将同类项在底下划线标出;2.运用加法的交换律和结合律,把同类项放在一起;3.合并同类项.注意:对于不同的同类项,分别用不同的线标出.“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可. 总结归纳系数相加,字母及其指数不变(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2 下列合并同类项对吗?不对的,说明理由.(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a说一说×√×××√ 你会计算吗?
⑴ 100t-252t ;
⑵ 3a+2b-5a-b ;
⑶ -4ab+8-2b2-9ab-8 .
试一试答案:⑴-152t ; ⑵-2a+b ; ⑶-13ab-2b2.先分组,再合并练一练合并同类项:
(1)6x+2x2-3x+x2+1;
(2)-3ab+7-2a2-9ab-3.解:(1)原式=(6x-3x)+(2x2+x2)+1
=3x+3x2+1(2)原式=(-3ab-9ab)-2a2+(7-3)
=-12ab-2a2+4 例4 (1)求多项式 的值, 其中x = ; (2)求多项式 的值, 其中a= ,b=2,c=-3. 分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.解:(1)
当x = 时,原式= (2)
当a= ,b=2,c=-3时,原式=1.议一议 在不知道a,b的情况下,能否求出“7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2”的值,若能,请求出数值;若不能,请说明理由.解:能.理由如下:
化简7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2
=(7a2-4a2-3a2)+(-5b2+b2+4b2)+(3a2b-3a2b)-2
=-2,
所以无论a,b取任何值,代数式的值都为2. 例5 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克.所以摊主说得没有道理,这样做小明奶奶吃亏了.
1.如果5x2y与xmyn是同类项,那么 m=____,n=____.
2.合并同类项:
(1)-a-a-2a=________.
(2)-xy-5xy+6yx=________.
(3)0.8ab2-a2b+0.2ab2=_______.
3.下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
4.下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x2 1-4a0ab2-a2bCA合并下列各式中的同类项:
5.-7mn+mn+5nm;
6.3a2b-4ab2-4+5a2b+2ab2+7.-mn8a2b-2ab2+3解:(1)由单项式5mxay与-5nx2a-3y是关于x,y的单项式,且它们是同类项,得a=2a-3,解得a=3,所以(7a-22)2019=(7×3-22)2019=(-1)2019=-1.
(2)由5mxay-5nx2a-3y=0,且xy≠0,得5m-5n=0,所以(5m-5n)2018=02018=0.7.已知单项式5mxay与-5nx2a-3y是关于x,y的单项式,且它们是同类项.
(1)求(7a-22)2019的值;
(2)若5mxay-5nx2a-3y=0,且xy≠0,求(5m-5n)2018的值.
合并同类项的方法——“一加二不变”同类项的概念合并同类项
同课章节目录
