湘教版七年级数学上册:3.2 等式的性质课件(35张PPT)
文档属性
| 名称 | 湘教版七年级数学上册:3.2 等式的性质课件(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-09 15:36:55 | ||
图片预览











文档简介
课件35张PPT。新课标 第3章一元一次方程3.2 等式的性质学习目标1.借助天平理解等式的性质.(重点)
2.能利用等式性质解简单的一元一次方程.(难点)素养提升1.了解等式的实际意义,体会数学与现实生活的密切关系.
2.掌握等式的两个性质,并会利用等式的性质解简单的一元一次方程.设问导入(1)如果:七年级(1)班的学生人数=七年级(2)班的学生人数.
现在每班增加2名学生,那么七年级(1)班与七年级(2)班的学生人数相等吗?
如果每班减少3名学生,那么这两个班的学生人数还相等吗?
(2)如果:甲筐米的质量=乙筐米的质量
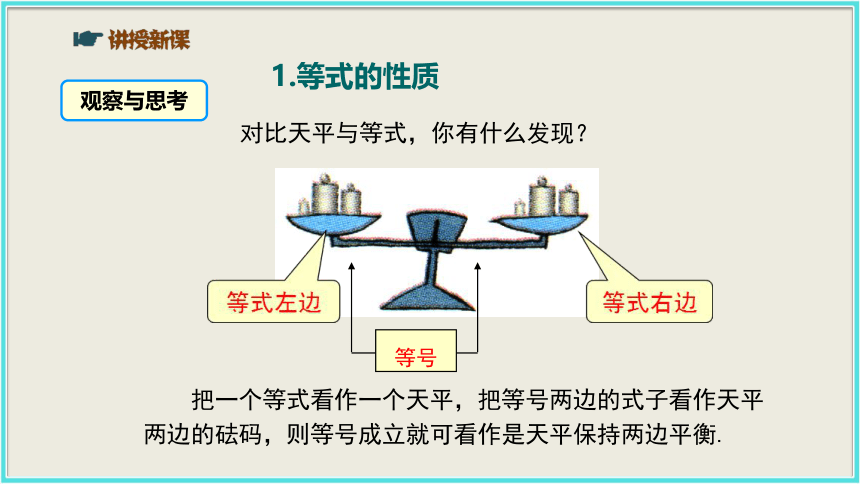
现在将甲、乙两筐米分别倒出一半,那么甲、乙两筐剩下的米的质量相等吗?情境引入思考:要让天平平衡应该满足什么条件?1.等式的性质观察与思考对比天平与等式,你有什么发现? 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.观察天平有什么特性?天平两边同时加入相同质量的砝码天平仍然平衡天平两边同时拿去相同质量的砝码天平仍然平衡由天平性质看等式的性质1天平两边同时天平仍然平衡加入拿去相同质量的砝码相同的数(或式子) 等式两边同时加上减去等式仍然成立换言之,
等式两边加 (或减) 同一个数 (或式子),所得结果仍是等式.如果a=b,那么a±c=b±c.要点归纳等式的性质1由天平性质看等式的性质2
等式两边乘同一个数 (或式),或除以同一个不为0的数(或式),所得结果仍是等式.等式的性质2知识要点典例精析(1)如果a+2 = b+7,那么a= ;解:因为a+2=b+7 ,由等式性质1可知,
等式两边都减去2,得
a + 2 - 2 = b + 7 -2,
即 a = b + 5 .b + 5 (2)如果3x = 9y,那么 x= ;解:因为3x=9y,由等式性质2可知,
等式两边都除以3,得
,
即 x = 3y. 3y解:因为 ,由等式性质2可知,
等式两边都乘6,得
即 3a = 2b .2b 典例精析下列运用等式性质的变形,正确的是 ( )
A.如果a=b,那么a+c=b-c
B.如果 ,那么a=b
C.如果a=b,那么
D.如果a=3,那么a2=3a2解析:选项A,利用等式性质1,两边都加c,得到a+c=b+c,所以A不成立;选项B,利用等式性质2,两边都乘c,得到a=b,所以B成立;选项C,若c=0,则=不成立,所以C不成立;选项D,因为a2=9,3a2=27,所以a2≠3a2,所以D不成立.故选B.利用等式性质进行变形时:(1)两边必须同时进行完全相同的四则运算,并且除以同一个数时,这个数不能为0.(2)熟练掌握互为相反数的两个数之间的关系和互为倒数的两个数之间的关系,有助于等式的灵活变形.B(2018·深圳模拟)将等式3a-2b=2a-2b变形,过程如下:
因为3a-2b=2a-2b,
所以3a=2a(第一步),
所以3=2(第二步).
上述过程中,第一步的根据是 ,第二步得出了明显错误的结论,其原因是 .?练习等式的基本性质1没有考虑a=0的情况2.利用等式的性质求值例3 利用等式的性质,求出下列方程中x的值:
(1) x + 7 = 26 解:得 方程两边同时减去7,x + 7 = 26 于是 x= 19.提示:利用等式的性质把原方程“化归”为“ x=a ”的形式即可. (2) -5x = 20 化简,得 x=-4.-5x÷(-5)= 20 ÷(-5)1.下列等式的变形中,不正确的是 ( )
A.若x=y,则x+5=y+5
B.若 (a≠0),则x=y
C.若-3x=-3y,则x=y
D.若mx=my,则x=yD2. 如果2x-5=6,那么2x= ,其根据是 .
x= ,其根据是 .?3.用等式的性质解方程2- x=3的步骤如下:
两边都减去 ,得2-x-2=3-2,?化简,得 = ,?
两边同乘-4,得x= ,?
检验:将x=-4代入方程2- x=3中,得:左边=2- ×(-4)= ,因为方程的 = .?
所以x=-4是原方程的解.11两边同加上5两边同除以221-43左边 右边4.已知2x2+3x=7,求-4x2-6x+2033的值.解:由2x2+3x=7,根据等式性质2,可得-4x2-6x=-14,
根据等式性质1,可得-4x2-6x+2033=-14+2033=2019.5.利用等式的性质求未知数的值,并检验.等式的
性质性质1性质2应用运用等式的性质把方程“化归”为最简的形式 x = a
2.能利用等式性质解简单的一元一次方程.(难点)素养提升1.了解等式的实际意义,体会数学与现实生活的密切关系.
2.掌握等式的两个性质,并会利用等式的性质解简单的一元一次方程.设问导入(1)如果:七年级(1)班的学生人数=七年级(2)班的学生人数.
现在每班增加2名学生,那么七年级(1)班与七年级(2)班的学生人数相等吗?
如果每班减少3名学生,那么这两个班的学生人数还相等吗?
(2)如果:甲筐米的质量=乙筐米的质量
现在将甲、乙两筐米分别倒出一半,那么甲、乙两筐剩下的米的质量相等吗?情境引入思考:要让天平平衡应该满足什么条件?1.等式的性质观察与思考对比天平与等式,你有什么发现? 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.观察天平有什么特性?天平两边同时加入相同质量的砝码天平仍然平衡天平两边同时拿去相同质量的砝码天平仍然平衡由天平性质看等式的性质1天平两边同时天平仍然平衡加入拿去相同质量的砝码相同的数(或式子) 等式两边同时加上减去等式仍然成立换言之,
等式两边加 (或减) 同一个数 (或式子),所得结果仍是等式.如果a=b,那么a±c=b±c.要点归纳等式的性质1由天平性质看等式的性质2
等式两边乘同一个数 (或式),或除以同一个不为0的数(或式),所得结果仍是等式.等式的性质2知识要点典例精析(1)如果a+2 = b+7,那么a= ;解:因为a+2=b+7 ,由等式性质1可知,
等式两边都减去2,得
a + 2 - 2 = b + 7 -2,
即 a = b + 5 .b + 5 (2)如果3x = 9y,那么 x= ;解:因为3x=9y,由等式性质2可知,
等式两边都除以3,得
,
即 x = 3y. 3y解:因为 ,由等式性质2可知,
等式两边都乘6,得
即 3a = 2b .2b 典例精析下列运用等式性质的变形,正确的是 ( )
A.如果a=b,那么a+c=b-c
B.如果 ,那么a=b
C.如果a=b,那么
D.如果a=3,那么a2=3a2解析:选项A,利用等式性质1,两边都加c,得到a+c=b+c,所以A不成立;选项B,利用等式性质2,两边都乘c,得到a=b,所以B成立;选项C,若c=0,则=不成立,所以C不成立;选项D,因为a2=9,3a2=27,所以a2≠3a2,所以D不成立.故选B.利用等式性质进行变形时:(1)两边必须同时进行完全相同的四则运算,并且除以同一个数时,这个数不能为0.(2)熟练掌握互为相反数的两个数之间的关系和互为倒数的两个数之间的关系,有助于等式的灵活变形.B(2018·深圳模拟)将等式3a-2b=2a-2b变形,过程如下:
因为3a-2b=2a-2b,
所以3a=2a(第一步),
所以3=2(第二步).
上述过程中,第一步的根据是 ,第二步得出了明显错误的结论,其原因是 .?练习等式的基本性质1没有考虑a=0的情况2.利用等式的性质求值例3 利用等式的性质,求出下列方程中x的值:
(1) x + 7 = 26 解:得 方程两边同时减去7,x + 7 = 26 于是 x= 19.提示:利用等式的性质把原方程“化归”为“ x=a ”的形式即可. (2) -5x = 20 化简,得 x=-4.-5x÷(-5)= 20 ÷(-5)1.下列等式的变形中,不正确的是 ( )
A.若x=y,则x+5=y+5
B.若 (a≠0),则x=y
C.若-3x=-3y,则x=y
D.若mx=my,则x=yD2. 如果2x-5=6,那么2x= ,其根据是 .
x= ,其根据是 .?3.用等式的性质解方程2- x=3的步骤如下:
两边都减去 ,得2-x-2=3-2,?化简,得 = ,?
两边同乘-4,得x= ,?
检验:将x=-4代入方程2- x=3中,得:左边=2- ×(-4)= ,因为方程的 = .?
所以x=-4是原方程的解.11两边同加上5两边同除以221-43左边 右边4.已知2x2+3x=7,求-4x2-6x+2033的值.解:由2x2+3x=7,根据等式性质2,可得-4x2-6x=-14,
根据等式性质1,可得-4x2-6x+2033=-14+2033=2019.5.利用等式的性质求未知数的值,并检验.等式的
性质性质1性质2应用运用等式的性质把方程“化归”为最简的形式 x = a
同课章节目录
