湘教版七年级数学上册4.1 几何图形课件(51张ppt)
文档属性
| 名称 | 湘教版七年级数学上册4.1 几何图形课件(51张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-09 23:20:14 | ||
图片预览









文档简介
课件51张PPT。新课标 第4章图形的认识4.1 几何图形学习目标1.能从简单实物的外形中抽象出几何图形,认识平面图形和立体图形;(重点)
2.掌握从不同的方向看立体图形得到的平面图形以及常见立体图形的展开图.(难点)素养提升1.了解几何图形、立体图形、平面图形的概念.
2.认识柱体、锥体与球等立体图形,并对具体事物中的图形进行识别或判断.
3.探索立体图形与平面图形之间的区别与联系,并能正确区分立体图形与平面图形. 从城市建筑到乡村住宅,从立交桥到交通标志,从剪纸艺术到城市雕塑,从动物形态到申奥标志……图形世界是多姿多彩的!
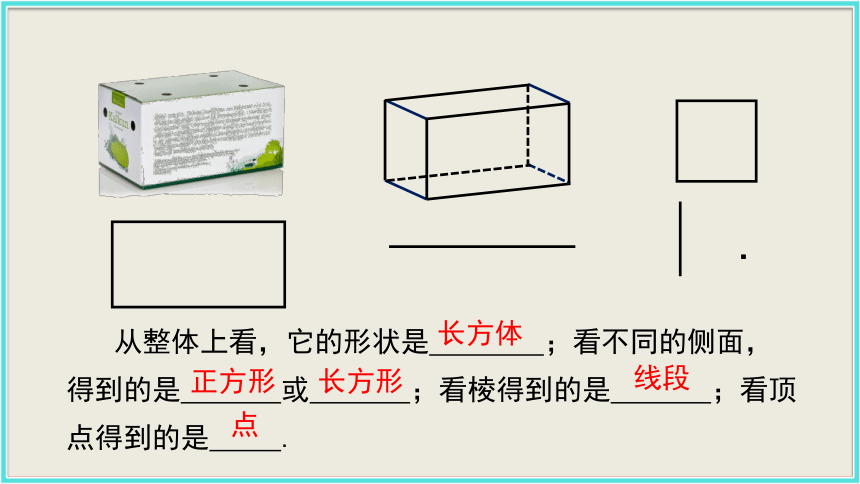
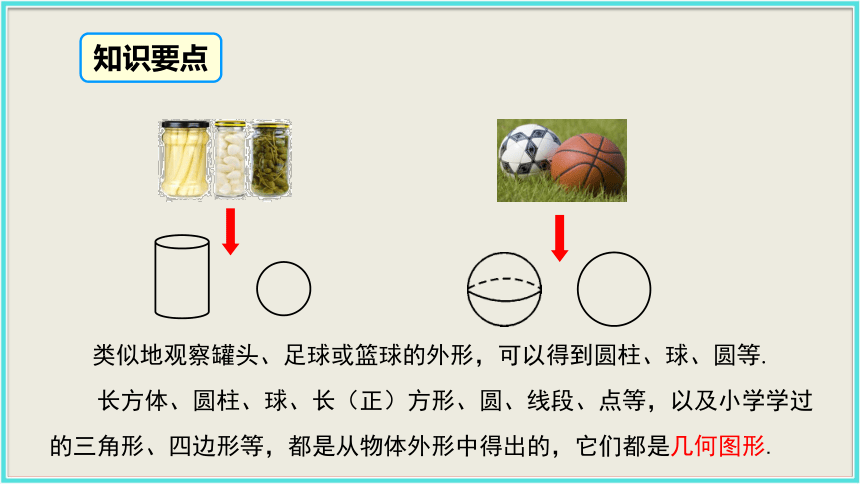
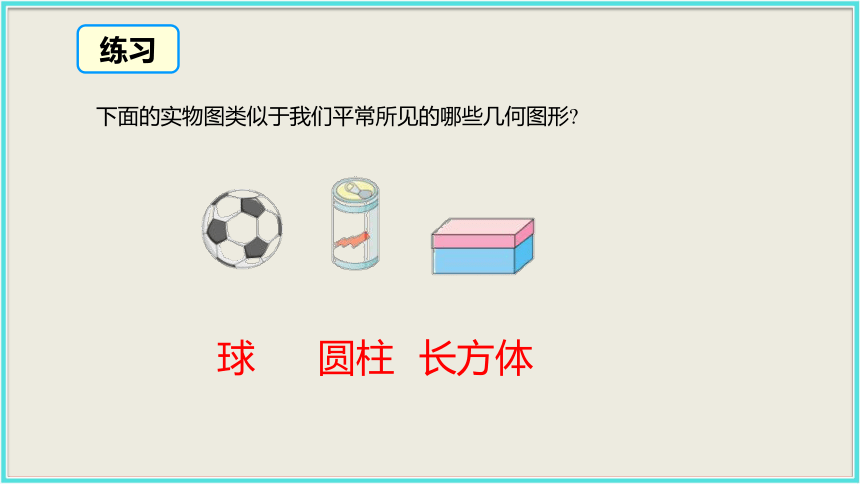
物体的形状、大小和位置关系是几何研究的内容.1.几何图形观察这个纸盒,从中可以看出哪些你熟悉的图形?合作探究看整体看侧面看上面看棱看顶点. 从整体上看,它的形状是 ;看不同的侧面,得到的是 或 ;看棱得到的是 ;看顶点得到的是 .长方体正方形长方形线段点 长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学过的三角形、四边形等,都是从物体外形中得出的,它们都是几何图形. 类似地观察罐头、足球或篮球的外形,可以得到圆柱、球、圆等.知识要点典例精析解析:埃及金字塔的底面是多边形,侧面是有公共顶点的三角形,所以它类似于棱锥. 实物图类似于哪种几何图形,首先要多观察,然后与我们平时所见的几何图形比较即可得出结论.C下面的实物图类似于我们平常所见的哪些几何图形?练习球圆柱长方体2. 立体图形合作探究 生活中你会常见很多实物,由下列实物能想 象出你熟悉的几何图形吗?
(1)文具盒 (2)魔方 (3)笔筒 (4)足球 (5)漏斗长方体正方体圆柱球圆锥 这些几何图形的各部分不都在同一平面内,它们是立体图形.正方体长方体棱柱圆柱棱锥圆锥球体常见的立体图形思考:(1) 棱锥与棱柱的区别是什么?
(2) 圆锥与圆柱的区别是什么? 典例精析解析:熟记一些常见的立体图形即可判断.
解 正方体、长方体、棱柱、圆柱、圆锥、棱锥、球.(1)注意圆柱与棱柱的区别:圆柱的底面是圆,棱柱的底面是多边形,圆柱的侧面是曲面,棱柱的侧面是平行四边形.(2)棱柱与棱锥的区别:棱锥的底面是多边形,圆锥的底面是圆,棱锥的侧面是三角形,圆锥的侧面是曲面.说出下列立体图形(如图4 - 2所示)的名称.图4 - 22.观察小明的房间,说说你能看到哪些立体图形?练习球、圆柱、长方体、正方体、棱柱、圆锥.3.平面图形 说一说下面这些几何图形又有什么共同特点? 这些几何图形的各部分都在同一平面内,它们是平面图形. 观察与思考 下面各图中包含哪些简单的平面图形?请再举出一些平面图形的例子.典例精析解析:选项A中,球、圆锥是立体图形,故A错误;选项B中,棱锥、棱柱是立体图形,故B错误;选项D中,长方体是立体图形,故D错误.图形的各部分都在同一平面内的图形叫做平面图形.熟练掌握平面图形与立体图形的区别是解题的关键.下列各组图形中都是平面图形的是 ( )
A.三角形、圆、球、圆锥 B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆 D.点、角、线段、长方体C如图所示的是一座房子的平面图,组成这幅图的几何图形有 .?练习三角形、正方形、长方形、梯形.4. 几何图形的构成元素问题: 这些几何体是由什么围成的吗?它们有什么不同吗?合作探究它们都有表面,包围着体的是面.曲面曲面平面平面观察下列图形,你看到了哪些面?面有平的面和曲的面两种下列几何体的面哪些是平的?哪些是曲的?立方体长方体圆柱体圆锥体球体3.几何图形都是由点、线、面、体组成的.1.面与面相交形成线;2.线与线相交得到点;观察发现这可以说成:点动成线. 笔尖可以看作是一个点,这个点在纸上运动时,形成了什么?问题:深入探究你能举出其他“点动成线”的实例吗?线动成面实际生活中的“线动成面”面动成体5.从不同方向看物体及立体图形的展开与折叠合作探究从不同的方向看下面的立体图形,你会得到什么?从正面看从左面看从上面看圆柱体从正面看从左面看从上面看圆锥从正面看从左面看从上面看四棱锥从正面看从左面看从上面看三棱柱 将一个正方体的表面沿某些棱剪开,能展开成什么样的图形?圆柱体、圆锥体展开呢?想一想圆柱圆锥说一说:下面图形是一些立体图形的表面展开图,你能说出这些立体图形的名字吗?典例精析(2018·河南中考)某正方体的每个面上都有一个汉字,如图所示的是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是 ( )
A.厉 B.害 C.了 D.我D解析:正方体的表面展开图中,相对的面之间一定相隔一个正方形,根据这一特点作答.“我”与“国”相对;“厉”与“了”相对;“害”与“的”相对.(2018·陕西中考)如图所示的是一个几何体的表面展开图,则该几何体是 ( )
?
A.正方体 B.长方体
C.三棱柱 D.四棱锥练习C1.下列图形不是立体图形的是 ( )
A.球 B.圆柱 C.圆锥 D.圆D2.(2019·山东潍坊期末)如图4 - 16所示,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,则这个平面图形是图4 - 17中的 ( )图4 - 17B3.如图4 - 18所示的是一个立方体纸盒的展开图,使展开图折叠成正方体后相对面上的两个数互为相反数,则a= ;b= ;c= .?图4 - 18-2-714.分别画出如图4 - 19所示的圆柱、圆锥及球从正面、左面、上面看到的图形.
图4 - 19从正面看从左边看从上面看5.如图4 - 21所示的都是平面图形.图4 - 21(1)每个图形各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入表格中.(2)根据(1)中的结论,推断出一个平面图形的顶点数、边数、区域数之间的关系.812569410156由(1)中的结论得:边数-顶点数+1=区域数.几何图形 立体图形的展开与折叠
2.掌握从不同的方向看立体图形得到的平面图形以及常见立体图形的展开图.(难点)素养提升1.了解几何图形、立体图形、平面图形的概念.
2.认识柱体、锥体与球等立体图形,并对具体事物中的图形进行识别或判断.
3.探索立体图形与平面图形之间的区别与联系,并能正确区分立体图形与平面图形. 从城市建筑到乡村住宅,从立交桥到交通标志,从剪纸艺术到城市雕塑,从动物形态到申奥标志……图形世界是多姿多彩的!
物体的形状、大小和位置关系是几何研究的内容.1.几何图形观察这个纸盒,从中可以看出哪些你熟悉的图形?合作探究看整体看侧面看上面看棱看顶点. 从整体上看,它的形状是 ;看不同的侧面,得到的是 或 ;看棱得到的是 ;看顶点得到的是 .长方体正方形长方形线段点 长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学过的三角形、四边形等,都是从物体外形中得出的,它们都是几何图形. 类似地观察罐头、足球或篮球的外形,可以得到圆柱、球、圆等.知识要点典例精析解析:埃及金字塔的底面是多边形,侧面是有公共顶点的三角形,所以它类似于棱锥. 实物图类似于哪种几何图形,首先要多观察,然后与我们平时所见的几何图形比较即可得出结论.C下面的实物图类似于我们平常所见的哪些几何图形?练习球圆柱长方体2. 立体图形合作探究 生活中你会常见很多实物,由下列实物能想 象出你熟悉的几何图形吗?
(1)文具盒 (2)魔方 (3)笔筒 (4)足球 (5)漏斗长方体正方体圆柱球圆锥 这些几何图形的各部分不都在同一平面内,它们是立体图形.正方体长方体棱柱圆柱棱锥圆锥球体常见的立体图形思考:(1) 棱锥与棱柱的区别是什么?
(2) 圆锥与圆柱的区别是什么? 典例精析解析:熟记一些常见的立体图形即可判断.
解 正方体、长方体、棱柱、圆柱、圆锥、棱锥、球.(1)注意圆柱与棱柱的区别:圆柱的底面是圆,棱柱的底面是多边形,圆柱的侧面是曲面,棱柱的侧面是平行四边形.(2)棱柱与棱锥的区别:棱锥的底面是多边形,圆锥的底面是圆,棱锥的侧面是三角形,圆锥的侧面是曲面.说出下列立体图形(如图4 - 2所示)的名称.图4 - 22.观察小明的房间,说说你能看到哪些立体图形?练习球、圆柱、长方体、正方体、棱柱、圆锥.3.平面图形 说一说下面这些几何图形又有什么共同特点? 这些几何图形的各部分都在同一平面内,它们是平面图形. 观察与思考 下面各图中包含哪些简单的平面图形?请再举出一些平面图形的例子.典例精析解析:选项A中,球、圆锥是立体图形,故A错误;选项B中,棱锥、棱柱是立体图形,故B错误;选项D中,长方体是立体图形,故D错误.图形的各部分都在同一平面内的图形叫做平面图形.熟练掌握平面图形与立体图形的区别是解题的关键.下列各组图形中都是平面图形的是 ( )
A.三角形、圆、球、圆锥 B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆 D.点、角、线段、长方体C如图所示的是一座房子的平面图,组成这幅图的几何图形有 .?练习三角形、正方形、长方形、梯形.4. 几何图形的构成元素问题: 这些几何体是由什么围成的吗?它们有什么不同吗?合作探究它们都有表面,包围着体的是面.曲面曲面平面平面观察下列图形,你看到了哪些面?面有平的面和曲的面两种下列几何体的面哪些是平的?哪些是曲的?立方体长方体圆柱体圆锥体球体3.几何图形都是由点、线、面、体组成的.1.面与面相交形成线;2.线与线相交得到点;观察发现这可以说成:点动成线. 笔尖可以看作是一个点,这个点在纸上运动时,形成了什么?问题:深入探究你能举出其他“点动成线”的实例吗?线动成面实际生活中的“线动成面”面动成体5.从不同方向看物体及立体图形的展开与折叠合作探究从不同的方向看下面的立体图形,你会得到什么?从正面看从左面看从上面看圆柱体从正面看从左面看从上面看圆锥从正面看从左面看从上面看四棱锥从正面看从左面看从上面看三棱柱 将一个正方体的表面沿某些棱剪开,能展开成什么样的图形?圆柱体、圆锥体展开呢?想一想圆柱圆锥说一说:下面图形是一些立体图形的表面展开图,你能说出这些立体图形的名字吗?典例精析(2018·河南中考)某正方体的每个面上都有一个汉字,如图所示的是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是 ( )
A.厉 B.害 C.了 D.我D解析:正方体的表面展开图中,相对的面之间一定相隔一个正方形,根据这一特点作答.“我”与“国”相对;“厉”与“了”相对;“害”与“的”相对.(2018·陕西中考)如图所示的是一个几何体的表面展开图,则该几何体是 ( )
?
A.正方体 B.长方体
C.三棱柱 D.四棱锥练习C1.下列图形不是立体图形的是 ( )
A.球 B.圆柱 C.圆锥 D.圆D2.(2019·山东潍坊期末)如图4 - 16所示,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,则这个平面图形是图4 - 17中的 ( )图4 - 17B3.如图4 - 18所示的是一个立方体纸盒的展开图,使展开图折叠成正方体后相对面上的两个数互为相反数,则a= ;b= ;c= .?图4 - 18-2-714.分别画出如图4 - 19所示的圆柱、圆锥及球从正面、左面、上面看到的图形.
图4 - 19从正面看从左边看从上面看5.如图4 - 21所示的都是平面图形.图4 - 21(1)每个图形各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入表格中.(2)根据(1)中的结论,推断出一个平面图形的顶点数、边数、区域数之间的关系.812569410156由(1)中的结论得:边数-顶点数+1=区域数.几何图形 立体图形的展开与折叠
同课章节目录
