湘教版七年级数学上册4.2 第2课时 线段的长短比较课件(30张ppt)
文档属性
| 名称 | 湘教版七年级数学上册4.2 第2课时 线段的长短比较课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1011.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-09 23:28:48 | ||
图片预览







文档简介
课件30张PPT。新课标 第4章图形的认识4.2 线段、射线、直线第2课时 线段的长短比较学习目标1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短. (重点)
2. 理解线段等分点的意义.
3. 能够运用线段的和、差、倍、分关系求线段的长度. (重点、难点)
4. 体会文字语言、符号语言和图形语言的相互转化.
5. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用. (难点)素养提升1.会比较线段的长度,理解线段的和、差、倍、分的意义,会用直尺和圆规作一条线段等于已知线段.
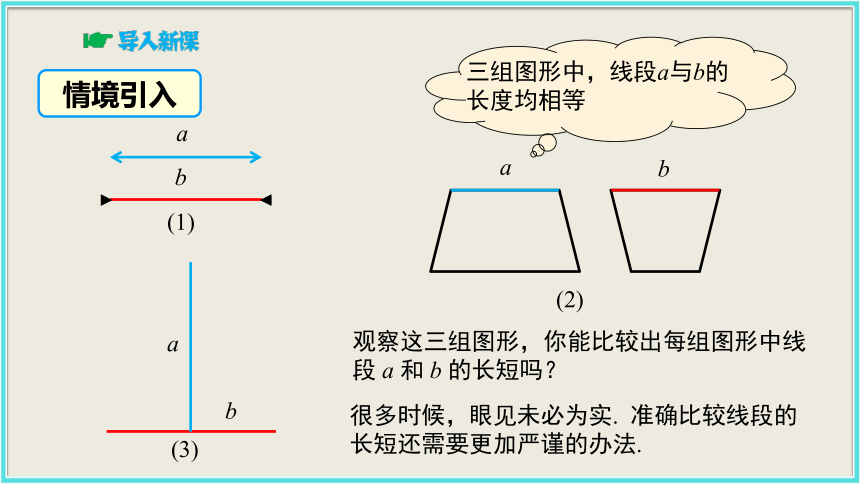
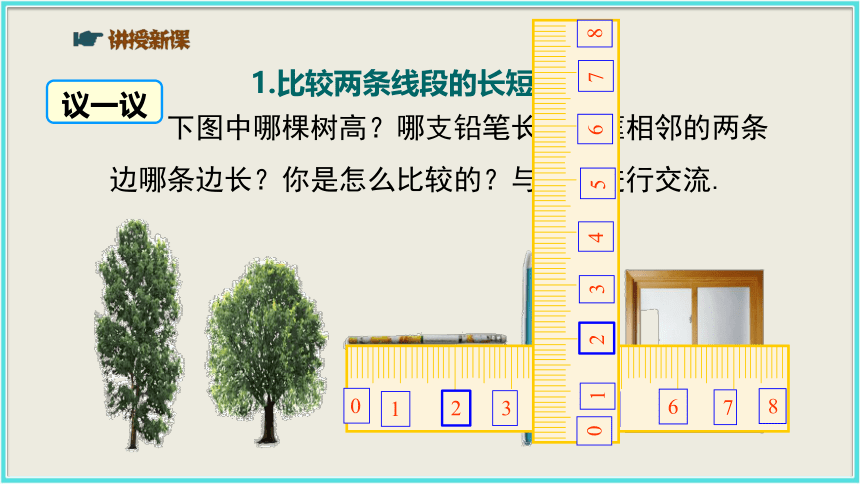
2.理解线段中点的意义,会进行线段长度的计算.情境引入观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.(1)(2)(3)abaabb1.比较两条线段的长短议一议 下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?与同伴进行交流.思考:怎样比较两条线段的长短??(1) 度量法(2) 叠合法 将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上. 用刻度尺量出它们的长度,再进行比较.叠合法结论:1. 若点 A 与点 C 重合,点 B 落
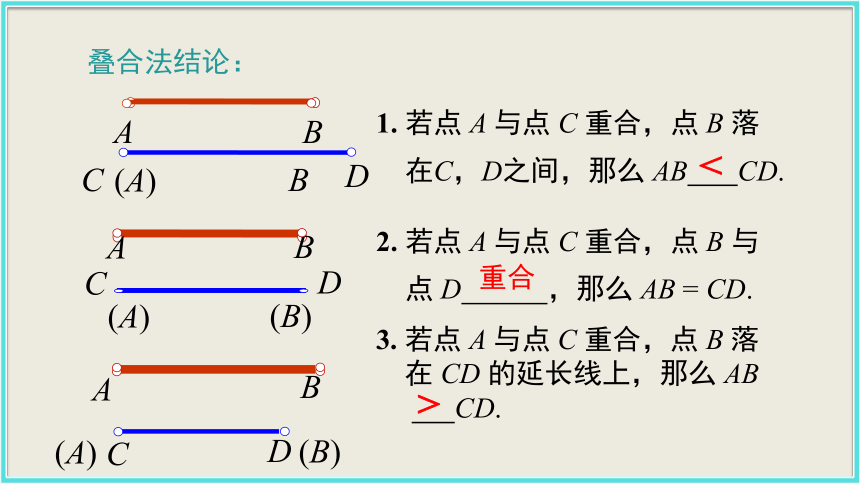
在C,D之间,那么 AB CD.<2. 若点 A 与点 C 重合,点 B 与
点 D ,那么 AB = CD.3. 若点 A 与点 C 重合,点 B 落
在 CD 的延长线上,那么 AB
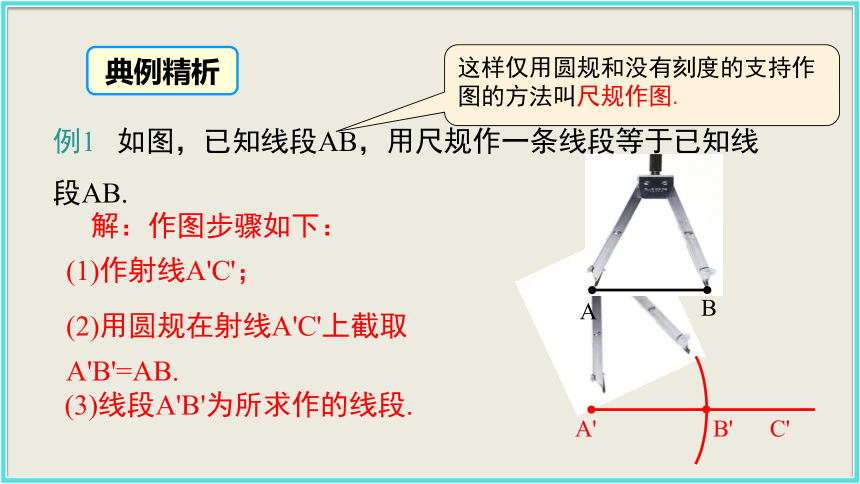
CD.重合>例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB.(1)作射线A'C';(2)用圆规在射线A'C'上截取A'B'=AB.(3)线段A'B'为所求作的线段.A' C'B'解:作图步骤如下:典例精析这样仅用圆规和没有刻度的支持作图的方法叫尺规作图.如下图所示的是一张三角形的纸片,你能准确地比较线段AB与线段BC的长度吗?典例精析解析:可用“重叠法”或“度量法”比较.
解法1 重叠法:把边BC折到AB上,可知点C在线段AB上,所以AB>BC.
解法2 度量法:用直尺测出AB=2 cm,BC=1.5 cm,
所以AB>BC.用圆规比较图中的四条线段的长度,其中最长的是( )
A.BC B.AB
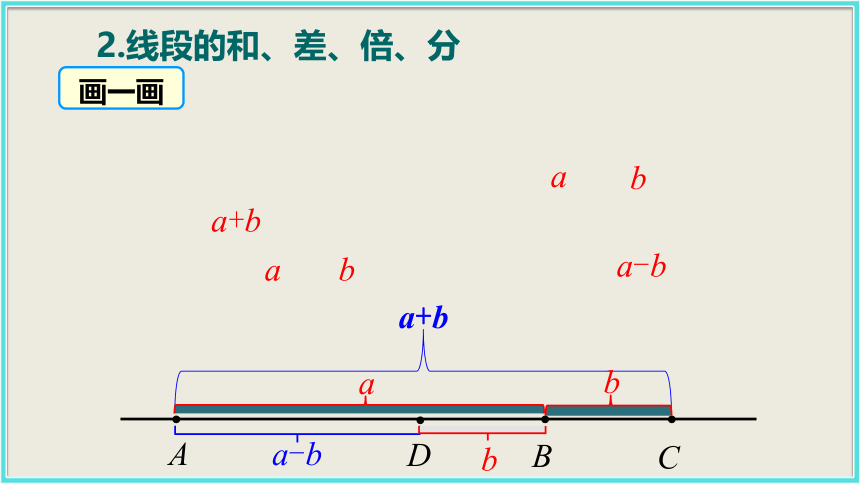
C.DA D.CD练习A2.线段的和、差、倍、分 在直线上画出线段 AB=a?,再在 AB 的延长线上画线段 BC=b,线段 AC 就是 与 的和,记作 AC= . 如果在 AB 上画线段 BD=b,那么线段 AD 就是 与 的差,记作AD= . ABCa+ba-b画一画aba+baba-b 在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?ABMABM 如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点. 类似地,还有线段的三等分点、四等分点等.线段的三等分点线段的四等分点M 是线段 AB 的中点几何语言:因为M 是线段 AB 的中点
所以 AM = MB = AB
( 或 AB = 2 AM = 2 MB )反之也成立:因为 AM = MB = AB
( 或 AB = 2 AM = 2 AB )
所以 M 是线段 AB 的中点知识要点点 M , N 是线段 AB 的三等分点:AM = MN = NB = ___ AB(或 AB = ___AM = ___ MN = ___NB)例2 如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度. 解:因为AB=4 cm,BC=3 cm,
所以AC=AB+ BC=7 cm. 因为点O是线段AC的中点,
所以OC= AC=3.5 cm.所以OB=OC-BC=3.5-3=0.5(cm). (1)逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.计算线段长度的一般方法: (2)整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.归纳总结如下图所示,已知线段a,b,借助直尺和圆规作一条线段,使它等于a+b.典例精析解 ①作射线AD;
②在AD上顺次截取AB=a,BC=b,则AC就是所要求作的线段(如下图所示).
用尺规作线段的和,一般都在所作射线上依次截取;作线段的差,要在长的线段内依次截取,余下的线段即为所求.已知线段a,b,求作一条线段,使它等于2a-b.练习3.两点之间线段最短合作探究??AB 如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.发现:两点之间的所有连线中,线段最短 2.我们把两点之间线段的长度,叫做这两点之间的距离.1.上述发现可以总结为:两点之间,线段最短知识要点典例精析 [解析] 在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.例4 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?解:连接AB,交MN于点P,则这个货站应建在点P处. (1)两点之间的距离的概念描述的是数量,而不是图形,指的是连接两点的线段的长度,而不是线段本身.
(2)在解决选择位置、求最短距离等问题时,通常转化为“两点之间线段最短”.归纳总结1.用圆规截取的方法比较图中下列两组线段的大小:(1) AC 和AB; (2) BC 和AB.(1) AC < AB(2) BC < AB2.如图,AB+BC AC,AC+BC AB,
AB+AC BC(填“>”“<”或“=”).
其中蕴含的数学道理是 .>>>两点之间线段最短3.已知线段 AB = 6 cm,延长 AB 到 C,使 BC = 2 AB,若 D 为 AB 的中点,则线段 DC 的长为________.15 cm4.点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若BC=5,则AC=_________.11或15.如图,已知线段a,b(a>b)作一条线段使它等于a-b. 解:作图步骤如下:Ab (1) 作射线AF;F (2) 在射线AF上截取AC=a;aCB (3) 在线段AC截取AB=b. 则线段BC就是所要求作的线段.6.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.AD=10x=20 .解:设AB=2x,BC=5x,CD=3x,所以AD=AB+BC+CD=10x.因为M是AD的中点,所以AM=MD=5x,所以BM=AM-AB=3x.因为BM=6,即3x=6,所以x=2. 故CM=MD-CD=2x=4,线段的长短比较
2. 理解线段等分点的意义.
3. 能够运用线段的和、差、倍、分关系求线段的长度. (重点、难点)
4. 体会文字语言、符号语言和图形语言的相互转化.
5. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用. (难点)素养提升1.会比较线段的长度,理解线段的和、差、倍、分的意义,会用直尺和圆规作一条线段等于已知线段.
2.理解线段中点的意义,会进行线段长度的计算.情境引入观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.(1)(2)(3)abaabb1.比较两条线段的长短议一议 下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?与同伴进行交流.思考:怎样比较两条线段的长短??(1) 度量法(2) 叠合法 将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上. 用刻度尺量出它们的长度,再进行比较.叠合法结论:1. 若点 A 与点 C 重合,点 B 落
在C,D之间,那么 AB CD.<2. 若点 A 与点 C 重合,点 B 与
点 D ,那么 AB = CD.3. 若点 A 与点 C 重合,点 B 落
在 CD 的延长线上,那么 AB
CD.重合>例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB.(1)作射线A'C';(2)用圆规在射线A'C'上截取A'B'=AB.(3)线段A'B'为所求作的线段.A' C'B'解:作图步骤如下:典例精析这样仅用圆规和没有刻度的支持作图的方法叫尺规作图.如下图所示的是一张三角形的纸片,你能准确地比较线段AB与线段BC的长度吗?典例精析解析:可用“重叠法”或“度量法”比较.
解法1 重叠法:把边BC折到AB上,可知点C在线段AB上,所以AB>BC.
解法2 度量法:用直尺测出AB=2 cm,BC=1.5 cm,
所以AB>BC.用圆规比较图中的四条线段的长度,其中最长的是( )
A.BC B.AB
C.DA D.CD练习A2.线段的和、差、倍、分 在直线上画出线段 AB=a?,再在 AB 的延长线上画线段 BC=b,线段 AC 就是 与 的和,记作 AC= . 如果在 AB 上画线段 BD=b,那么线段 AD 就是 与 的差,记作AD= . ABCa+ba-b画一画aba+baba-b 在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?ABMABM 如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点. 类似地,还有线段的三等分点、四等分点等.线段的三等分点线段的四等分点M 是线段 AB 的中点几何语言:因为M 是线段 AB 的中点
所以 AM = MB = AB
( 或 AB = 2 AM = 2 MB )反之也成立:因为 AM = MB = AB
( 或 AB = 2 AM = 2 AB )
所以 M 是线段 AB 的中点知识要点点 M , N 是线段 AB 的三等分点:AM = MN = NB = ___ AB(或 AB = ___AM = ___ MN = ___NB)例2 如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度. 解:因为AB=4 cm,BC=3 cm,
所以AC=AB+ BC=7 cm. 因为点O是线段AC的中点,
所以OC= AC=3.5 cm.所以OB=OC-BC=3.5-3=0.5(cm). (1)逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.计算线段长度的一般方法: (2)整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.归纳总结如下图所示,已知线段a,b,借助直尺和圆规作一条线段,使它等于a+b.典例精析解 ①作射线AD;
②在AD上顺次截取AB=a,BC=b,则AC就是所要求作的线段(如下图所示).
用尺规作线段的和,一般都在所作射线上依次截取;作线段的差,要在长的线段内依次截取,余下的线段即为所求.已知线段a,b,求作一条线段,使它等于2a-b.练习3.两点之间线段最短合作探究??AB 如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.发现:两点之间的所有连线中,线段最短 2.我们把两点之间线段的长度,叫做这两点之间的距离.1.上述发现可以总结为:两点之间,线段最短知识要点典例精析 [解析] 在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.例4 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?解:连接AB,交MN于点P,则这个货站应建在点P处. (1)两点之间的距离的概念描述的是数量,而不是图形,指的是连接两点的线段的长度,而不是线段本身.
(2)在解决选择位置、求最短距离等问题时,通常转化为“两点之间线段最短”.归纳总结1.用圆规截取的方法比较图中下列两组线段的大小:(1) AC 和AB; (2) BC 和AB.(1) AC < AB(2) BC < AB2.如图,AB+BC AC,AC+BC AB,
AB+AC BC(填“>”“<”或“=”).
其中蕴含的数学道理是 .>>>两点之间线段最短3.已知线段 AB = 6 cm,延长 AB 到 C,使 BC = 2 AB,若 D 为 AB 的中点,则线段 DC 的长为________.15 cm4.点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若BC=5,则AC=_________.11或15.如图,已知线段a,b(a>b)作一条线段使它等于a-b. 解:作图步骤如下:Ab (1) 作射线AF;F (2) 在射线AF上截取AC=a;aCB (3) 在线段AC截取AB=b. 则线段BC就是所要求作的线段.6.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.AD=10x=20 .解:设AB=2x,BC=5x,CD=3x,所以AD=AB+BC+CD=10x.因为M是AD的中点,所以AM=MD=5x,所以BM=AM-AB=3x.因为BM=6,即3x=6,所以x=2. 故CM=MD-CD=2x=4,线段的长短比较
同课章节目录
