湘教版七年级数学上册:4.3.2 第2课时 余角和补角-课件25张PPT
文档属性
| 名称 | 湘教版七年级数学上册:4.3.2 第2课时 余角和补角-课件25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 803.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-09 00:00:00 | ||
图片预览






文档简介
课件25张PPT。新课标 第4章图形的认识4.3.2 第2课时 余角和补角学习目标1. 了解余角、补角的概念,掌握余角和补角的性质.(重点)
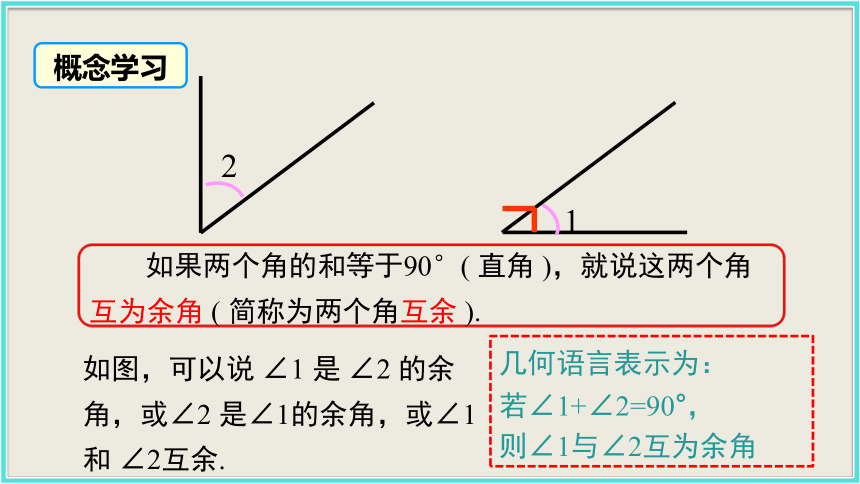
2. 能利用余角、补角的知识解决相关问题.(难点)素养提升理解两角互余、互补的概念和性质,会求一个角的余角或补角,提升运算能力.12比萨斜塔 13比萨斜塔 活动:将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.思考:1. ∠1 与∠2 有什么数量关系?∠1+∠2 = 90°2. ∠3与∠4有什么数量关系?∠3+∠4 = 180°1.余角和补角的概念 如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).如图,可以说 ∠1 是 ∠2 的余角,或∠2 是∠1的余角,或∠1和 ∠2互余.概念学习几何语言表示为:
若∠1+∠2=90°,
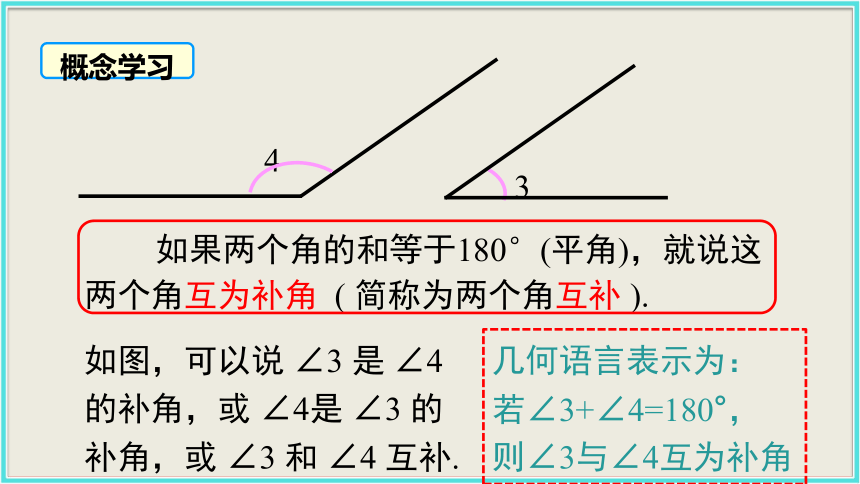
则∠1与∠2互为余角 如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).如图,可以说 ∠3 是 ∠4 的补角,或 ∠4是 ∠3 的补角,或 ∠3 和 ∠4 互补.概念学习几何语言表示为:
若∠3+∠4=180°,
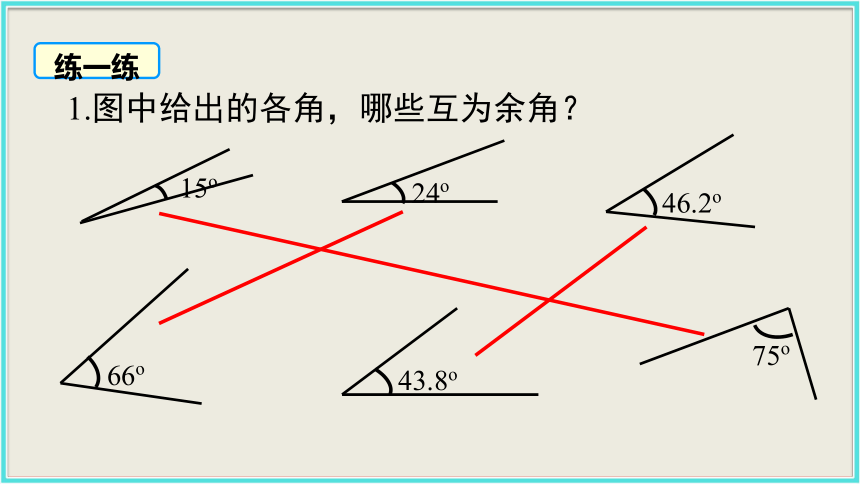
则∠3与∠4互为补角1.图中给出的各角,哪些互为余角?15o24o66o75o46.2o43.8o练一练2.图中给出的各角,哪些互为补角?练一练27°37′117°37′85°175°58°148°45°135°103°13°观察与思考(90-x)°(180-x)°观察可得结论:
锐角的补角比它的余角大_____.90°
5)如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角互为余角. ( )3)同一个角的补角比它的余角大多少90度. ( )4)互余的两个角一定都是锐角,两个锐角一定互余. ( ) 2)一个角的补角必为钝角. ( ) 1)一个角的余角必为锐角. ( )×√×√×判一判例1 若一个角为35°35'35″,写出它的余角和补角.解析 在计算过程中,将90°写为89°59'60″,再与35°35'35″相减较为方便.将180°写为179°59'60″,再与35°35'35″相减较为方便,也可以将35°35'35″的余角加上90°就是35°35'35″的补角.∠α的余角=90 °-∠α,∠α的补角=180 °-∠α,∠α的补角=∠α的余角+90 °.解 35°35'35″的余角为:
90°-35°35'35″=89°59'60″-35°35'35″=54°24'25″,
35°35'35″的补角为:
180°-35°35'35″=179°59'60″-35°35'35″=144°24'25″.3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,求∠C的度数.解:因为∠A与∠B互余,∠A=60°,所以∠B=90°-60°=30°,又∠B与∠C互补,所以∠C=180°-30°=150°.练习∠1 与∠2,∠3都互为补角,
∠2 与∠3 的大小有什么关系? 思考:同角 (等角) 的补角相等.结论:∠2=180°-∠1∠3=180°-∠1同角 (等角) 的余角相等.类似地,可以得到:=2.余角和补角的性质 如图,已知∠AOB=90°, ∠AOC= ∠BOD,则与∠AOC互余的角有__________________.∠BOC 和 ∠AOD练一练例3 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角? 解:因为点A,O,B在同一直线
上,所以 ∠AOC 和 ∠BOC 互为补角.又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,所以∠COD+∠COE= ∠AOC+
∠BOC = (∠AOC+∠BOC ) = 90°.所以∠COD和∠COE互为余角,同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.变式训练:如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是_______________,∠COD的余角是_________________;
(2 )OE是∠BOC的平分线吗?请说明理由.∠COE、∠BOE∠COE、∠BOE解:OE平分∠BOC,理由如下:∵∠DOE=90°,∴∠AOD+∠BOE=90°,
∴∠COD+∠DOE=90°,
∴∠AOD+∠BOE=∠COD+∠DOE,
∵OD平分∠AOC∴∠AOD=∠COD,
∴∠COE=∠BOE,∴OE平分∠BOC.例4 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.解:设∠AOB=x,
因为∠AOC与∠AOB互补,
则∠AOC=180°-x.
因为OM,ON分别为∠AOC,
∠AOB的平分线,所以∠AOM= ,∠AOM= .所以解得x=50°,则180°-x=130°.即∠AOB=50°,∠AOC=130°.1. (2018·德州中考)如图4 - 71所示,将一副三角尺按不同的位置摆放,下列摆放方式中,∠a与∠β互余的是 ( )A.图① B.图② C.图③ D.图④A2.如果∠1和∠2互补,∠1和∠3互补,那么∠2和∠3的关系是 ( )
A.相等 B.互补
C.互余 D.不能确定
3.若一个角的3倍比这个角的补角的2倍还少5°,则这个角等于 .
4.如果∠α和∠β互补,且∠α>∠β,那么下列表示角的式子中:①90°-∠β;②∠α-90°;③ (∠α+∠β);④ (∠α-∠β).能表示∠β的余角的是 (填序号).?
?A71°① ② ④5.如图所示,已知∠AOB=155°,∠AOC=∠BOD=90°.
(1)写出与∠COD互余的角;
(2)求∠COD的度数;
(3)图中是否有互补的角?若有,请写出来.解:(1)因为∠AOC=∠BOD=90°,所以∠COD+∠AOD=90°,∠COD+∠BOC=90°,所以与∠COD互余的角是∠AOD和∠BOC.
(2)∠BOC=∠AOB-∠AOC=65°,所以∠COD=∠BOD-∠BOC=25°.
(3)有.∠COD与∠AOB互补,∠AOC与∠BOD互补.同角或等角的
补角相等同角或等角的
余角相等
2. 能利用余角、补角的知识解决相关问题.(难点)素养提升理解两角互余、互补的概念和性质,会求一个角的余角或补角,提升运算能力.12比萨斜塔 13比萨斜塔 活动:将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.思考:1. ∠1 与∠2 有什么数量关系?∠1+∠2 = 90°2. ∠3与∠4有什么数量关系?∠3+∠4 = 180°1.余角和补角的概念 如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).如图,可以说 ∠1 是 ∠2 的余角,或∠2 是∠1的余角,或∠1和 ∠2互余.概念学习几何语言表示为:
若∠1+∠2=90°,
则∠1与∠2互为余角 如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).如图,可以说 ∠3 是 ∠4 的补角,或 ∠4是 ∠3 的补角,或 ∠3 和 ∠4 互补.概念学习几何语言表示为:
若∠3+∠4=180°,
则∠3与∠4互为补角1.图中给出的各角,哪些互为余角?15o24o66o75o46.2o43.8o练一练2.图中给出的各角,哪些互为补角?练一练27°37′117°37′85°175°58°148°45°135°103°13°观察与思考(90-x)°(180-x)°观察可得结论:
锐角的补角比它的余角大_____.90°
5)如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角互为余角. ( )3)同一个角的补角比它的余角大多少90度. ( )4)互余的两个角一定都是锐角,两个锐角一定互余. ( ) 2)一个角的补角必为钝角. ( ) 1)一个角的余角必为锐角. ( )×√×√×判一判例1 若一个角为35°35'35″,写出它的余角和补角.解析 在计算过程中,将90°写为89°59'60″,再与35°35'35″相减较为方便.将180°写为179°59'60″,再与35°35'35″相减较为方便,也可以将35°35'35″的余角加上90°就是35°35'35″的补角.∠α的余角=90 °-∠α,∠α的补角=180 °-∠α,∠α的补角=∠α的余角+90 °.解 35°35'35″的余角为:
90°-35°35'35″=89°59'60″-35°35'35″=54°24'25″,
35°35'35″的补角为:
180°-35°35'35″=179°59'60″-35°35'35″=144°24'25″.3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,求∠C的度数.解:因为∠A与∠B互余,∠A=60°,所以∠B=90°-60°=30°,又∠B与∠C互补,所以∠C=180°-30°=150°.练习∠1 与∠2,∠3都互为补角,
∠2 与∠3 的大小有什么关系? 思考:同角 (等角) 的补角相等.结论:∠2=180°-∠1∠3=180°-∠1同角 (等角) 的余角相等.类似地,可以得到:=2.余角和补角的性质 如图,已知∠AOB=90°, ∠AOC= ∠BOD,则与∠AOC互余的角有__________________.∠BOC 和 ∠AOD练一练例3 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角? 解:因为点A,O,B在同一直线
上,所以 ∠AOC 和 ∠BOC 互为补角.又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,所以∠COD+∠COE= ∠AOC+
∠BOC = (∠AOC+∠BOC ) = 90°.所以∠COD和∠COE互为余角,同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.变式训练:如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是_______________,∠COD的余角是_________________;
(2 )OE是∠BOC的平分线吗?请说明理由.∠COE、∠BOE∠COE、∠BOE解:OE平分∠BOC,理由如下:∵∠DOE=90°,∴∠AOD+∠BOE=90°,
∴∠COD+∠DOE=90°,
∴∠AOD+∠BOE=∠COD+∠DOE,
∵OD平分∠AOC∴∠AOD=∠COD,
∴∠COE=∠BOE,∴OE平分∠BOC.例4 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.解:设∠AOB=x,
因为∠AOC与∠AOB互补,
则∠AOC=180°-x.
因为OM,ON分别为∠AOC,
∠AOB的平分线,所以∠AOM= ,∠AOM= .所以解得x=50°,则180°-x=130°.即∠AOB=50°,∠AOC=130°.1. (2018·德州中考)如图4 - 71所示,将一副三角尺按不同的位置摆放,下列摆放方式中,∠a与∠β互余的是 ( )A.图① B.图② C.图③ D.图④A2.如果∠1和∠2互补,∠1和∠3互补,那么∠2和∠3的关系是 ( )
A.相等 B.互补
C.互余 D.不能确定
3.若一个角的3倍比这个角的补角的2倍还少5°,则这个角等于 .
4.如果∠α和∠β互补,且∠α>∠β,那么下列表示角的式子中:①90°-∠β;②∠α-90°;③ (∠α+∠β);④ (∠α-∠β).能表示∠β的余角的是 (填序号).?
?A71°① ② ④5.如图所示,已知∠AOB=155°,∠AOC=∠BOD=90°.
(1)写出与∠COD互余的角;
(2)求∠COD的度数;
(3)图中是否有互补的角?若有,请写出来.解:(1)因为∠AOC=∠BOD=90°,所以∠COD+∠AOD=90°,∠COD+∠BOC=90°,所以与∠COD互余的角是∠AOD和∠BOC.
(2)∠BOC=∠AOB-∠AOC=65°,所以∠COD=∠BOD-∠BOC=25°.
(3)有.∠COD与∠AOB互补,∠AOC与∠BOD互补.同角或等角的
补角相等同角或等角的
余角相等
同课章节目录
