人教版八年级上册12.1全等三角形 课件(19张)
文档属性
| 名称 | 人教版八年级上册12.1全等三角形 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-10 20:04:08 | ||
图片预览




文档简介
(共39张PPT)
单击页面即可演示
重点:
1、了解全等形及全等三角形的概念
2 、学会找全等三角形的对应边和对应角
3、掌握全等三角形的性质
请欣赏图片
(1)
(2)
(3)
思考
每组的两个图形有什么特点?
大小、形状相同,完全重合
把一块三角板按在硬纸上,画下图形,照图形裁下来的硬纸和三角板一样.把裁下来的硬纸和三角板放在一起,你又发现什么呢?
大家可发现,两个图形都能完全重合 .
能够完全重合的两个图形叫做全等形.
能够完全重合的两个三角形叫做全等三角形.
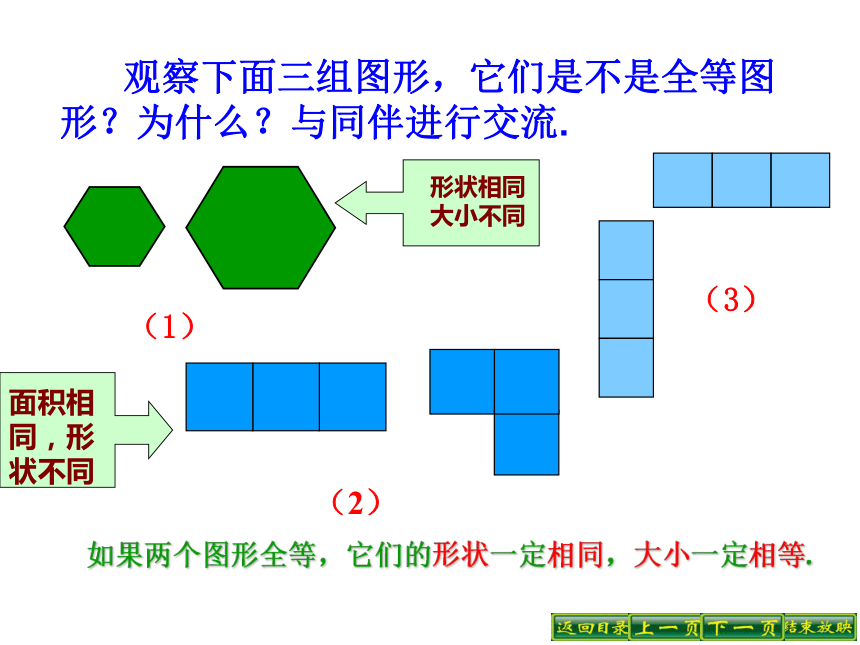
观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流.
(1)
(2)
(3)
如果两个图形全等,它们的形状一定相同,大小一定相等.
平移
1、把?ABC水平平移,得到?DEF
A
B
C
B
C
A
A
E
B
F
C
D
A
翻折
2、把?ABC沿直线BC翻折,得到?DEF
B
C
A
旋转
3、把?ABC沿点A旋转1800,得到?DEF
平移、翻折、旋转后的图形形状大小都没变,与原图形重合
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
三角形中有哪些对应元素
对应顶点(3个)——重合的顶点
对应边(3个)——重合的边
对应角(3个)——重合的角
观察图中的全等三角形
△ ABC ≌△ DEF
注:记全等三角形时,通常把表示对应顶点的字母写在对应的位置上. A与D、B与E、C与F对应。对应顶点要写在对应位置上。
对应顶点:点A和点D,点B和点E,点C和点F,
对应边:AB和DF,AC和DF,BC和EF
对应角:∠A 和∠D, ∠B 和∠E, ∠C 和∠F
1、若△AOC≌△BOD,对应
边是 ,对应角是 ;
A
B
O
C
D
2、若△ABD≌△ACD,对应边是 ,对应角是 ;
A
B
C
D
3、若△ABC≌△DBF,对应
边是 ,对应角是 ;
从以上你能总结出找全等三角形的对应边,对应角的规律吗?
有公共边的,公共边是对应边;
有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角;
一对最长的边是对应边;
一对最短的边是对应边;
一对最大的角是对应角;
一对最小的角是对应角.
在找全等三角形的对应元素时一般有什么规律?
全等三角形的性质:
(全等三角形的对应边相等)
(全等三角形的对应角相等)
全等三角形的对应边相等,对应角相等.
∵△ABC≌ △A′B′C′,
∴AB=A′B′, BC=B′C′,
AC=A′C′,
∴ ∠ A= ∠ A′, ∠ B= ∠B′,
∠ C= ∠C′.
例:如图, 在△ABD ≌ △EBC中,
2.如果AB=3cm,BC=5cm, 求BE、BD的长.
解:∵△ABD ≌ △EBC,
∴AB=EB,BC=BD.
∵AB=3cm,BC=5cm,
∴BE=3cm,BD=5cm.
1.请找出对应边和对应角;
AB EB、BC BD、AD EC;
∠DAB ∠CEB、∠ADB ∠ECB、∠ABD ∠EBC;
与
与
与
与
与
与
3、如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。
如图,已知△ AOC ≌ △BOD
求证:AC∥BD
请同学们说一说,这节课你有哪些收获和体会?
1.你理解了全等三角形的定义了吗?
2、一个图形经过平移、旋转、翻折等变换后的图形与原图形之间有什么关系?
3.你掌握了全等三角形的性质了吗?
4.你学会了找全等三角形的对应边、对应角了吗?
作业:P33 第四题以及长江练习册12.1
单击页面即可演示
重点:
1、了解全等形及全等三角形的概念
2 、学会找全等三角形的对应边和对应角
3、掌握全等三角形的性质
请欣赏图片
(1)
(2)
(3)
思考
每组的两个图形有什么特点?
大小、形状相同,完全重合
把一块三角板按在硬纸上,画下图形,照图形裁下来的硬纸和三角板一样.把裁下来的硬纸和三角板放在一起,你又发现什么呢?
大家可发现,两个图形都能完全重合 .
能够完全重合的两个图形叫做全等形.
能够完全重合的两个三角形叫做全等三角形.
观察下面三组图形,它们是不是全等图形?为什么?与同伴进行交流.
(1)
(2)
(3)
如果两个图形全等,它们的形状一定相同,大小一定相等.
平移
1、把?ABC水平平移,得到?DEF
A
B
C
B
C
A
A
E
B
F
C
D
A
翻折
2、把?ABC沿直线BC翻折,得到?DEF
B
C
A
旋转
3、把?ABC沿点A旋转1800,得到?DEF
平移、翻折、旋转后的图形形状大小都没变,与原图形重合
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
三角形中有哪些对应元素
对应顶点(3个)——重合的顶点
对应边(3个)——重合的边
对应角(3个)——重合的角
观察图中的全等三角形
△ ABC ≌△ DEF
注:记全等三角形时,通常把表示对应顶点的字母写在对应的位置上. A与D、B与E、C与F对应。对应顶点要写在对应位置上。
对应顶点:点A和点D,点B和点E,点C和点F,
对应边:AB和DF,AC和DF,BC和EF
对应角:∠A 和∠D, ∠B 和∠E, ∠C 和∠F
1、若△AOC≌△BOD,对应
边是 ,对应角是 ;
A
B
O
C
D
2、若△ABD≌△ACD,对应边是 ,对应角是 ;
A
B
C
D
3、若△ABC≌△DBF,对应
边是 ,对应角是 ;
从以上你能总结出找全等三角形的对应边,对应角的规律吗?
有公共边的,公共边是对应边;
有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角;
一对最长的边是对应边;
一对最短的边是对应边;
一对最大的角是对应角;
一对最小的角是对应角.
在找全等三角形的对应元素时一般有什么规律?
全等三角形的性质:
(全等三角形的对应边相等)
(全等三角形的对应角相等)
全等三角形的对应边相等,对应角相等.
∵△ABC≌ △A′B′C′,
∴AB=A′B′, BC=B′C′,
AC=A′C′,
∴ ∠ A= ∠ A′, ∠ B= ∠B′,
∠ C= ∠C′.
例:如图, 在△ABD ≌ △EBC中,
2.如果AB=3cm,BC=5cm, 求BE、BD的长.
解:∵△ABD ≌ △EBC,
∴AB=EB,BC=BD.
∵AB=3cm,BC=5cm,
∴BE=3cm,BD=5cm.
1.请找出对应边和对应角;
AB EB、BC BD、AD EC;
∠DAB ∠CEB、∠ADB ∠ECB、∠ABD ∠EBC;
与
与
与
与
与
与
3、如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。
如图,已知△ AOC ≌ △BOD
求证:AC∥BD
请同学们说一说,这节课你有哪些收获和体会?
1.你理解了全等三角形的定义了吗?
2、一个图形经过平移、旋转、翻折等变换后的图形与原图形之间有什么关系?
3.你掌握了全等三角形的性质了吗?
4.你学会了找全等三角形的对应边、对应角了吗?
作业:P33 第四题以及长江练习册12.1
