人教A版高中数学必修一1.3.1 函数的单调性和最大小值 教案
文档属性
| 名称 | 人教A版高中数学必修一1.3.1 函数的单调性和最大小值 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 78.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-12 09:22:36 | ||
图片预览


文档简介
函数单调性与最大(小)值(第一课时)
教材分析:
《函数单调性》是高中数学新教材必修一第二章第三节的内容。在此之前,学生已经学习了函数的概念、定义域、值域、表示法以及在初中学习了一次函数、二次函数、反比例函数等常见函数,也了解了一些函数的增减性,只是当时的研究较为粗略,未明确给出有关函数单调性的定义,对于函数单调性的判断也主要根据图像观察得到,而本小节内容,正是对初中有关内容的一个深化和提高,给出了具体的函数在某个区间上是增函数还是减函数的定义,并明确指出函数的单调性是相对于那个区间的,还介绍了判断函数单调性的两种方法,做到将图像与定义证明结合在一起的思想。
函数的单调性是体现了函数研究的一般方法。这就是加强“数”与“形”的结合,由直观到抽象;由特殊到一般。首先借助对函数图像的观察、分析和归纳,发现函数的增、减变化的直观特征,进一步量化,发现增、减变化数学特征,从而进一步用数学语言刻画。这对研究函数的其他性质,如奇偶性等有借鉴作用。
二、学情分析:
学生已经学习了函数的概念、定义域和值域,因此他们具有了一定的抽象概括、类比归纳,符号表达的能力,在此基础上进一步研究函数的性质,对于他们来说不是太难。但由于函数的图像是发现函数性质的直观载体,因此,在本次教学时,要充分使用信息技术创设教学情境,这样有利于学生更好地观察和探究函数的单调性、最值等性质,同时还要特别注意让学生经历这些概念形成的过程。
三、教学目标:
1、知识与技能:
理解增减函数、单调性、单调区间四个概念:能用自己的语言说出定义,并认识它们是如何得出来的。
掌握函数增减性的证明:掌握判断简单函数的单调区间及证明简单函数在给定区间上的单调性的方法和步骤。
2、过程与方法:
能从具体实例中得出增函数、减函数的定义,培养观察能力和抽象概括能力。
通过知识的获得提高和发展学生自我学习和自我学习和自我发展能力。
3、情感态度与价值观:
借助开放探究的教学方式,张扬学生个性,培养学生科学严谨乐于研究的作风。
四、教学重点:
函数单调性的概念、判断及证明。
五、教学难点:
归纳抽象函数单调性的定义以及根据定义证明函数的单调性。
六、教学方法:
引导发现比较法,借助信息技术辅助法。
七、教学过程:
1、创设情境,引入新课
课前预习:
北京的天气到8月中旬,平均气温、平均降雨量和平均降雨天数等均开始下降,比较适宜举办大型国际体育赛事.
下图是北京市某年8月8日一天24小时内气温随时间变化的曲线图。
教书引导学生识图,捕捉信息,启发学生思考。
问题1:观察图形,你能从图中得到哪些信息?
预案:(1)气温发生了怎样的变化?
(2) 在哪段时间气温升高,在哪段气温降低?
在生活中,有很多数据的变化规律,了解这些数据的变化规律,对我们的生活有很大的帮助。
(设计意图:由生活情境引入新课,激发情趣)
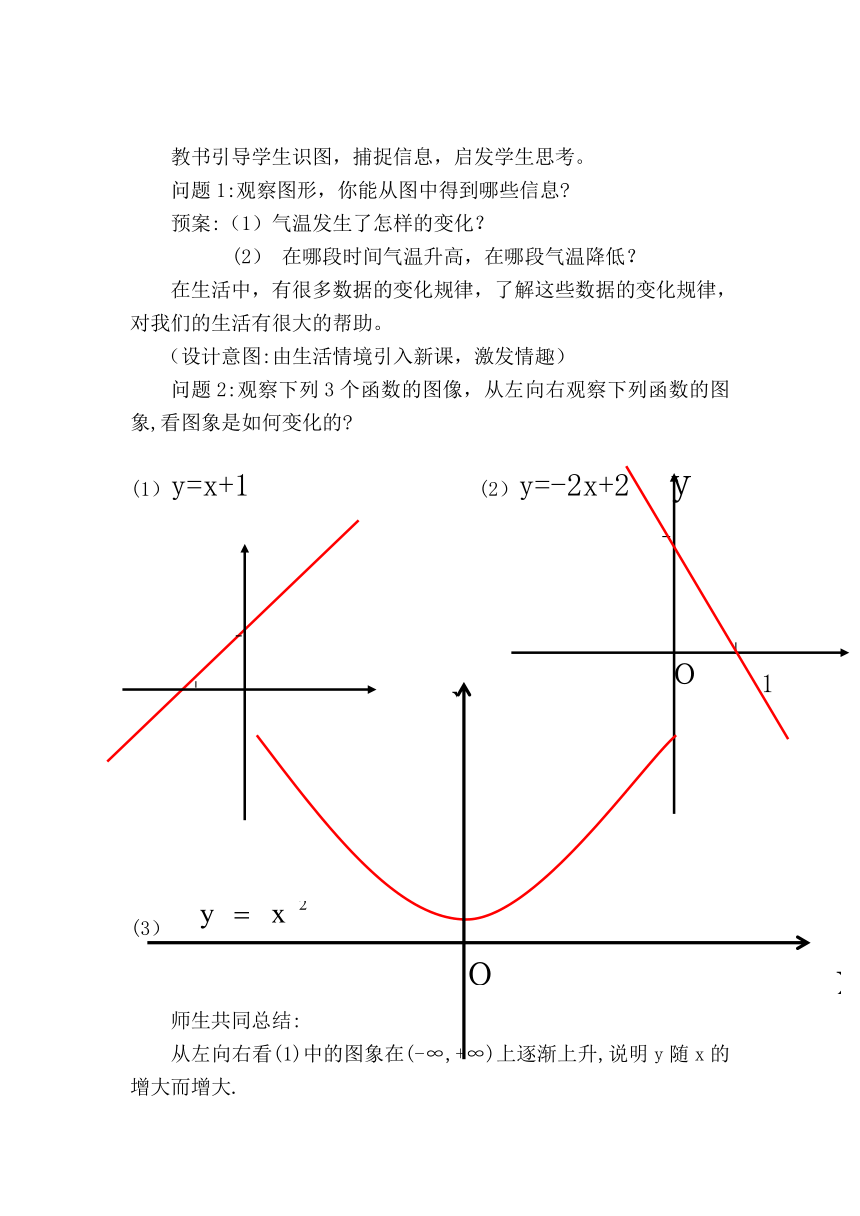
问题2:观察下列3个函数的图像,从左向右观察下列函数的图象,看图象是如何变化的?
(1)y=x+1 (2)y=-2x+2
师生共同总结:
从左向右看(1)中的图象在(-∞,+∞)上逐渐上升,说明y随x的增大而增大.
从左向右看(2)中的图象在(-∞,+∞)上逐渐下降,说明y随x的增大而减小.
从左向右看,(3)中的图象在(-∞,0]上逐渐下降,说明y随x的增大而减小,在[0,+∞)上逐渐上升,说明y随x的增大而增大。
对于函数图像变化问题,很重要的就是描述变化的增与减的问题,我们把函数的这种增
与减的性质称“单调性”。
教师结合上述,写出课题:函数的单调性。
(设计意图:从形到数,借助对函数图像的观察,猜测相应的函数的性质,得出函数单调性的“直观定义”。)
二、抽象思维,形成概念
结合上述直观认识,给出函数德尔单调性的“描述性定义”:
增函数:一般的,设函数的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x1 减函数:如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x1f(x2),那么就说函数f(x)在区间D上是减函数.
单调区间: 如果函数y=f(x)在区间D上是增函数(或减函数),那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调递增(或减)区间.
注意:定义域某个区间D的取值:增、减函数都是对相应的区间
而言的,离开了区间就根本谈不上函数的单调性。
问题3:(1)我们能否说一个函数在x=3时时递增的还是递减的?
答案预设:不能。函数在某一点的函数值是唯一确定的,没有增减变化。
(2)能否脱离区间泛泛而谈某个区间是增函数还是减函数?
答案预设:不能。例:
问题4:由前面的学习.你认为判别单调性的方法有哪些?
答案预设:判别单调性的方法有图像法和定义法
问题5:一次函数的单调性如何?
问题6:二次函数的单调性如何?
(设计意图:从图像直观感知函数的单调性,完成对函数单调性的第一次认识)
3、掌握证法,适当延展。
例1.写出下面函数图像所对应的函数的单调性.
答案预设:函数y= f(x)的单调区间有[-5,2),[-2,1),[1, 3),[3,5]。其中 y= f(x)在区间[-5,2), [1,3)上是减函数,在[-2,1), [3,5]是增函数。
思考1:[-5,-2]是单调减区间,能否说(-5,-2)也是单调减区间?
例2:物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
(师生分析,板书)
练习1:下图是函数的图像,
能说出这个函数分别在哪个区间为增函数和减函数吗?
证明函数在上是增函数.
?(两位同学上黑板做, 全班集体订正)
4. 归纳小结,提高认识
1.函数单调性的定义,注意其关键词:取值、任意、都有。
2.表示单调区间用 和 或 ,连接两个区间。
3.证明函数单调性的步骤: 取值 做差 变形 判断符号 得出结论。
4.研究函数的单调性为以后数形结合思想的应用打下基础。
八、板书设计:
单调性与最大(小)值(第一课时)
通过实例引出课题 函数单调性 例1: 练习1:
1、增函数 解 小结
2、减函数 例2:
3、几何意义 解
九、作业布置:
课本39页习题1.3 A组 1 . 2
思考:课本30页 探究
教材分析:
《函数单调性》是高中数学新教材必修一第二章第三节的内容。在此之前,学生已经学习了函数的概念、定义域、值域、表示法以及在初中学习了一次函数、二次函数、反比例函数等常见函数,也了解了一些函数的增减性,只是当时的研究较为粗略,未明确给出有关函数单调性的定义,对于函数单调性的判断也主要根据图像观察得到,而本小节内容,正是对初中有关内容的一个深化和提高,给出了具体的函数在某个区间上是增函数还是减函数的定义,并明确指出函数的单调性是相对于那个区间的,还介绍了判断函数单调性的两种方法,做到将图像与定义证明结合在一起的思想。
函数的单调性是体现了函数研究的一般方法。这就是加强“数”与“形”的结合,由直观到抽象;由特殊到一般。首先借助对函数图像的观察、分析和归纳,发现函数的增、减变化的直观特征,进一步量化,发现增、减变化数学特征,从而进一步用数学语言刻画。这对研究函数的其他性质,如奇偶性等有借鉴作用。
二、学情分析:
学生已经学习了函数的概念、定义域和值域,因此他们具有了一定的抽象概括、类比归纳,符号表达的能力,在此基础上进一步研究函数的性质,对于他们来说不是太难。但由于函数的图像是发现函数性质的直观载体,因此,在本次教学时,要充分使用信息技术创设教学情境,这样有利于学生更好地观察和探究函数的单调性、最值等性质,同时还要特别注意让学生经历这些概念形成的过程。
三、教学目标:
1、知识与技能:
理解增减函数、单调性、单调区间四个概念:能用自己的语言说出定义,并认识它们是如何得出来的。
掌握函数增减性的证明:掌握判断简单函数的单调区间及证明简单函数在给定区间上的单调性的方法和步骤。
2、过程与方法:
能从具体实例中得出增函数、减函数的定义,培养观察能力和抽象概括能力。
通过知识的获得提高和发展学生自我学习和自我学习和自我发展能力。
3、情感态度与价值观:
借助开放探究的教学方式,张扬学生个性,培养学生科学严谨乐于研究的作风。
四、教学重点:
函数单调性的概念、判断及证明。
五、教学难点:
归纳抽象函数单调性的定义以及根据定义证明函数的单调性。
六、教学方法:
引导发现比较法,借助信息技术辅助法。
七、教学过程:
1、创设情境,引入新课
课前预习:
北京的天气到8月中旬,平均气温、平均降雨量和平均降雨天数等均开始下降,比较适宜举办大型国际体育赛事.
下图是北京市某年8月8日一天24小时内气温随时间变化的曲线图。
教书引导学生识图,捕捉信息,启发学生思考。
问题1:观察图形,你能从图中得到哪些信息?
预案:(1)气温发生了怎样的变化?
(2) 在哪段时间气温升高,在哪段气温降低?
在生活中,有很多数据的变化规律,了解这些数据的变化规律,对我们的生活有很大的帮助。
(设计意图:由生活情境引入新课,激发情趣)
问题2:观察下列3个函数的图像,从左向右观察下列函数的图象,看图象是如何变化的?
(1)y=x+1 (2)y=-2x+2
师生共同总结:
从左向右看(1)中的图象在(-∞,+∞)上逐渐上升,说明y随x的增大而增大.
从左向右看(2)中的图象在(-∞,+∞)上逐渐下降,说明y随x的增大而减小.
从左向右看,(3)中的图象在(-∞,0]上逐渐下降,说明y随x的增大而减小,在[0,+∞)上逐渐上升,说明y随x的增大而增大。
对于函数图像变化问题,很重要的就是描述变化的增与减的问题,我们把函数的这种增
与减的性质称“单调性”。
教师结合上述,写出课题:函数的单调性。
(设计意图:从形到数,借助对函数图像的观察,猜测相应的函数的性质,得出函数单调性的“直观定义”。)
二、抽象思维,形成概念
结合上述直观认识,给出函数德尔单调性的“描述性定义”:
增函数:一般的,设函数的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x1
单调区间: 如果函数y=f(x)在区间D上是增函数(或减函数),那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调递增(或减)区间.
注意:定义域某个区间D的取值:增、减函数都是对相应的区间
而言的,离开了区间就根本谈不上函数的单调性。
问题3:(1)我们能否说一个函数在x=3时时递增的还是递减的?
答案预设:不能。函数在某一点的函数值是唯一确定的,没有增减变化。
(2)能否脱离区间泛泛而谈某个区间是增函数还是减函数?
答案预设:不能。例:
问题4:由前面的学习.你认为判别单调性的方法有哪些?
答案预设:判别单调性的方法有图像法和定义法
问题5:一次函数的单调性如何?
问题6:二次函数的单调性如何?
(设计意图:从图像直观感知函数的单调性,完成对函数单调性的第一次认识)
3、掌握证法,适当延展。
例1.写出下面函数图像所对应的函数的单调性.
答案预设:函数y= f(x)的单调区间有[-5,2),[-2,1),[1, 3),[3,5]。其中 y= f(x)在区间[-5,2), [1,3)上是减函数,在[-2,1), [3,5]是增函数。
思考1:[-5,-2]是单调减区间,能否说(-5,-2)也是单调减区间?
例2:物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
(师生分析,板书)
练习1:下图是函数的图像,
能说出这个函数分别在哪个区间为增函数和减函数吗?
证明函数在上是增函数.
?(两位同学上黑板做, 全班集体订正)
4. 归纳小结,提高认识
1.函数单调性的定义,注意其关键词:取值、任意、都有。
2.表示单调区间用 和 或 ,连接两个区间。
3.证明函数单调性的步骤: 取值 做差 变形 判断符号 得出结论。
4.研究函数的单调性为以后数形结合思想的应用打下基础。
八、板书设计:
单调性与最大(小)值(第一课时)
通过实例引出课题 函数单调性 例1: 练习1:
1、增函数 解 小结
2、减函数 例2:
3、几何意义 解
九、作业布置:
课本39页习题1.3 A组 1 . 2
思考:课本30页 探究
