沪科版八年级上册数学第十四章全等三角形14.2三角形全等的判定提高练习(6课时含答案)
文档属性
| 名称 | 沪科版八年级上册数学第十四章全等三角形14.2三角形全等的判定提高练习(6课时含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-11 07:08:51 | ||
图片预览

文档简介
14.2《三角形全等的判定》提高练习
第1课时《SAS》
一、选择题
1.如图,在5×5格的正方形网格中,与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点在格点上的三角形)共有( )
/
A.5个 B.6个 C.7个 D.8 个
2.如图所示,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则下列结论正确的是( )
①△APC≌△BPD ②△ADO≌△BCO ③△AOP≌△BOP ④△OCP≌△ODP.
/
A.①②③④ B.①②③ C.②③④ D.①③④
3.如图,在△ABD和△ACE中.AB=AC,AD=AE,如果由“SAS”可以判定△ABD≌△ACE,则需补充条件( )
/
A.∠EAD=∠BAC B.∠B=∠C C.∠D=∠E D.∠EAB=∠CAD
4.如图所示,△ABC与△DCE都是等边三角形,AB≠CD,图中有两个三角形是全等的,可以表示为( )
/
A.△ABE≌△DEB B.△ACE≌△DBE C.△ACE≌△BCD D.△AEC≌△BCD
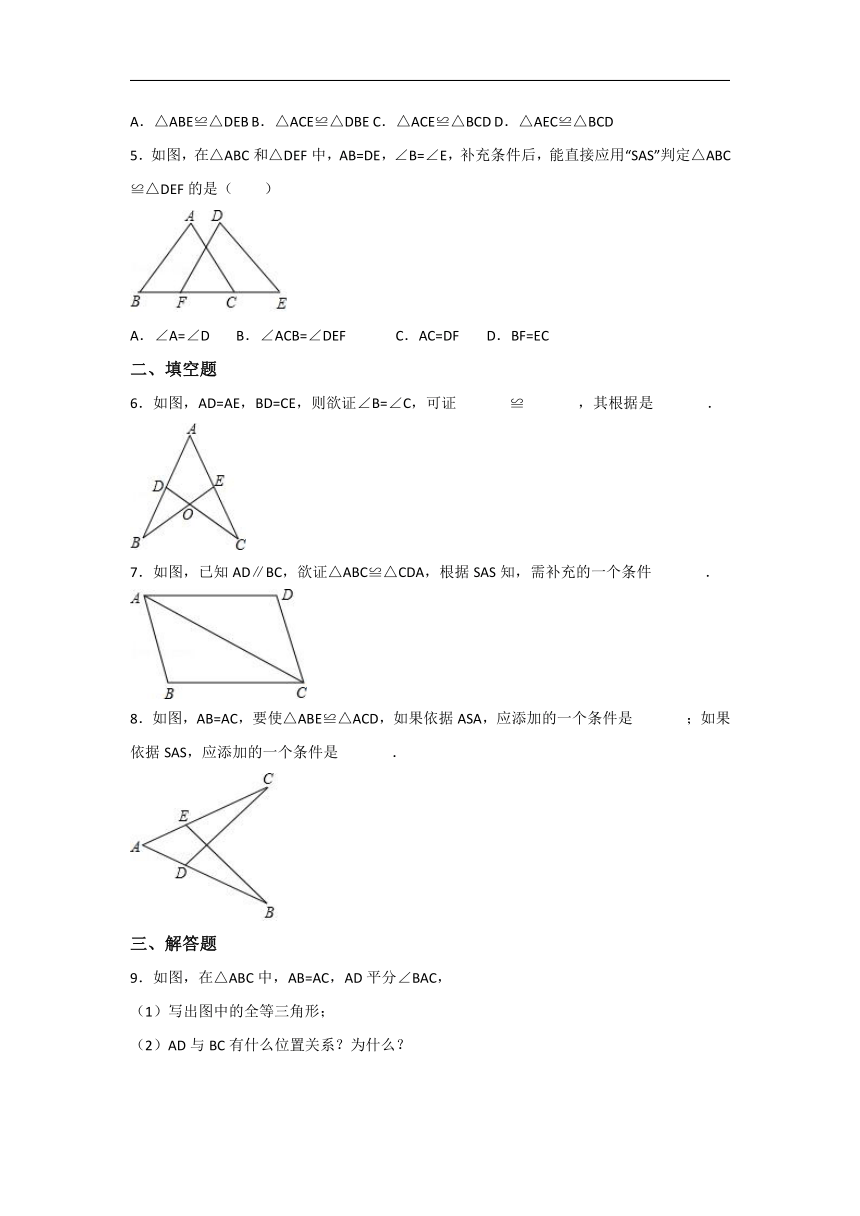
5.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后,能直接应用“SAS”判定△ABC≌△DEF的是( )
/
A.∠A=∠D B.∠ACB=∠DEF C.AC=DF D.BF=EC
二、填空题
6.如图,AD=AE,BD=CE,则欲证∠B=∠C,可证 ≌ ,其根据是 .
/
7.如图,已知AD∥BC,欲证△ABC≌△CDA,根据SAS知,需补充的一个条件 .
/
8.如图,AB=AC,要使△ABE≌△ACD,如果依据ASA,应添加的一个条件是 ;如果依据SAS,应添加的一个条件是 .
/
三、解答题
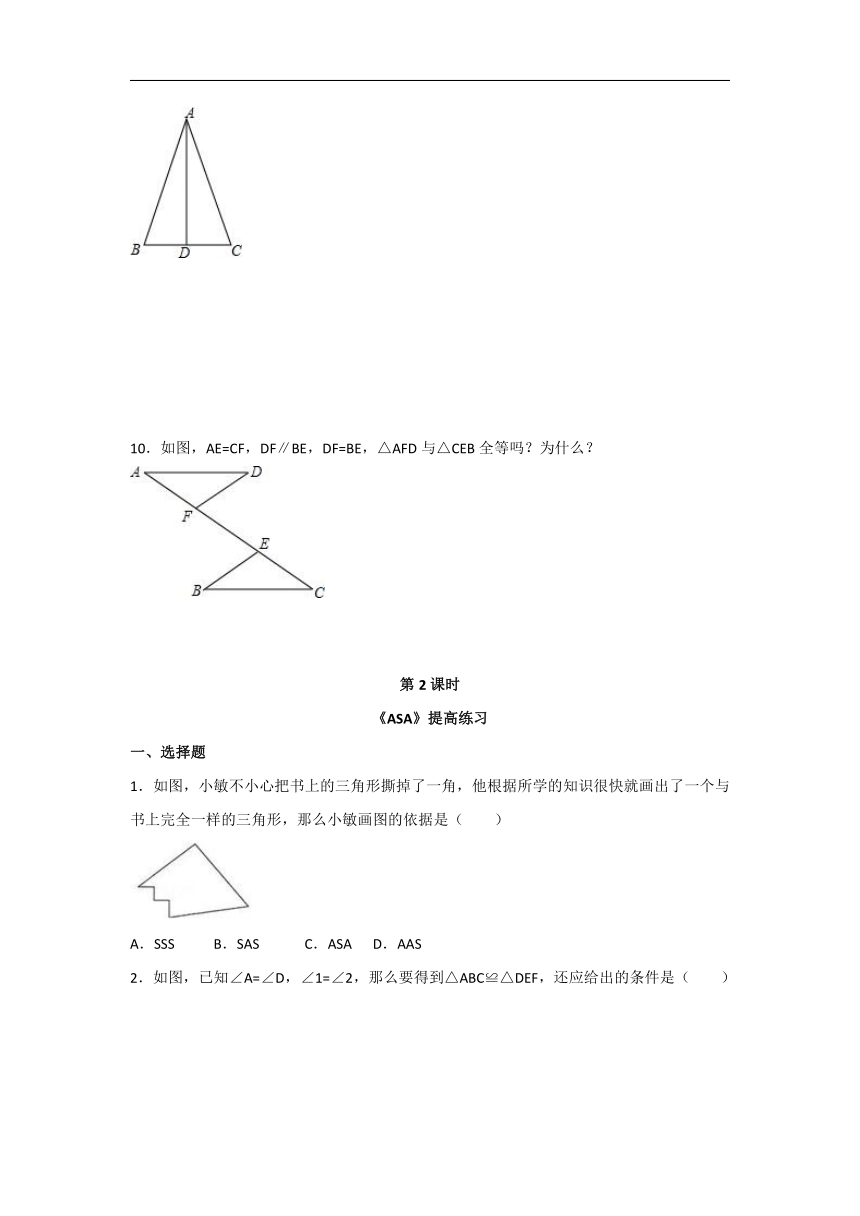
9.如图,在△ABC中,AB=AC,AD平分∠BAC,
(1)写出图中的全等三角形;
(2)AD与BC有什么位置关系?为什么?
/
10.如图,AE=CF,DF∥BE,DF=BE,△AFD与△CEB全等吗?为什么?
/
第2课时
《ASA》提高练习
选择题
1.如图,小敏不小心把书上的三角形撕掉了一角,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小敏画图的依据是( )
/
A.SSS B.SAS C.ASA D.AAS
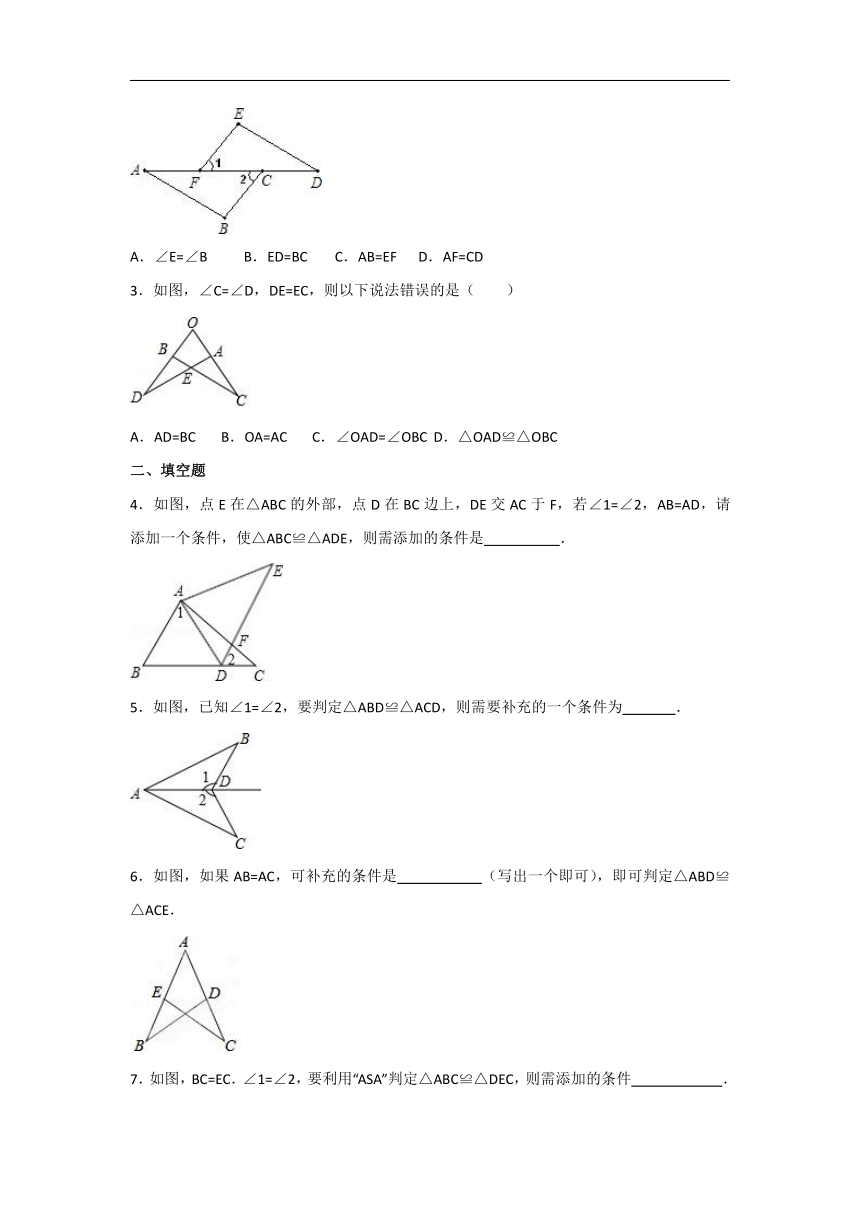
2.如图,已知∠A=∠D,∠1=∠2,那么要得到△ABC≌△DEF,还应给出的条件是( )
/
A.∠E=∠B B.ED=BC C.AB=EF D.AF=CD
3.如图,∠C=∠D,DE=EC,则以下说法错误的是( )
/
A.AD=BC B.OA=AC C.∠OAD=∠OBC D.△OAD≌△OBC
填空题
4.如图,点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2,AB=AD,请添加一个条件,使△ABC≌△ADE,则需添加的条件是 .
/
5.如图,已知∠1=∠2,要判定△ABD≌△ACD,则需要补充的一个条件为 .
/
6.如图,如果AB=AC,可补充的条件是 (写出一个即可),即可判定△ABD≌△ACE.
/
7.如图,BC=EC.∠1=∠2,要利用“ASA”判定△ABC≌△DEC,则需添加的条件 .
/
解答题
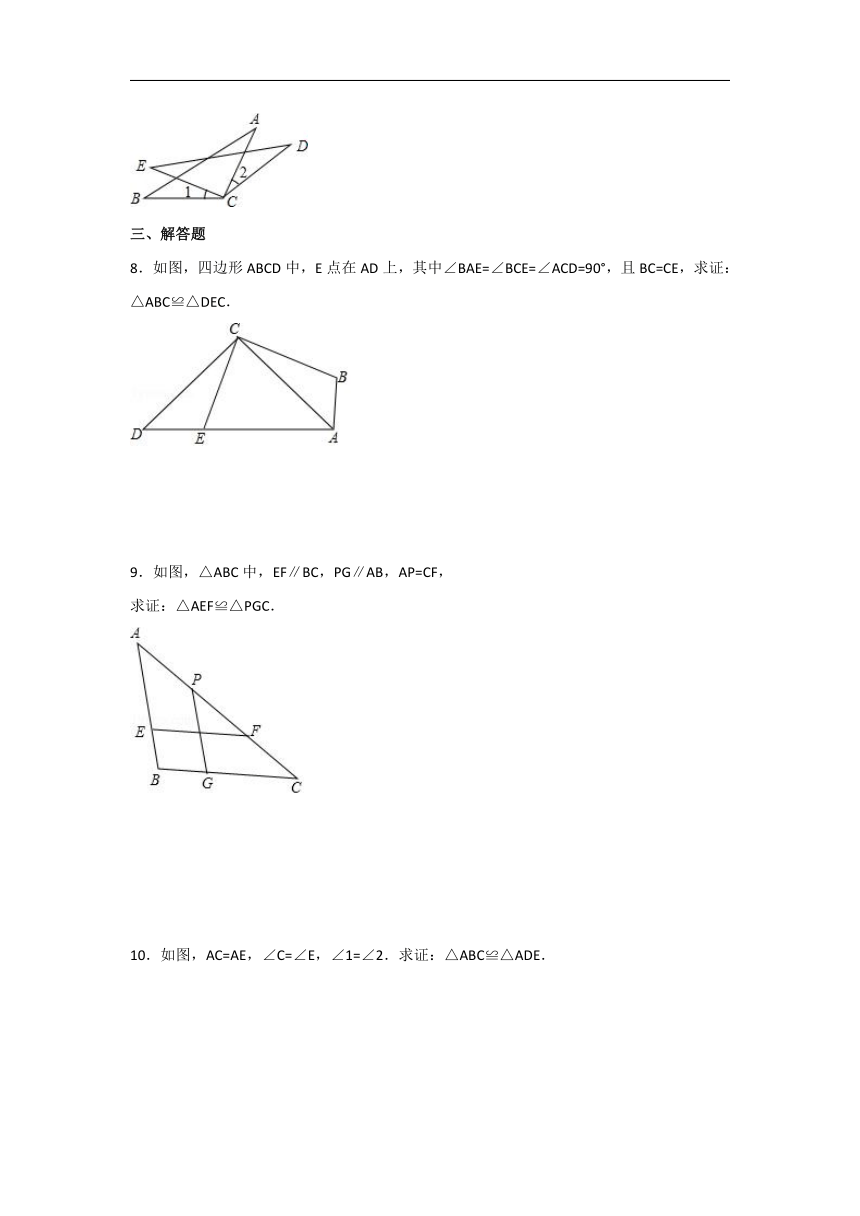
8.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.
/
9.如图,△ABC中,EF∥BC,PG∥AB,AP=CF,
求证:△AEF≌△PGC.
/
10.如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
/
第3课时
《SSS》提高练习
一、选择题
1.如图为作一个角的角平分线的示意图,该作法的依据是全等三角形判定的基本事实,可简写为( )
/
A.SSS B.SAS C.ASA D.AAS
2.如图,AB=AD,BC=CD,点E在AC上,则全等三角形共有( )
/
A.1对 B.2对 C.3对 D.4对
3.如图是5×5的正方形网格,以格点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以作出( )
/
A.2个 B.4个 C.6个 D.8个
4.如图,点E在线段AB上,若AC=AD,CE=DE,则图中的全等三角形共有( )
/
A.1对 B.2对 C.3对 D.4对
二、填空题
5.如图,AB=AC,BE=CD,要使△ABE≌△ACD,依据SSS,则还需添加条件 .
/
6.如图,如果AB=AC,可补充的条件是 (写出一个即可),即可判定△ABD≌△ACE.
/
7.如图,已知AD=BC,根据“SSS”,还需要一个条件 ,可证明△ABC≌△BAD;根据“要SAS”,还需要一个条件 ,可证明△ABC≌△BAD.
/
8、△ABC和△A′B′C′中,若AB=A′B′,BC=B′C′,则需要补充条件 可得到△ABC≌△A′B′C′.
三、解答题
9.如图,在四边形ABCD中,AB=AD,CB=CD.请你添加一条线把它分成两个全等三角形,并给出证明.
/
10.证明:如果两个三角形有两条边和其中一边上的中线分别相等,那么这两个三角形全等.
第4课时
《其他判定两个三角形全等的条件》提高练习
一、选择题
1.如图,下列条件不能证明△ABC≌△DCB的是( )
/
A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D D.AB=DC,∠A=∠D
2.如图,AC⊥BE,∠A=∠E,不能判断△ABC≌△EDC的条件是( )
/
A.BC=DC B.∠B=∠CDE C.AB=DE D.AC=CE
3.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
/
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
4.如图,AC、BD相交于点O,∠A=∠D,要使得△AOB≌△DOC,还需补充一个条件,下面补充的条件不一定正确的是( )
/
A.OA=OD B.AB=DC C.OB=OC D.∠ABO=∠DCO
5.如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△OAB≌△COD,这个条件是( )
/
A.AC=BD B.OD=OC C.∠A=∠C D.OA=OB
二、填空题
6.如图,已知∠BAC=∠DAC,则再添加一个条件 ,可使△ABC≌△ADC.
/
7.如图,在四边形ABCD中,AB=CD,AD=BC,对角线AC、BD交于点O,则图中共有全等三角形 对.
/
8.如图,已知点A、F、C、E在同一直线上,∠1=∠2,AB=DE,请你添加一个条件 (只填一个即可)使△ABC≌△EDF.
/
三、解答题
9.已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,
求证:△ABC≌△DEF.
/
10.已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,
求证:△AOB≌△DOC.
/
第5课时
《两个直角三角形全等的判定》提高练习
一、选择题
1.两个锐角分别相等的两个直角三角形( )全等.
A.不一定 B.一定不 C.一定 D.以上都不对
2.下列条件不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.一条直角边和它所对的锐角对应相等
D.一个锐角和锐角所对的直角边对应相等
3.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
/
A.SSS B.AAS C.SAS D.HL
4.如果两个直角三角形的两条直角边对应相等,那么这两个直角三角形全等的依据是( )
A.SSS B.AAS C.SAS D.HL
5.如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( )/
A.8 B.5 C.3 D.2
二、填空题
6.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4.直线l上有一点C在点P右侧,PC=4cm,过点C作射线CD⊥l,点F为射线CD上的一个动点,连结AF.当△AFC与△ABQ全等时,AQ= cm.
/
7.两个直角三角形中,如果都有一个锐角等于38°,又都有一条边等于3.8cm,那么这两个直角三角形 全等(填“一定”或“不一定”).
8.已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL)./
三、解答题
9.如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.求证:CE=BF.
/
10.如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
/
第6课时
《全等三角形的判定方法的综合》提高练习
一、选择题
1.如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E,下列说法错误的是( )
/
A.AD=BC B.∠DAB=∠CBA C.△ACE≌△BDE D.AC=CE
2.如图,已知△ABC中,AB=AC,BD=CD,则下列结论中错误的是( )
/
A.∠B=∠C B.∠BAC=∠C C.AD⊥BC D.∠BAD=∠CAD
3.如图,AB=AD,CB=CD,∠B=30°,∠BAD=50°,则∠BCD的度数是( )
/
A.110° B.100° C.120° D.80°
4.如图,已知AB=AC,BD=CD,E是AD上的一点,则下列结论中不成立的是( )
/
A.BE=CE B.AE=DE C.∠BAD=∠CAD D.∠BED=∠CED
5.如图,把两个含有45°角的直角三角板放置在桌面上,点E在BC上,AE的延长线与CD交于点F,则∠AFD( )
/
A.是锐角 B.是直角 C.是钝角 D.度数不能确定
二、填空题
6.如图,∠ADC= °.
/
7.把等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点H的坐标为(0,2),另一个顶点G的坐标为(6,6),则点K的坐标为 .
/
8.如图1,△ABC中,AD是∠BAC的角平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路:
/
(1)判定△ABD与△AED全等的依据是 (SSS,SAS,ASA,AAS从其中选择一个);
(2)∠ACB与∠ABC的数量关系为: .
三、解答题
9.如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G,H,若AB=CD,求证:AG=DH.
/
10.如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:∠C=∠D.
/
参考答案
第1课时
1.解:以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出三个三角形△ABG,△ABM,△ABH和原三角形全等.
所以可画出6个.
故选:B.
/
2.解:∵AO=BO,OC=OD,∠O=∠O
∴△ADO≌△BCO(SAS),故②正确;
∴∠COP=∠DOP
∵OC=OD,OP=OP
∴△OCP≌△ODP(SAS),故④正确;
∴PC=PD
∵∠CAP=∠DBP,∠CPA=∠DPB
∴△APC≌△BPD(AAS),故①正确;
∴PA=PB
∵AO=BO,OP=OP
∴△AOP≌△BOP(SSS),故③正确.
故选:A.
3.解:补充∠EAD=∠BAC,
∵∠EAD=∠BAC,
∴∠EAD+∠DAC=∠BAC+∠DAC,
即∠EAC=∠DAB,
在△AEC和△ADB中M
/,
∴△ABD≌△ACE(SAS).
故选:A.
4.解:∵△ABC与△DCE都是等边三角形
∴BC=AC,CE=CD,∠ACB=∠DCE=60°
∴∠ACD=60°
∴∠ACE=∠BCD=120°
∴△ACE≌△BCD
故选:C.
5.解:补充BF=EC,理由如下:
∵BF=EC,
∴BC=EF,
在△ABC和△DEF中,/,
∴△ABC≌△DEF(SAS),
故选:D.
6.解:△ABE≌△ACD,
理由是:∵AD=AE,BD=CE,
∴AB=AC,
在△ABE和△ACD中
/
∴△ABE≌△ACD(SAS),
∴∠B=∠C,
故答案为:△ABE,△ACD,SAS.
7.解:∵AD∥BC,
∴∠DAC=∠BCA,
在△ABC和△CDA,
/,
∴△ABC≌△CDA(SAS),
故答案为:AD=CB.
8.解:添加的一个条件∠C=∠B,
∵在△ACD和△ABE中/,
∴△ABE≌△ACD(ASA);
添加条件AE=AD,
∵在△ACD和△ABE中/,
∴△ABE≌△ACD(SAS),
故答案为:∠C=∠B;AE=AD.
9.解:(1)△ADB≌△ADC,
理由:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ADB和△ADC中,
/,
∴△ADB≌△ADC(SAS),
(2)AD⊥BC;
理由:∵△ADB≌△ADC,
∴∠ADB=∠ADC,
∴∠ADB=∠ADC=90°,
∴AD⊥BC.
10.解:
全等,理由如下:
∵AE=CF,
∴AF=CE,
∵DF∥BE,
∴∠DFE=∠BEF,
∴∠AFD=∠BEC,
在△AFD和△CEB中
/
∴△AFD≌△BEC(SAS).
第2课时
1.解:由图形可知该三角形的两角及其夹边是确定的,
∴可利用ASA画一个和该三角形全等的三角形,
故选:C.
2.解:∵AF=CD
∴AC=DF
又∵∠A=∠D,∠1=∠2
∴△ABC≌△DEF
∴AC=DF,
∴AF=CD
故选:D.
/
3.解:在△DEB与△CEA中,
/,
∴△DEB≌△CEA(ASA)
∴BE=EA,
∴AD=BC,
在△OAD与△OCB中,
/,
∴△OAD≌△OBC,
∴∠OAD=∠OBC,OA=OB,
故选:B.
4.证明:∠ADC=∠2+∠ADE=∠ABD+∠1
∴∠ABD=∠ADE,
又∵AB=AD,
∴如∠ACB=∠AED,
则△ABC≌△ADE(AAS)
故答案为:∠ACB=∠AED或BC=DE或∠1=∠DAE.
5.解:BD=CD,
理由是:∵在△ABD和△ACD中
/
∴△ABD≌△ACD(SAS),
故答案为:BD=CD.
6.解:补充的条件是AE=AD,
∵在△ABD和△ACE中/,
∴△ABD≌△ACE(SAS),
故答案为:AE=AD.
7.解:添加条件:∠B=∠E;
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ACB=∠DCE,
在△ABC和△DEC中,
/
∴△ABC≌△DEC(ASA).
故答案为:∠B=∠E
8.证明:∵∠BAE=∠BCE=∠ACD=90°,
∴∠DCE+∠ECA=∠ECA+∠ACB,
∴∠DCE=∠ACB,且∠B+∠CEA=180°,
又∠DEC+∠CEA=180°,
∴∠B=∠DEC,
在△ABC和△DEC中
/
∴△ABC≌△DEC(ASA).
9.证明:∵EF∥BC,PG∥AB,
∴∠C=∠AFE,∠GPC=∠A,
又AP=CF,
∴AP+PF=CF+PF,
∴AF=PC,
∴由/,得△AEF≌△PGC.
10.证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中
/
∴△ABC≌△ADE(ASA).
第3课时
1.解:连接BC,AC,
由作图知:在△OAC和△OBC中,/
∴△OAC≌△OBC(SSS),
故选:A.
/
2.解:∵AB=AD,BC=CD,AC=AC,
∴△ABC≌△ADC(SSS),
∴∠ACB=∠ACD,
∴△BCE≌△DCE(SAS),
∴BE=DE,
∴△ABE≌△ADE(SSS).
∴全等三角形共有3对.
故选:C.
3.解:如图所示:
/,
最多可以画出4个.
故选:B.
4.解:图中的全等三角形共有3对.
∵AC=AD,CE=DE,AE公共,
∴△ACE≌△ADE.(SSS)
进而得出△CEB≌△DEB,△ABC≌△ABD;
故选:C.
5.解:∵AB=AC,BE=CD,
要使△ABE≌△ACD,依据SSS,
∴还需添加条件AE=AD即可,
故答案为AE=AD.
6.解:补充的条件是AE=AD,
∵在△ABD和△ACE中/,
∴△ABD≌△ACE(SAS),
故答案为:AE=AD.
7.解:BD=AC,∠DAB=∠CBA,
理由是:
在△ABC和△BAD中
/,
∴△ABC≌△BAD(SSS),
在△ABC和△BAD中
/,
∴△ABC≌△BAD(SAS).
故答案为:BD=AC,∠DAB=∠CBA.
8.解:添加:∠B=∠B′,
如图所示:在△ABC和△A′B′C′中
/,
∴△ABC≌△A′B′C′(SAS),∴
故答案为:∠B=∠B′.
/
9.解:连接AC,则△ABC≌△ADC,证明如下:
在△ABC与△ADC中,/,
∴△ABC≌△ADC./
10./
已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,
求证:△ABC≌△DEF.
证明:∵BC=EF,AM是△ABC的中线,DN是△DEF的中线,
∴BM=EN,
在△ABM和△DEN中,
∵/,
∴△ABM≌△DEN(SSS),
∴∠B=∠E,
在△ABC和△DEF中,
∵/,
∴△ABC≌△DEF(SAS).
第4课时
1.解:A、AB=DC,AC=DB,BC=CB,符合全等三角形的判定定理SSS,能推出△ABC≌△DCB,故本选项错误;
B、AB=DC,∠ABC=∠DCB,BC=CB,符合全等三角形的判定定理SAS,能推出△ABC≌△DCB,故本选项错误;
C、∵OB=OC,
∴∠DBC=∠ACB,
∵∠A=∠D,
∴根据三角形内角和定理得出∠ABC=∠DCB,
∠A=∠D,∠ABC=∠DCB,BC=BC,符合全等三角形的判定定理AAS,能推出△ABC≌△DCB,故本选项错误;
D、AB=DC,BC=CB,∠A=∠D不符合全等三角形的判定定理,不能推出△ABC≌△DCB,故本选项正确;
故选:D.
2.解:∵AC⊥BE,∠A=∠E,
∴如果再加BC=DC,利用ASA即可判定△ABC≌△EDC,
如果再加∠B=∠CDE,不能证明△ABC≌△EDC,
如果再加AB=DE,利用AAS即可判定△ABC≌△EDC,
同理如果加AC=CE,利用AAS即可判定△ABC≌△EDC,
故选:B.
3.解:A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意;
故选:D.
4.解:A、∵在△AOB和△DOC中
/
∴△AOB≌△DOC(ASA),正确,故本选项错误;
B、∵在△AOB和△DOC中
/
∴△AOB≌△DOC(AAS),正确,故本选项错误;
C、∵在△AOB和△DOC中
/
∴△AOB≌△DOC(AAS),正确,故本选项错误;
D、根据三个角对应相等的两个三角形不全等,错误,故本选项正确;
故选:D.
5.解:A、添加AC=BD不能判定△OAB≌△COD,故此选项错误;
B、添加OD=OC不能判定△OAB≌△COD,故此选项错误;
C、添加∠A=∠C,可利用ASA判定△OAB≌△COD,故此选项正确;
D、添加AO=BO,不能判定△OAB≌△COD,故此选项错误;
故选:C.
6.解:添加AB=AD;理由如下:
在△ABC和△ADC中,/,
∴△ABC≌△ADC;
故答案为:AB=AD(答案不唯一).
7.解:∵在△ABD和△CDB中/,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠CBD,∠ABD=∠BDC,
∵在△ABC和△CDA中/,
∴△ABC≌△CDA(SSS),
∴∠DAC=∠BCA,∠ACD=∠BAC,
∵在△AOB和△COD中/,
∴△AOB≌△COD(ASA),
∵在△AOD和△COB中/,
∴△AOD≌△COB(ASA),
故答案为:4.
/
8.解:∠A=∠E,
理由是:∵在△ABC和△EDF中
/
∴△ABC≌△EDF(AAS),
故答案为:∠A=∠E.
9.证明:∵AB∥DE,BC∥EF
∴∠A=∠EDF,∠F=∠BCA
又∵AD=CF
∴AC=DF
∴△ABC≌△DEF.(ASA)
10.证明:在△AOB和△DOC中,/,
所以,△AOB≌△DOC(AAS).
第5课时
1.解:由三个角分别相等的两个三角形不一定全等,得
两个锐角分别相等的两个直角三角形不一定全等,
故选:A.
2.解:A、两条直角边对应相等,可利用全等三角形的判定定理SAS来判定两直角三角形全等,故本选项正确;
B、两个锐角对应相等,再由两个直角三角形的两个直角相等,AAA没有边的参与,所以不能判定两个直角三角形全等;故本选项错误;
C、一条直角边和它所对的锐角对应相等,可利用全等三角形的判定定理ASA来判定两个直角三角形全等;故本选项正确;
D、一个锐角和锐角所对的直角边对应相等,可以利用全等三角形的判定定理ASA或AAS来判定两个直角三角形全等;故本选项正确;
故选:B.
3.解:∵AC∥BD,
∴∠A=∠B,
∵CE⊥AB,DF⊥AB,
∴∠AEC=∠DFB,且AC=BD,
∴在Rt△AEC和Rt△BFD中,满足AAS,
故选:B.
4.解:两边及夹角对应相等的两个三角形全等,这为“边角边”定理,简写成“SAS“.
故选:C.
5.解:∵∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,
∴∠CAE+∠ACD=∠ACD+∠BCD,
∴∠CAE=∠BCD,
又∵∠AEC=∠CDB=90°,AC=BC,
∴△AEC≌△CDB.
∴CE=BD=2,CD=AE=5,
∴ED=CD﹣CE=5﹣2=3(cm).
故选:C.
6.解:①当点A在点P左侧时,要使△AFC与△ABQ全等,
则应满足/,
∵AQ:AB=3:4,AQ=AP,PC=4cm,
设AQ=3x,AB=4x,则有4x﹣3x=4,
∴x=4,
∴AQ=12(cm),
②当点A在点P右侧时,同法可得:3x+4x=4,
∴x=/,
∴AQ=3x=/(cm)
故答案为:12或/.
7.解:当3.8cm的边一个为斜边,另一个为直角边时,两三角形不可能全等.
故答案为:不一定.
8.证明:∵在△ABE和△DCF中,
AE⊥BC,DF⊥BC,AE=DF,AB=DC,
符合直角三角形全等条件HL,
所以△ABE≌△DCF,
故填:ABE;DCF.
9.证明:∵AB⊥CD,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
/,
∴Rt△ABC≌Rt△DEF(HL).
∴BC=EF.
∴BC﹣BE=EF﹣BE.
即:CE=BF.
10.解:根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,
/
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5cm;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,
/,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=10cm,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,当P运动到AP=BC、点P与点C重合时,△ABC才能和△APQ全等.
第6课时
1.证明:在Rt△ABC和Rt△BAD中,
/,
∴Rt△ABC≌Rt△BAD(HL),
∴∠BAD=∠ABC,AD=BC,
∴AE=BE,
又∵∠C=∠D=90°,∠AEC=∠BED,
∴△ACE≌△BDE.
故选:D.
2.解:∵AB=AC,BD=CD,
∴∠B=∠C,AD⊥BC,∠BAD=∠CAD.
故A、C、D正确,B错误.
故选:B.
3.解:∵在△ABC和△ADC中,
/,
∴△ABC≌△ADC,
∴∠B=∠D=30°,∠BAC=∠DAC=/∠BAD=/×50°=25°,
∴∠ACD=∠ACB=180°﹣∠D﹣∠DAC=180°﹣30°﹣25°=125°,
∴∠BCD=360°﹣125°﹣125°=110°,
故选:A.
4.解:在△ADB和△ADC中,
/,
∴△ADB≌△ADC,
∴∠BAD=∠CAD,∠BDE=∠CDE,
在△EDC和△EDB中,
/,
∴△EDC≌△EDB,
∴BE=EC,∠BED=∠CED,
故A、C、D正确,
故选:B.
5.解:∵AB=BC,∠ABE=∠CBD=90°,BE=BD,
∴△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠AEB=∠CEF,
∴∠AFE=∠ABE=90°,
故选:B.
6.解:由作图可知∠CAD=∠BAD=/∠CAB,
∵∠C=90°,∠B=50°,
∴∠CAB=180°﹣90°﹣50°=40°,
∴∠BAD=/×40°=20°,
∴∠ADC=∠B+∠BAD=50°+20°=70°,
故答案为:70.
7.解:作GP⊥y轴,KQ⊥y轴,如图,
/
∴∠GPH=∠KQH=90°
∵GH=KH,∠GHK=90°,
∴∠GHP+∠KHQ=90°.
又∠HKQ+∠KHQ=90°
∴∠GHP=∠HKQ.
在△GPH和△HQK中,
/,
∴Rt△GPH≌Rt△KHQ(AAS),
∵KQ=PH=6﹣2=4;HQ=GP=6.
∵QO=QH﹣HO=6﹣2=4,
∴K(4,﹣4).
故答案为:(4,﹣4).
8.解:(1)SAS;
(2)∵△ABD≌△AED,
∴∠B=∠E,
∵CD=CE,
∴∠CDE=∠E,
∴∠ACB=2∠E,
∴∠ACB=2∠ABC.
故答案为:SAS,∠ACB=2∠ABC.
9.证明:∵AB∥CD、EC∥BF,
∴四边形BFCE是平行四边形,∠A=∠D,
∴∠BEC=∠BFC,BE=CF,
∴∠AEG=∠DFH,
∵AB=CD,
∴AE=DF,
在△AEG和△DFH中,
∵/,
∴△AEG≌△DFH(ASA),
∴AG=DH.
10.证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
在△ADF与△BCE中,
/
∴△ADF≌△BCE(SAS),
∴∠C=∠D.
