沪科版八年级上册数学第十四章全等三角形14.2三角形全等的判定培优练习(6课时含答案)
文档属性
| 名称 | 沪科版八年级上册数学第十四章全等三角形14.2三角形全等的判定培优练习(6课时含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 226.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-11 07:12:03 | ||
图片预览




文档简介
14.2.1《三角形全等的判定》培优练习
第1课时《SAS》
一、选择题
1.下列条件中,满足△ABC≌△A'B'C'的是( )
A.AB=A'B',AC=A'C',∠B=∠B' B.AB=A'B',BC=B'C',∠A=∠A'
C.AC=A'C',BC=B'C',∠C=∠C' D.AC=A'C',BC=B'C',∠B=∠B'
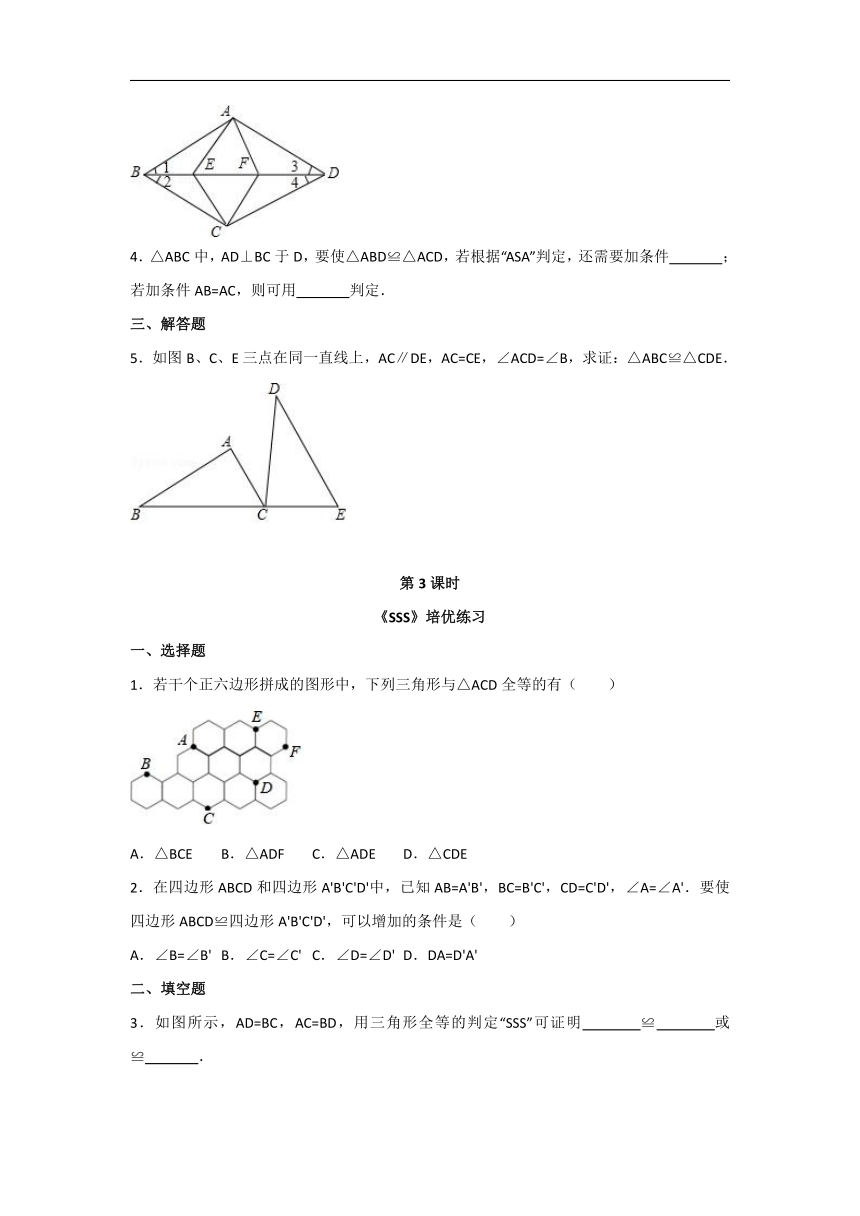
2.如图,AB=12m,CA⊥AB于A,DB上AB于B,且AC=4m.点P从点B向点A运动,每分走1m;点Q从点B向点D运动,每分走2m.P,Q两点同时出发,运动( )min后,△CAP≌△PBQ.
A.2 B.3 C.4 D.5
二、填空题
3.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从点B以1m/min的速度向点A运动;点Q从点B以2m/min的速度向点D运动,P,Q两点同时出发,运动 min后,△CAP≌△PBQ.
4.如图,AB与CD相交于点E,AE=CE,如果根据“SAS”可以判定△ADE≌△CBE,那么只需要补充一个条件 .
三、解答题
5.如图,AB=DB,BC=BE,∠1=∠2,试说明△ABE≌△DBC.
第2课时
《ASA》培优练习
一、选择题
1.如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
A.∠B=∠C B.∠D=∠E C.∠BAC=∠EAD D.∠B=∠E
2.如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )
A.8对 B.4对 C.2对 D.1对
填空题
3.如图,∠1=∠2,∠3=∠4,则图中全等三角形有 对.
4.△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“ASA”判定,还需要加条件 ;若加条件AB=AC,则可用 判定.
三、解答题
5.如图B、C、E三点在同一直线上,AC∥DE,AC=CE,∠ACD=∠B,求证:△ABC≌△CDE.
第3课时
《SSS》培优练习
一、选择题
1.若干个正六边形拼成的图形中,下列三角形与△ACD全等的有( )
A.△BCE B.△ADF C.△ADE D.△CDE
2.在四边形ABCD和四边形A'B'C'D'中,已知AB=A'B',BC=B'C',CD=C'D',∠A=∠A'.要使四边形ABCD≌四边形A'B'C'D',可以增加的条件是( )
A.∠B=∠B' B.∠C=∠C' C.∠D=∠D' D.DA=D'A'
二、填空题
3.如图所示,AD=BC,AC=BD,用三角形全等的判定“SSS”可证明 ≌ 或 ≌ .
4.在平面直角坐标系中,点A(1,2),B(6,5),C(5,2),存在点E,使△AEC和△ABC全等,写出所有满足条件的E点的坐标 .
三、解答题
5.如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.
第4课时
《其他判定两个三角形全等的条件》培优练习
一、选择题
1.如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
A.4 组 B.3 组 C.2 组 D.1 组
2.如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A.相等 B.不相等 C.互余或相等 D.互补或相等
二、填空题
3.如图,AB∥CD,AD∥BC,图中全等三角形共有 对.
4.如图,AB=AC,若利用“ASA”来说明△ABE≌△ACD,则还需补充的条件是 ;若利用“AAS”来说明△ABE≌△ACD,则还需补充的条件是 .
三、解答题
5.如图,已知AD∥CE,∠1=∠2.
(1)试说明AB∥CD;
(2)若点D为线段BE中点,试说明△ABD≌△CDE.
第5课时
《两个直角三角形全等的判定》培优练习
一、选择题
1.在平面直角坐标系内,点O为坐标原点,A(﹣4,0),B(0,3).若在该坐标平面内有以点P(不与点A、B、O重合)为一个顶点的直角三角形与Rt△ABO全等,且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的三角形个数为( )
A.9 B.7 C.5 D.3
2.如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,则图中全等的直角三角形有( )
A.3对 B.4对 C.5对 D.6对
二、填空题
3.如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动 秒时,△DEB与△BCA全等.
4.已知Rt△ABC的两直角边不相等,如果要画一个三角形与Rt△ABC全等,且使所画三角形两条直角边与Rt△ABC的两条直角边分别在同一条直线上(Rt△ABC本身不算),那么满足上述条件的三角形最多能画出 个.
三、解答题
5.(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.
第6课时
《全等三角形的判定方法的综合》培优练习
一、选择题
1.小明用五根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )
A.∠A=∠C B.∠ABC=∠CDA C.∠ABD=∠CDB D.∠ABD=∠C
2.如图,在△ABC中,AB=AC,点D是△ABC外一点,连接AD、BD、CD,且BD交AC于点O,在BD上取一点E,使得AE=AD,∠EAD=∠BAC.若∠ACB=70°,则∠BDC的度数为( )
A.30° B.40° C.50° D.60°
二、填空题
3.如图,把△ABC的中线CD延长到E,使DE=CD,连接AE,若AC=4且△BCD的周长比△ACD的周长大1,则AE= .
4.如图,在平面直角坐标系中,已知点A(0,3),点B(9,0),且∠ACB=90°,CA=CB,则点C的坐标为 .
三、解答题
5.如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.
参考答案
第1课时
1.解:AB=A'B',AC=A'C',∠B=∠B',不符合SAS,选项A不满足△ABC≌△A'B'C';
AB=A'B',BC=B'C',∠A=∠A',不符合SAS,选项B不满足△ABC≌△A'B'C';
AC=A'C',BC=B'C',∠C=∠C',符合SAS,选项C满足△ABC≌△A'B'C';
AC=A'C',BC=B'C',∠B=∠B',不符合SAS,选项D不满足△ABC≌△A'B'C'.
故选:C.
2.解:设t min后△CAP≌△PBQ,
由题意的,AP=AB﹣BP=12﹣t,BQ=2t,
当△CAP≌△PBQ时,AP=BQ,即12﹣t=2t,
解得:t=4,
即4 min后△CAP≌△PBQ.
故选:C.
3.解:设t min后△CAP≌△PBQ,
由题意的,AP=AB﹣BP=12﹣t,BQ=2t,
当△CAP≌△PBQ时,AP=BQ,即12﹣t=2t,
解得:t=4,
即4 min后△CAP≌△PBQ.
故答案为:4.
4.解:需要补充条件DE=BE,
∵在△DAE和△BCE中,
∴△ADE≌△CBE(SAS),
故答案为:DE=BE.
5.证明:∵∠1=∠2,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS).
第2课时
1.解:∠BAC=∠EAD,
理由是:∵∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,
∴∠BAE=∠CAD,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
选项A、选项B,选项D的条件都不能推出△ACD≌△ABE,只有选项C的条件能推出△ACD≌△ABE,
故选:C.
2.解:∵AB∥CD,AD∥BC,
∴∠CAD=∠ACB,∠BDA=∠DBC,∠BAC=∠DCA,∠ABD=∠CDB,
又∵AC、BD为公共边,
∴△ACD≌△CAB、△BAD≌△DCB(ASA);
∴AD=BC,AB=CD,
∴△AOD≌△COB、△AOB≌△COD(ASA).
所以全等三角形有:△AOD≌△COB、△AOB≌△COD、△ACD≌△CAB、△BAD≌△DCB,共4对;故选B.
3.解:连接AC,∵∠1=∠2,BD=BD,∠3=∠4,
∴△ABD≌△CBD(ASA),
∴AB=BC,
∵∠1=∠2,BE=BE,
∴△ABE≌△CBE,(SAS),
∵∠3=∠4,
∴△ADF≌△CDF,
同理,△AED≌△CED,
△ABF≌△CBF,
△ABD≌△CBD.
△AEF≌△CEF 所以共有6对
故答案为:6.
4.解:△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“ASA”判定,还需要加条件∠DAB=∠DAC.
理由:∵∠BAD=∠CAD,AD=AD,∠ADB=∠ADC,
∴△ABD≌△ACD(ASA).
若添加AB=AC,则全等的理由是HL,
故答案为∠BAD=∠CAD,HL.
5.证明:∵AC∥DE,
∴∠ACB=∠E,∠ACD=∠D,
∵∠ACD=∠B,
∴∠D=∠B,
在△ABC和△EDC中
,
∴△ABC≌△CDE(AAS).
第3课时
1.解:根据图象可知△ACD和△ADE全等,
理由是:∵根据图形可知AD=AD,AE=AC,DE=DC,
在△ACD和△AED中,
,
∴△ACD≌△AED(SSS),
故选:C.
2.解:添加的条件是DA=D′A′.连接BD,B′D′,
∵在△ABD和△A′B′D′中
,
∴△ABC≌△A′B′C′(SAS),
∴∠ABD=∠A′B′D′,∠ADB=∠A′D′B′,BD=B′D′,
在△BCD和△B′C′D′
,
∴△ACD≌△A′C′D′(SSS),
∴∠DBC=∠D′B′C′,∠C=∠C′,∠BDC=∠B′D′C′
∴∠ABC=∠A′B′C′,∠ADC=∠A′D′C′,
∴四边形ABCD≌四边形A′B′C′D′,
故选:D.
3.解:在△ACD和△BDC中,,
∴△ACD≌△BDC(SSS);
在△ABD和△BAC中,,
∴△ABD≌△BAC(SSS).
故答案为:△ACD;△BDC;△ABD;△BAC.
4.解:如图所示:有3个点,△ACE和△ACB全等,
点E的坐标是:(0,5),(0,﹣1),(6,﹣1),
故答案为:(0,5)或(0,﹣1)或(6,﹣1).
5.△ABC≌△AED,
证明:∵BD=CE,
∴BC=ED,
在△ABC和△AED中,
,
∴△ABC≌△AED.
第4课时
1.解:第①组AB=DE,∠B=∠E,∠C=∠F,满足AAS,能证明△ABC≌△DEF.
第②组AB=DE,∠B=∠E,BC=EF满足SAS,能证明△ABC≌△DEF.
第③组∠B=∠E,BC=EF,∠C=∠F满足ASA,能证明△ABC≌△DEF.
所以有3组能证明△ABC≌△DEF.
故选:B.
2.解:第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,AC=AC′,高CD=C′D′,
∴∠ADC=∠AD′C′,
在Rt△ACD和Rt△AC′D′中,
,
Rt△ACD≌Rt△AC′D′(HL),
∴∠CAD=∠C′AD′,
此时,∠CAB+∠C′AB=180°,
是互补关系,
综上所述,这两个三角形的第三条边所对的角的关系是“相等或互补”.
故选:D.
3.解:∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).
故图中的全等三角形共有4对.
故答案为4.
4.解:∵∠A=∠A,AB=AC,
∴只需补充∠B=∠C,即可利用“ASA”来说明△ABE≌△ACD.
∵∠A=∠A,AB=AC,
∴只需补充∠AEB=∠ADC,即可利用“AAS”来说明△ABE≌△ACD.
故答案为:∠B=∠C;∠AEB=∠ADC.
5.解:(1)∵AD∥CE,
∴∠ADC=∠2,
∵∠1=∠2,
∴∠ADC=∠1,
∴AB∥CD;
(2)∵AD∥CE,
∴∠ADB=∠CED,
∵D 是BE中点,
∴BD=DE,
在△ABD和△CDE中,
∴△ABD≌△CDE(AAS).
第5课时
1.解:如图:分别以OA、OB、AB为边作与Rt△ABO全等的三角形各有3个,
则所有符合条件的三角形个数为9.
故选:A.
2.解:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
∵AC=AB,
∵∠CAE=∠BAD,
∴△AEC≌△ADB;
∴CE=BD,
∵AC=AB,
∴∠CBE=∠BCD,
∵∠BEC=∠CDB=90°,
∴△BCE≌△CBD;
∴BE=CD,
∴AD=AE,
∵AO=AO,
∴△AOD≌△AOE;
∵∠DOC=∠EOB,
∴△COD≌△BOE;
∴OB=OC,
∵AB=AC,
∴CF=BF,AF⊥BC,
∴△ACF≌△ABF,△COF≌△BOF.
∵∠ABO=∠ACO
共6对,故选D.
3.解:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=4,
∴BE=4,
∴AE=8﹣4=4,
∴点E的运动时间为4÷2=2(秒);
②当E在BN上,AC=BE时,
∵AC=4,
∴BE=4,
∴AE=8+4=12,
∴点E的运动时间为12÷2=6(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=8+8=16,
点E的运动时间为16÷2=8(秒),
故答案为:0,2,6,8.
4.解:如图所示:
△AMC,△EFC,△EGC,△HGC,△HFC,△BCN,△MNC共7个,
故答案为:7.
5.解:(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD=DE﹣CE;
∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∴∠ABD+∠DAB=∠DAB+∠CAE,
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴AD+AE=BD+CE,
∵DE=BD+CE,
∴BD=DE﹣CE.
第6课时
1.解:∵AB=CD,AD=CB
又BD=DB
∴△ABD≌△CDB
∴∠A=∠C,∠ABD=∠CDB;
又∠ABD=∠CDB,∠CBD=∠ADB
∴∠ABC=∠CDA,
∠ABD与∠C不是对应角不相等.
故选:D.
2.解:∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
∴△ABE≌△ACD (SAS)
∴∠ABD=∠ACD.
∵∠BOC是△ABO和△DCO的外角
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴∠ABD+∠BAC=∠ACD+∠BDC
∴∠BAC=∠BDC
∵∠ACB=65°,AB=AC
∴∠ABC=∠ACB=70°
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°
∴∠BDC=∠BAC=40°.
故选:B.
3.解:∵CD为△ABC的中线,
∴AD=BD,
在△ADE和△BDE中
,
∴△ADE≌△BDE,
∴AE=BC,
∵△BCD的周长比△ACD的周长大1,
∴CD+BD+BC=AC+AD+CD+1,
∴BC=AC+1=4+1=5,
∴AE=5.
故答案为5.
4.解:如图,过点C作CE⊥OA,CF⊥OB,
∵∠AOB=90°,
∴四边形OECF是矩形,
∴∠ECF=90°,
∵∠ACB=90°,
∴∠ACE=∠BCE
在△ACE和△BCF中,,
∴△ACE≌△BCF,
∴CE=CF,
∵四边形OECF是矩形,
∴矩形OECF是正方形,
∴OE=OF,
∵AE=OE﹣OA=OE﹣3,BF=OB﹣OF=9﹣OF,
∴OE=OF=6,
∴C(6,6),
故答案为:(6,6);
5.解:(1)BF=AC,理由是:
如图1,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEF=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠AFE=∠BFD,
∴∠DAC=∠EBC,
在△ADC和△BDF中,
∵,
∴△ADC≌△BDF(AAS),
∴BF=AC;
(2)NE=AC,理由是:
如图2,由折叠得:MD=DC,
∵DE∥AM,
∴AE=EC,
∵BE⊥AC,
∴AB=BC,
∴∠ABE=∠CBE,
由(1)得:△ADC≌△BDF,
∵△ADC≌△ADM,
∴△BDF≌△ADM,
∴∠DBF=∠MAD,
∵∠DBA=∠BAD=45°,
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,
即∠ABE=∠BAN,
∵∠ANE=∠ABE+∠BAN=2∠ABE,
∠NAE=2∠NAD=2∠CBE,
∴∠ANE=∠NAE=45°,
∴AE=EN,
∴EN=AC.
