湘教版八年级数学上册第2章三角形《2.3 等腰三角形》教学课件(共33张)
文档属性
| 名称 | 湘教版八年级数学上册第2章三角形《2.3 等腰三角形》教学课件(共33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-11 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
等腰三角形
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
我们欣赏如图所示两个建筑物,在图中我们可以发现什么样的特殊三角形呢?这样的三角形我们又是怎样定义的呢?它们有什么性质呢?
我发现这两个三角形好像有两条边是相等的。
对于这种有两条边相等的三角形,我们称其为何种三角形呢?让我们一起来探究吧!
02 新知探究
新知探究
概念学习
有两条边相等的三角形叫做等腰三角形.
A
C
B
底角
底角
顶角
腰
腰
底边
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
新知探究
等腰三角形的性质
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
等腰三角形的两底角相等(“等边对等角”).
新知探究
练一练
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、
钝角都可以.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.
(X)
(X)
(X)
(√)
(X)
(√)
新知探究
练一练
2. 等腰三角形的一个内角是50°,求这个三角形的底角的度数.
解:当50°的角是底角时,三角形的底角就是50°;
当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
新知探究
等边三角形的性质
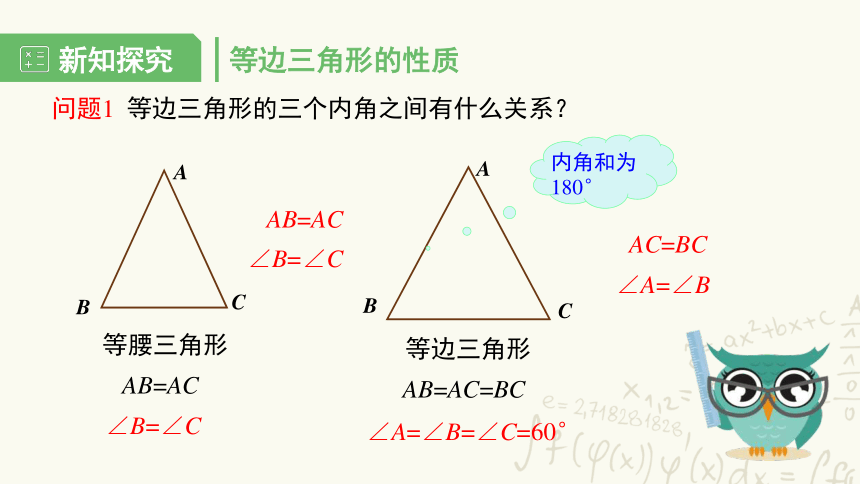
问题1 等边三角形的三个内角之间有什么关系?
A
B
C
A
B
C
等腰三角形
AB=AC
∠B=∠C
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
∠A=∠B=∠C=60°
内角和为180°
AC=BC
∠A=∠B
新知探究
等边三角形的性质
性质: 等边三角形的三个内角相等,且都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
新知探究
练一练
如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE, ∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
方法总结:等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合”等边对等角”、三角形的内角和与外角的性质.
新知探究
等腰三角形的判断
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
做一做:画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?
C
A
B
AB=AC
你能验证你的结论吗?
新知探究
等腰三角形的判定
等腰三角形的判定方法
有两个角相等的三角形是等腰三角形
(简称“等角对等边”).
应用格式:
在△ABC中,
∵∠B=∠C, ( )
∴ AC=AB. ( )
即△ABC为等腰三角形.
已知
等角对等边
B
C
A
(
(
新知探究
练一练
已知:如图,在△ABC中,AB=AC,点D,E分别是 AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.
证明: ∵AB=AC,
∴ ∠B=∠C.
又∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
∴ ∠ADE=∠AED.
∴ △ADE为等腰三角形.
新知探究
等边三角形的判定
由等腰三角形的判定定理可以直接得到:
定理1:三个角都是60°的三角形是等边三角形.
定理2:有一个角是60°的等腰三角形是等边三角形.
新知探究
练一练
根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(3)
(4)
(5)
(6)
不
是
是
是
不一定
是
是
是
03 典型例题
例题讲解
1. 等腰三角形有一个角是90°,则另两个角的度数分别是 ( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
2. 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
例题讲解
3.如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为20°,则∠α的度数为( )
A.60° B.45° C.40° D.30°
C
例题讲解
4.(1)等腰三角形一个底角为75°,它的另外两个角为
____ __;
(2)等腰三角形一个角为36°,它的另外两个角为
____________________;
(3)等腰三角形一个角为120°,它的另外两个角为
.
75°, 30°
72°,72°或36°,108°
30°,30°
例题讲解
5.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBA=_____,∠BDC=_____,图中的等腰三角形有_______________________.
A
B
C
D
36°
72°
△ABC、
△DBA、
△BCD
例题讲解
6.如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.
A
C
B
D
E
12
例题讲解
7.在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数是( )
A.10° B.15°
C.20° D.25°
B
04 拓展提高
拓展提高
1.如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 30°,求 ∠BAD 和 ∠ADC的度数.
A
B
C
D
解:∵AB=AC,D是BC边上的中点,
∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°.
∴∠ BAC =180° - 30°-30° = 120°.
= 60°.
拓展提高
2.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE (等角对等边).
05 课堂小结
课堂小结
等腰三角形的性质
等边对等角
三线合一
推论
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
等边三角形三个内角相等,且均等于60°
课堂小结
等腰(边)三角形的判定
等腰三角形的判定
等边三角形的判定
等角对等边
注意是指同一个三角形中
1.三个角都是60°的三角形是等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.
06 作业布置
完成课本习题 2.3 A、B组
作业布置
谢 谢 观 看
等腰三角形
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
我们欣赏如图所示两个建筑物,在图中我们可以发现什么样的特殊三角形呢?这样的三角形我们又是怎样定义的呢?它们有什么性质呢?
我发现这两个三角形好像有两条边是相等的。
对于这种有两条边相等的三角形,我们称其为何种三角形呢?让我们一起来探究吧!
02 新知探究
新知探究
概念学习
有两条边相等的三角形叫做等腰三角形.
A
C
B
底角
底角
顶角
腰
腰
底边
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
新知探究
等腰三角形的性质
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
等腰三角形的两底角相等(“等边对等角”).
新知探究
练一练
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、
钝角都可以.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.
(X)
(X)
(X)
(√)
(X)
(√)
新知探究
练一练
2. 等腰三角形的一个内角是50°,求这个三角形的底角的度数.
解:当50°的角是底角时,三角形的底角就是50°;
当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
新知探究
等边三角形的性质
问题1 等边三角形的三个内角之间有什么关系?
A
B
C
A
B
C
等腰三角形
AB=AC
∠B=∠C
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
∠A=∠B=∠C=60°
内角和为180°
AC=BC
∠A=∠B
新知探究
等边三角形的性质
性质: 等边三角形的三个内角相等,且都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
新知探究
练一练
如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE, ∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
方法总结:等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合”等边对等角”、三角形的内角和与外角的性质.
新知探究
等腰三角形的判断
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
做一做:画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?
C
A
B
AB=AC
你能验证你的结论吗?
新知探究
等腰三角形的判定
等腰三角形的判定方法
有两个角相等的三角形是等腰三角形
(简称“等角对等边”).
应用格式:
在△ABC中,
∵∠B=∠C, ( )
∴ AC=AB. ( )
即△ABC为等腰三角形.
已知
等角对等边
B
C
A
(
(
新知探究
练一练
已知:如图,在△ABC中,AB=AC,点D,E分别是 AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.
证明: ∵AB=AC,
∴ ∠B=∠C.
又∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
∴ ∠ADE=∠AED.
∴ △ADE为等腰三角形.
新知探究
等边三角形的判定
由等腰三角形的判定定理可以直接得到:
定理1:三个角都是60°的三角形是等边三角形.
定理2:有一个角是60°的等腰三角形是等边三角形.
新知探究
练一练
根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(3)
(4)
(5)
(6)
不
是
是
是
不一定
是
是
是
03 典型例题
例题讲解
1. 等腰三角形有一个角是90°,则另两个角的度数分别是 ( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
2. 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
例题讲解
3.如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为20°,则∠α的度数为( )
A.60° B.45° C.40° D.30°
C
例题讲解
4.(1)等腰三角形一个底角为75°,它的另外两个角为
____ __;
(2)等腰三角形一个角为36°,它的另外两个角为
____________________;
(3)等腰三角形一个角为120°,它的另外两个角为
.
75°, 30°
72°,72°或36°,108°
30°,30°
例题讲解
5.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBA=_____,∠BDC=_____,图中的等腰三角形有_______________________.
A
B
C
D
36°
72°
△ABC、
△DBA、
△BCD
例题讲解
6.如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.
A
C
B
D
E
12
例题讲解
7.在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数是( )
A.10° B.15°
C.20° D.25°
B
04 拓展提高
拓展提高
1.如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 30°,求 ∠BAD 和 ∠ADC的度数.
A
B
C
D
解:∵AB=AC,D是BC边上的中点,
∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°.
∴∠ BAC =180° - 30°-30° = 120°.
= 60°.
拓展提高
2.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE (等角对等边).
05 课堂小结
课堂小结
等腰三角形的性质
等边对等角
三线合一
推论
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
等边三角形三个内角相等,且均等于60°
课堂小结
等腰(边)三角形的判定
等腰三角形的判定
等边三角形的判定
等角对等边
注意是指同一个三角形中
1.三个角都是60°的三角形是等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.
06 作业布置
完成课本习题 2.3 A、B组
作业布置
谢 谢 观 看
同课章节目录
