人教A版高中数学选修2-1教案 3.1.1空间向量与空间角
文档属性
| 名称 | 人教A版高中数学选修2-1教案 3.1.1空间向量与空间角 |

|
|
| 格式 | zip | ||
| 文件大小 | 147.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-13 20:29:05 | ||
图片预览

文档简介
§3.2.3空间向量与空间角
教学目标
1.使学生学会求异面直线所成的角、直线与平面所成的角、二面角的向量方法;
2.使学生能够应用向量方法解决一些简单的立体几何问题;
3.使学生的分析与推理能力和空间想象能力得到提高.
教学重点
求解二面角的向量方法
教学难点
二面角的大小与两平面法向量夹角的大小的关系
教学过程
一、复习引入
用空间向量解决立体几何问题的“三步曲”
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(化为向量问题)
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(进行向量运算)
(3)把向量的运算结果“翻译”成相应的几何意义。(回到图形)
二、知识讲解与典例分析
知识点1:面直线所成的角(范围:)
(1)定义:过空间任意一点o分别作异面直线a与b的平行线a′与b′,那么直线a′与b′ 所成的锐角或直角,叫做异面直线a与b 所成的角.
(2)用向量法求异面直线所成角
设两异面直线a、b的方向向量分别为和,
问题1: 当与的夹角不大于90°时,异面直线a、b 所成
的角与 和 的夹角的关系?
问题 2:与的夹角大于90°时,,异面直线a、b 所成的角
与 和的夹角的关系?
结论:异面直线a、b所成的角的余弦值为
思考:在正方体中,若与分别为、
的四等分点,求异面直线与的夹角余弦值?
(1)方法总结:①几何法;②向量法
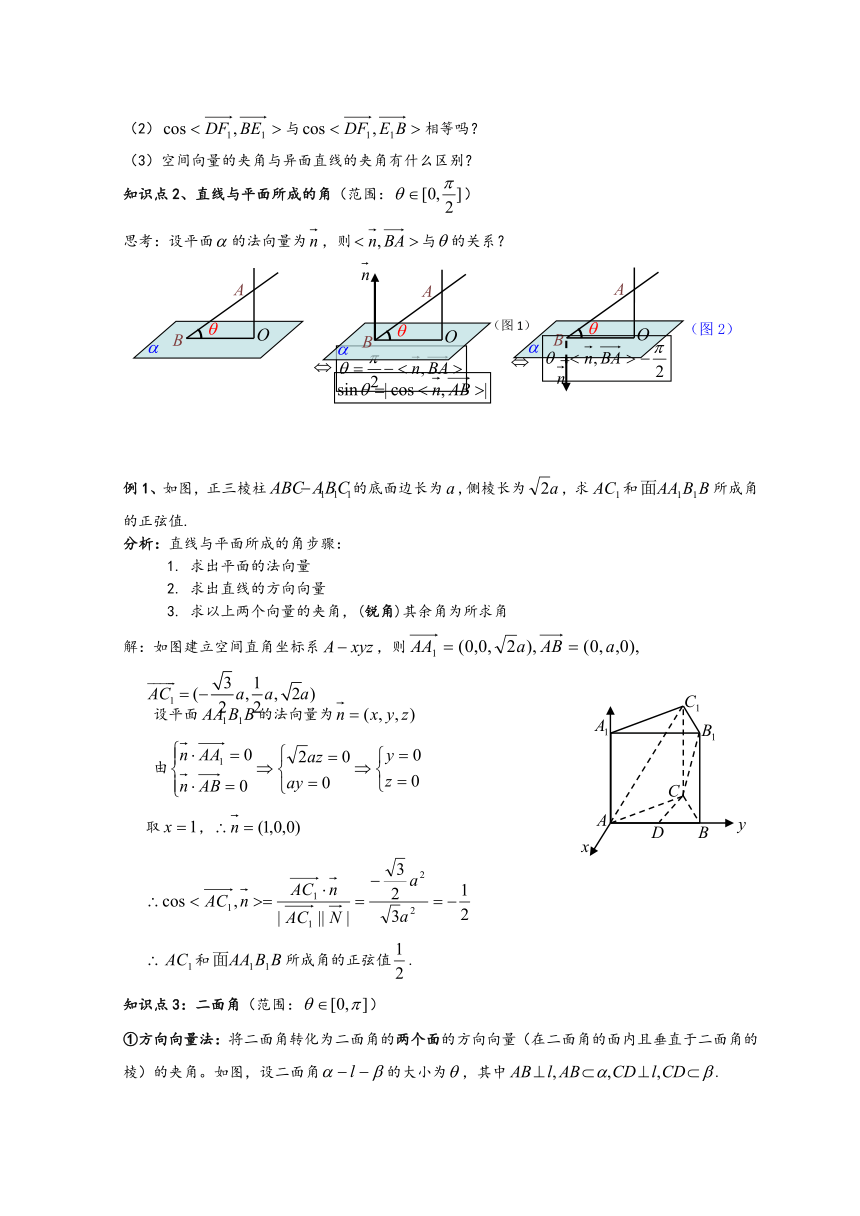
(2)与相等吗?
(3)空间向量的夹角与异面直线的夹角有什么区别?
知识点2、直线与平面所成的角(范围:)
思考:设平面的法向量为,则与的关系?
例1、如图,正三棱柱的底面边长为,侧棱长为,求和所成角的正弦值.
分析:直线与平面所成的角步骤:
1. 求出平面的法向量
2. 求出直线的方向向量
3. 求以上两个向量的夹角,(锐角)其余角为所求角
解:如图建立空间直角坐标系,则
设平面的法向量为
由
取,
和所成角的正弦值.
知识点3:二面角(范围:)
①方向向量法:将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角。如图,设二面角的大小为,其中.
结论:
②法向量法
结论: 或
归纳:法向量的方向:一进一出,二面角等于法向量夹角;同进同出,二面角等于法向量夹角的补角.
例2、如图,是一直角梯形,,面,,,求面与面所成二面角的余弦值.
解:如图建立空间直角坐标系,则
易知面的法向量为
设面的法向量为,则有
,取,得,
又方向朝面内,方向朝面外,属于“一进一出”的情况,二面角等于法向量夹角
即所求二面角的余弦值为.
练习:正方体的棱长为1,点、分别为、的中点.求二面角的余弦值。
解:由题意知,,则
设平面的法向量为,则
,取,得
又平面的法向量为
观察图形知,二面角为锐角,所以所求二面角的余弦值为
三、课堂小结
1.异面直线所成的角:
2.直线和平面所成的角:
3.二面角:.
五、布置作业
教学目标
1.使学生学会求异面直线所成的角、直线与平面所成的角、二面角的向量方法;
2.使学生能够应用向量方法解决一些简单的立体几何问题;
3.使学生的分析与推理能力和空间想象能力得到提高.
教学重点
求解二面角的向量方法
教学难点
二面角的大小与两平面法向量夹角的大小的关系
教学过程
一、复习引入
用空间向量解决立体几何问题的“三步曲”
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(化为向量问题)
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(进行向量运算)
(3)把向量的运算结果“翻译”成相应的几何意义。(回到图形)
二、知识讲解与典例分析
知识点1:面直线所成的角(范围:)
(1)定义:过空间任意一点o分别作异面直线a与b的平行线a′与b′,那么直线a′与b′ 所成的锐角或直角,叫做异面直线a与b 所成的角.
(2)用向量法求异面直线所成角
设两异面直线a、b的方向向量分别为和,
问题1: 当与的夹角不大于90°时,异面直线a、b 所成
的角与 和 的夹角的关系?
问题 2:与的夹角大于90°时,,异面直线a、b 所成的角
与 和的夹角的关系?
结论:异面直线a、b所成的角的余弦值为
思考:在正方体中,若与分别为、
的四等分点,求异面直线与的夹角余弦值?
(1)方法总结:①几何法;②向量法
(2)与相等吗?
(3)空间向量的夹角与异面直线的夹角有什么区别?
知识点2、直线与平面所成的角(范围:)
思考:设平面的法向量为,则与的关系?
例1、如图,正三棱柱的底面边长为,侧棱长为,求和所成角的正弦值.
分析:直线与平面所成的角步骤:
1. 求出平面的法向量
2. 求出直线的方向向量
3. 求以上两个向量的夹角,(锐角)其余角为所求角
解:如图建立空间直角坐标系,则
设平面的法向量为
由
取,
和所成角的正弦值.
知识点3:二面角(范围:)
①方向向量法:将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角。如图,设二面角的大小为,其中.
结论:
②法向量法
结论: 或
归纳:法向量的方向:一进一出,二面角等于法向量夹角;同进同出,二面角等于法向量夹角的补角.
例2、如图,是一直角梯形,,面,,,求面与面所成二面角的余弦值.
解:如图建立空间直角坐标系,则
易知面的法向量为
设面的法向量为,则有
,取,得,
又方向朝面内,方向朝面外,属于“一进一出”的情况,二面角等于法向量夹角
即所求二面角的余弦值为.
练习:正方体的棱长为1,点、分别为、的中点.求二面角的余弦值。
解:由题意知,,则
设平面的法向量为,则
,取,得
又平面的法向量为
观察图形知,二面角为锐角,所以所求二面角的余弦值为
三、课堂小结
1.异面直线所成的角:
2.直线和平面所成的角:
3.二面角:.
五、布置作业
