湘教版八年级数学上册第2章三角形2.5.2 全等三角形的判定教学课件(共42张)
文档属性
| 名称 | 湘教版八年级数学上册第2章三角形2.5.2 全等三角形的判定教学课件(共42张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-12 23:02:15 | ||
图片预览





文档简介
(共42张PPT)
全等三角形的判定
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
如果只满足角或边条件中的一部分,那么能保证两个三角形全等吗?
思考:
能完全重合的两个三角形全等.
什么叫全等三角形呢?
全等三角形的性质:全等三角形的对应边相等,对应角相等.
02 新知探究
新知探究
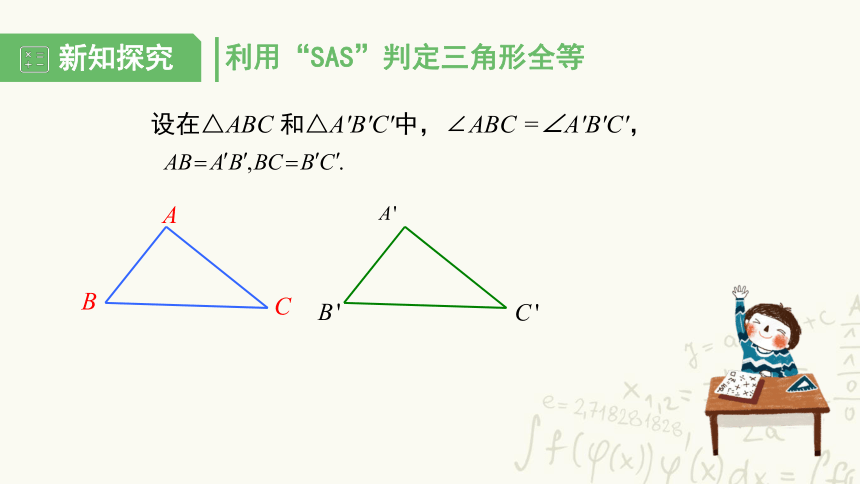
利用“SAS”判定三角形全等
设在△ABC 和△A′B′C′中,∠ABC =∠A′B′C′,
A
B
C
新知探究
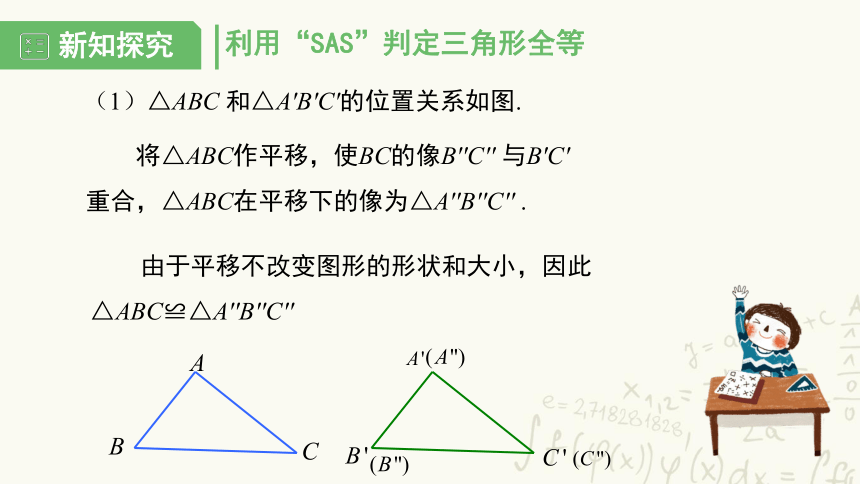
(1)△ABC 和△A′B′C′的位置关系如图.
将△ABC作平移,使BC的像B′′C′′ 与B′C′ 重合,△ABC在平移下的像为△A′′B′′C′′ .
由于平移不改变图形的形状和大小,因此△ABC≌△A′′B′′C′′
A
B
C
利用“SAS”判定三角形全等
新知探究
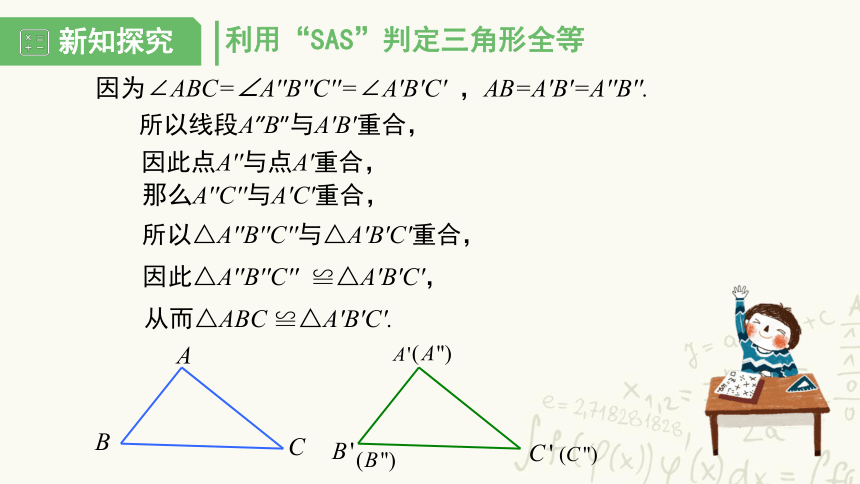
所以△A′′B′′C′′与△A′B′C′重合,
因为∠ABC=∠A′′B′′C′′=∠A′B′C′ ,AB=A′B′=A′′B′′.
所以线段A″B″与A′B′重合,
因此点A′′与点A′重合,
那么A′′C′′与A′C′重合,
因此△A′′B′′C′′ ≌△A′B′C′,
从而△ABC ≌△A′B′C′.
A
B
C
利用“SAS”判定三角形全等
新知探究
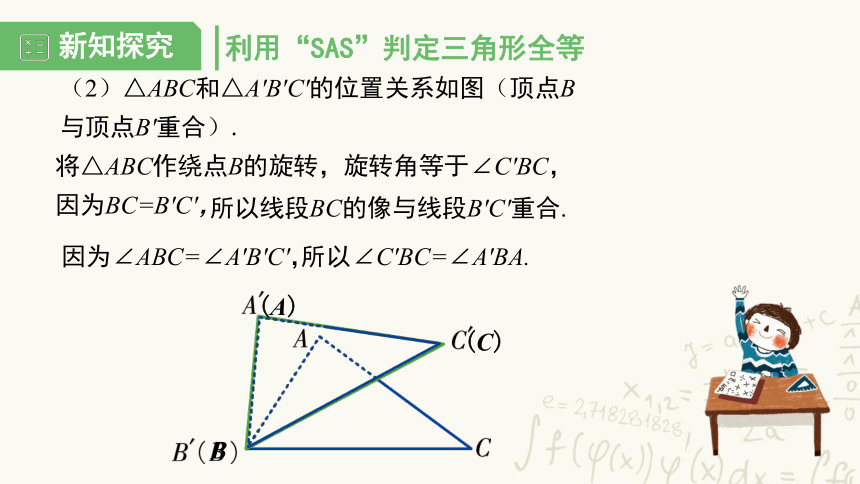
(2)△ABC和△A′B′C′的位置关系如图(顶点B 与顶点B′重合).
因为BC=B′C′,
将△ABC作绕点B的旋转,旋转角等于∠C′BC,
所以线段BC的像与线段B′C′重合.
因为∠ABC=∠A′B′C′,
所以∠C′BC=∠A′BA.
(A)
B
(C)
利用“SAS”判定三角形全等
新知探究
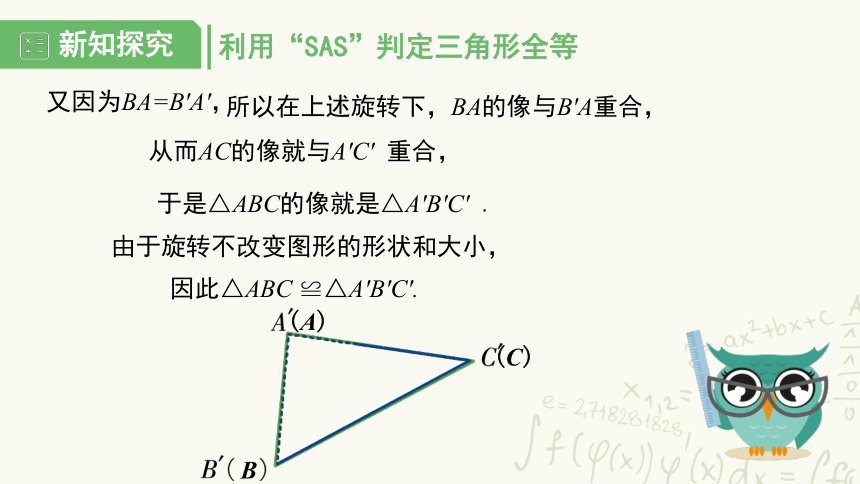
由于旋转不改变图形的形状和大小,
又因为BA=B′A′,
所以在上述旋转下,BA的像与B′A重合,
从而AC的像就与A′C′ 重合,
于是△ABC的像就是△A′B′C′ .
因此△ABC ≌△A′B′C′.
(A)
B
(C)
利用“SAS”判定三角形全等
新知探究
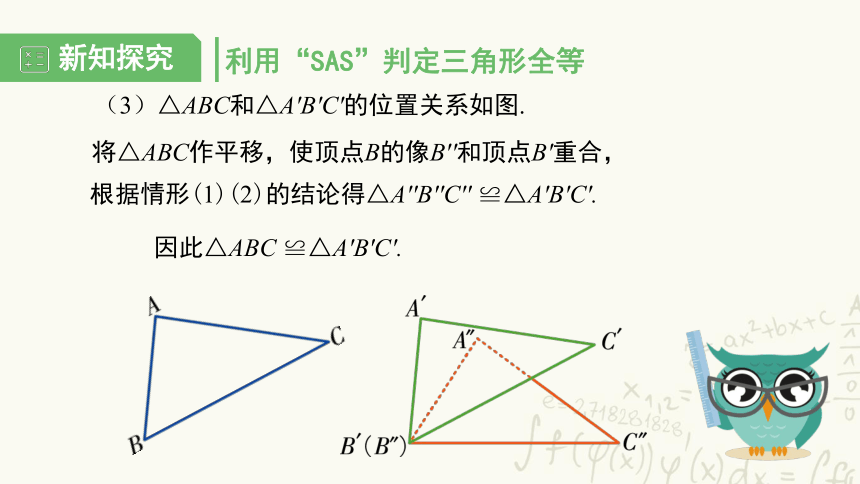
(3)△ABC和△A′B′C′的位置关系如图.
根据情形(1)(2)的结论得△A′′B′′C′′ ≌△A′B′C′.
将△ABC作平移,使顶点B的像B′′和顶点B′重合,
因此△ABC ≌△A′B′C′.
利用“SAS”判定三角形全等
新知探究
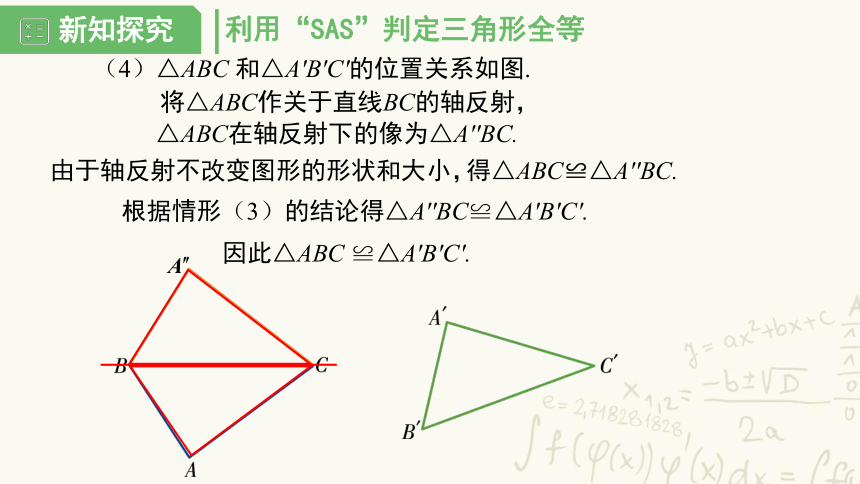
(4)△ABC 和△A′B′C′的位置关系如图.
将△ABC作关于直线BC的轴反射,
△ABC在轴反射下的像为△A′′BC.
由于轴反射不改变图形的形状和大小,
得△ABC≌△A′′BC.
根据情形(3)的结论得△A′′BC≌△A′B′C′.
因此△ABC ≌△A′B′C′.
利用“SAS”判定三角形全等
新知探究
小归纳
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
文字语言:两边和它们的夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS ”).
“边角边”判定方法
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
新知探究
如图,在△ABC和 △A′B′C′中,如果BC =B′C′,∠B=∠B′,∠C=∠C′,你能通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合吗?那么△ABC与△A′B′C′全等吗?
C'
A'
B'
B
A
C
利用“ASA”判定三角形全等
新知探究
类似于基本事实“SAS”的探究,同样地,我们可以通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合,因此△ABC ≌△A′B′C′.
利用“ASA”判定三角形全等
新知探究
“角边角”判定方法
文字语言:两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
利用“ASA”判定三角形全等
新知探究
利用“AAS”判定三角形全等
若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
60°
45°
新知探究
△ABC≌△A'B'C'.根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件.
在△ABC和 中,
∵ ∠A = ∠A′,∠B = ∠B′,
∴ ∠C =∠C′.
又∵ ,∠B=∠B′,
∴ (ASA).
利用“AAS”判定三角形全等
新知探究
归纳总结
两角分别相等且其中一组等角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
∴ △ABC≌△ A′ B′ C′ (AAS).
A
B
C
A ′
B ′
C ′
新知探究
利用“SSS”判定三角形全等
如图,在△ABC和△A′B′C′中,如果AB=A′B′,BC
= B′C′,AC= A′C′ ,那么△ABC与△A′B′C′全等吗?
如果能够说明∠A=∠A′,那么就可以由“边角边”得出△ABC≌△A′B′C′.
新知探究
由上述变换性质可知△ABC ≌ ,
则 ,
连接
将△ABC作平移、旋转和轴反射等变换,使BC的像 与 重合,并使点A的像 与点 在 的两旁,△ABC在上述变换下的像为
利用“SSS”判定三角形全等
新知探究
∴ ∠1=∠2,∠3=∠4.
从而∠1+∠3=∠2+∠4,
∵ , ,
即
在 和 中,
∴ ≌ (SAS).
∴ △ABC ≌
,
,
,
利用“SSS”判定三角形全等
新知探究
归纳总结
文字语言:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
“边边边”判定方法
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
几何语言:
新知探究
练一练
已知:如图,在△ABC中,AB=AC,点D,E
在BC上,且AD=AE,BE=CD.
求证:△ABD≌△ACE.
证明 ∵ BE = CD,
∴ BE-DE = CD-DE.
即 BD = CE.
在△ABD和△ACE中,
∴ △ABD≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
新知探究
三角形的稳定性
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
新知探究
练一练
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
下列图形中哪些具有稳定性.
03 典型例题
典型例题
1.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴ ∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,
即 AF=CE.
(已知),
(已证),
(已证),
典型例题
2. 已知:如图,△ABC≌△A′B′C′,CF,C′F′分别是∠ACB和∠A′C′B′的平分线. 求证:CF=C′F′.
证明:∵△ABC≌△A′B′C′,
∠A =∠A′ ,
∠ACB =∠A′C′B′.
∴ AC=A′C′,
∴ CF=C′F′.
又∵CF,C′F′分别是∠ACB和∠A′C′B′的平分线,
∴ ∠ACF=∠A′C′F′.
∴ △ACF≌△A′C′F′
典型例题
3. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:BD=CE.
证明: ∵BD⊥AC,CE⊥AB,
∵ 在△CDB和△BEC中,
∠ACB=∠ABC,
BC = BC ,
∴ △CDB≌△BEC(AAS).
∠CDB=∠BEC =90°,
∴ BD = CE.
∴ ∠CDB=∠BEC =90°.
典型例题
4.已知:如图 ,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)∵ AD=FB,
∴AB=FD(等式性质).
在△ABC和△FDE 中,
AC=FE(已知),
BC=DE(已知),
AB=FD(已证),
∴△ABC≌△FDE(SSS);
A
C
E
D
B
F
=
=
?
?
。
。
(2) ∵ △ABC≌△FDE(已证).
∴ ∠C=∠E(全等三角形的对应角相等).
典型例题
5.如图,AC=BD,∠CAB= ∠DBA,求证:BC=AD.
A
B
C
D
证明:在△ABC与△BAD中
AC=BD,
∠CAB=∠DBA,
AB=BA,
∴△ABC≌△BAD(SAS),
(已知)
(已知)
(公共边)
∴BC=AD
(全等三角形的对应边相等).
04 拓展提高
拓展提高
1.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
拓展提高
2.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
拓展提高
3.如图,已知AB=AE,∠1=∠2,∠B=∠E, 求证:BC=ED.
证明:∵∠1=∠2,
∴ ∠1+∠BAD=∠2+∠BAD,
即∠EAD=∠BAC.
在△AED和△ABC中,
∠E=∠B,
AE=AB,
∠EAD=∠BAC,
∴△AED≌△ABC(ASA),
∴BC=ED.
∵
A
B
E
C
D
1
2
拓展提高
4.小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流.
E
F
D
H
解:能.在△EDH和△FDH中 ,
ED=FD,(已知)
∠EDH=∠FDH,(已知)
DH=DH,(公共边)
∴△EDH≌△FDH(SAS),
∴EH=FH.(全等三角形对应边相等)
05 课堂小结
课堂小结
判定三角形全等的思路
已知两边
已知一边一角
已知两角
找夹角(SAS)
找另一边(SSS)
找任一角(AAS)
边为角的对边
边为角的一边
找夹角的另一边(SAS)
找边的对角(AAS)
找夹角的另一角(ASA)
找夹边(ASA)
找除夹边外的任意一边(AAS)
06 作业布置
完成课本习题 2.5 A、B组
作业布置
谢 谢 观 看
全等三角形的判定
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
如果只满足角或边条件中的一部分,那么能保证两个三角形全等吗?
思考:
能完全重合的两个三角形全等.
什么叫全等三角形呢?
全等三角形的性质:全等三角形的对应边相等,对应角相等.
02 新知探究
新知探究
利用“SAS”判定三角形全等
设在△ABC 和△A′B′C′中,∠ABC =∠A′B′C′,
A
B
C
新知探究
(1)△ABC 和△A′B′C′的位置关系如图.
将△ABC作平移,使BC的像B′′C′′ 与B′C′ 重合,△ABC在平移下的像为△A′′B′′C′′ .
由于平移不改变图形的形状和大小,因此△ABC≌△A′′B′′C′′
A
B
C
利用“SAS”判定三角形全等
新知探究
所以△A′′B′′C′′与△A′B′C′重合,
因为∠ABC=∠A′′B′′C′′=∠A′B′C′ ,AB=A′B′=A′′B′′.
所以线段A″B″与A′B′重合,
因此点A′′与点A′重合,
那么A′′C′′与A′C′重合,
因此△A′′B′′C′′ ≌△A′B′C′,
从而△ABC ≌△A′B′C′.
A
B
C
利用“SAS”判定三角形全等
新知探究
(2)△ABC和△A′B′C′的位置关系如图(顶点B 与顶点B′重合).
因为BC=B′C′,
将△ABC作绕点B的旋转,旋转角等于∠C′BC,
所以线段BC的像与线段B′C′重合.
因为∠ABC=∠A′B′C′,
所以∠C′BC=∠A′BA.
(A)
B
(C)
利用“SAS”判定三角形全等
新知探究
由于旋转不改变图形的形状和大小,
又因为BA=B′A′,
所以在上述旋转下,BA的像与B′A重合,
从而AC的像就与A′C′ 重合,
于是△ABC的像就是△A′B′C′ .
因此△ABC ≌△A′B′C′.
(A)
B
(C)
利用“SAS”判定三角形全等
新知探究
(3)△ABC和△A′B′C′的位置关系如图.
根据情形(1)(2)的结论得△A′′B′′C′′ ≌△A′B′C′.
将△ABC作平移,使顶点B的像B′′和顶点B′重合,
因此△ABC ≌△A′B′C′.
利用“SAS”判定三角形全等
新知探究
(4)△ABC 和△A′B′C′的位置关系如图.
将△ABC作关于直线BC的轴反射,
△ABC在轴反射下的像为△A′′BC.
由于轴反射不改变图形的形状和大小,
得△ABC≌△A′′BC.
根据情形(3)的结论得△A′′BC≌△A′B′C′.
因此△ABC ≌△A′B′C′.
利用“SAS”判定三角形全等
新知探究
小归纳
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
文字语言:两边和它们的夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS ”).
“边角边”判定方法
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
新知探究
如图,在△ABC和 △A′B′C′中,如果BC =B′C′,∠B=∠B′,∠C=∠C′,你能通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合吗?那么△ABC与△A′B′C′全等吗?
C'
A'
B'
B
A
C
利用“ASA”判定三角形全等
新知探究
类似于基本事实“SAS”的探究,同样地,我们可以通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合,因此△ABC ≌△A′B′C′.
利用“ASA”判定三角形全等
新知探究
“角边角”判定方法
文字语言:两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
利用“ASA”判定三角形全等
新知探究
利用“AAS”判定三角形全等
若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
60°
45°
新知探究
△ABC≌△A'B'C'.根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件.
在△ABC和 中,
∵ ∠A = ∠A′,∠B = ∠B′,
∴ ∠C =∠C′.
又∵ ,∠B=∠B′,
∴ (ASA).
利用“AAS”判定三角形全等
新知探究
归纳总结
两角分别相等且其中一组等角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
∴ △ABC≌△ A′ B′ C′ (AAS).
A
B
C
A ′
B ′
C ′
新知探究
利用“SSS”判定三角形全等
如图,在△ABC和△A′B′C′中,如果AB=A′B′,BC
= B′C′,AC= A′C′ ,那么△ABC与△A′B′C′全等吗?
如果能够说明∠A=∠A′,那么就可以由“边角边”得出△ABC≌△A′B′C′.
新知探究
由上述变换性质可知△ABC ≌ ,
则 ,
连接
将△ABC作平移、旋转和轴反射等变换,使BC的像 与 重合,并使点A的像 与点 在 的两旁,△ABC在上述变换下的像为
利用“SSS”判定三角形全等
新知探究
∴ ∠1=∠2,∠3=∠4.
从而∠1+∠3=∠2+∠4,
∵ , ,
即
在 和 中,
∴ ≌ (SAS).
∴ △ABC ≌
,
,
,
利用“SSS”判定三角形全等
新知探究
归纳总结
文字语言:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
“边边边”判定方法
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
几何语言:
新知探究
练一练
已知:如图,在△ABC中,AB=AC,点D,E
在BC上,且AD=AE,BE=CD.
求证:△ABD≌△ACE.
证明 ∵ BE = CD,
∴ BE-DE = CD-DE.
即 BD = CE.
在△ABD和△ACE中,
∴ △ABD≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
新知探究
三角形的稳定性
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
新知探究
练一练
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
下列图形中哪些具有稳定性.
03 典型例题
典型例题
1.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴ ∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,
即 AF=CE.
(已知),
(已证),
(已证),
典型例题
2. 已知:如图,△ABC≌△A′B′C′,CF,C′F′分别是∠ACB和∠A′C′B′的平分线. 求证:CF=C′F′.
证明:∵△ABC≌△A′B′C′,
∠A =∠A′ ,
∠ACB =∠A′C′B′.
∴ AC=A′C′,
∴ CF=C′F′.
又∵CF,C′F′分别是∠ACB和∠A′C′B′的平分线,
∴ ∠ACF=∠A′C′F′.
∴ △ACF≌△A′C′F′
典型例题
3. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:BD=CE.
证明: ∵BD⊥AC,CE⊥AB,
∵ 在△CDB和△BEC中,
∠ACB=∠ABC,
BC = BC ,
∴ △CDB≌△BEC(AAS).
∠CDB=∠BEC =90°,
∴ BD = CE.
∴ ∠CDB=∠BEC =90°.
典型例题
4.已知:如图 ,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)∵ AD=FB,
∴AB=FD(等式性质).
在△ABC和△FDE 中,
AC=FE(已知),
BC=DE(已知),
AB=FD(已证),
∴△ABC≌△FDE(SSS);
A
C
E
D
B
F
=
=
?
?
。
。
(2) ∵ △ABC≌△FDE(已证).
∴ ∠C=∠E(全等三角形的对应角相等).
典型例题
5.如图,AC=BD,∠CAB= ∠DBA,求证:BC=AD.
A
B
C
D
证明:在△ABC与△BAD中
AC=BD,
∠CAB=∠DBA,
AB=BA,
∴△ABC≌△BAD(SAS),
(已知)
(已知)
(公共边)
∴BC=AD
(全等三角形的对应边相等).
04 拓展提高
拓展提高
1.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
拓展提高
2.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
拓展提高
3.如图,已知AB=AE,∠1=∠2,∠B=∠E, 求证:BC=ED.
证明:∵∠1=∠2,
∴ ∠1+∠BAD=∠2+∠BAD,
即∠EAD=∠BAC.
在△AED和△ABC中,
∠E=∠B,
AE=AB,
∠EAD=∠BAC,
∴△AED≌△ABC(ASA),
∴BC=ED.
∵
A
B
E
C
D
1
2
拓展提高
4.小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流.
E
F
D
H
解:能.在△EDH和△FDH中 ,
ED=FD,(已知)
∠EDH=∠FDH,(已知)
DH=DH,(公共边)
∴△EDH≌△FDH(SAS),
∴EH=FH.(全等三角形对应边相等)
05 课堂小结
课堂小结
判定三角形全等的思路
已知两边
已知一边一角
已知两角
找夹角(SAS)
找另一边(SSS)
找任一角(AAS)
边为角的对边
边为角的一边
找夹角的另一边(SAS)
找边的对角(AAS)
找夹角的另一角(ASA)
找夹边(ASA)
找除夹边外的任意一边(AAS)
06 作业布置
完成课本习题 2.5 A、B组
作业布置
谢 谢 观 看
同课章节目录
