湘教版八年级数学上册第3章实数3.1 平方根教学课件(共43张)
文档属性
| 名称 | 湘教版八年级数学上册第3章实数3.1 平方根教学课件(共43张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-12 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
平方根
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
为了美化校园,学校打算建一个面积为225平方米的正方形植物园,这个正方形的边长应取多少?你能计算出来吗?
?
解析:根据正方形的面积公式
即:边长
由于
因此正方形的边长应取15m
同学们是如何想到这种通过面积得到边长的方法的呢?接下来让我们来仔细研究这种反向的方法吧!
02 新知探究
新知探究
平方根
想一想 如果一个数的平方等于9,这个数是多少?
由于 ,
所以这个数是3或-3.
3和-3互为相反数,会不会是巧合呢
新知探究
平方根
根据上述问题,即要找出一个数,使它的平方等于给定的数.由此我们抽象出下述概念:
如果有一个数r,使得r2=a,那么我们把r叫作a的一个平方根,也叫作二次方根.
若r2=a,则r是a的一个平方根.
新知探究
想一想
除了2和-2以外,4的平方根还有其他的数吗?
因为边长大于2的正方形,它的面积一定大于4,所以,比2大的数都不是4的平方根.
类似地,边长小于2的正方形,它的面积一定小于4,因此,比2小的正数都不是4的平方根.
边长为2
边长为4
<
新知探究
小归纳
若 r 是正数 a 的一个平方根,那么a的平方根有且只有两个:r与-r.
我们把正数a的正平方根记作 ,读作“根号a”;
把a的负平方根记作 ,读作“负根号a”.
正数a的平方根可以用 “ ”来表示.
新知探究
想一想
零的平方根是多少?负数有平方根吗?
由于02=0,而非零数的平方不等于0,因此零的平方根就是0本身.
由于同号两数相乘得正数,且02=0,即在迄今为止我们所认识的数中,任何一个数的平方都不会是负数,因此负数没有平方根.
小结:正数平方根有两个,它们互为相反数;零的平方根是0;负数没有平方根.
新知探究
小归纳
求一个非负数的平方根的运算,叫作开平方.开平方与平方互为逆运算.
+1
-1
+2
-2
+3
-3
1
4
9
开平方
平方
新知探究
无理数的认识
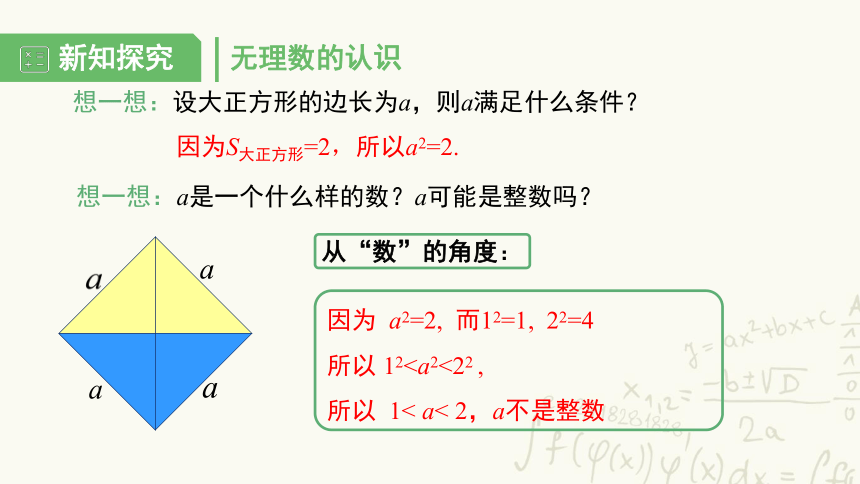
想一想:设大正方形的边长为a,则a满足什么条件?
想一想:a是一个什么样的数?a可能是整数吗?
因为S大正方形=2,所以a2=2.
从“数”的角度:
因为 a2=2, 而12=1, 22=4
所以 12所以 1< a< 2,a不是整数
新知探究
无理数的认识
B
A
C
取出一个三角形
从“形”的角度:
在三角形ABC中,AC=1,BC=1,AB=a
根据三角形的三边关系:
AC-BC< a 所以0
新知探究
无理数的认识
想一想:a可能是分数吗?
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
④ a是分母为多少的分数?
归纳:a既不是整数,也不是分数,所以a不是有理数.
新知探究
无理数的认识
观察下列结果:
2.82=7.84, 2.92=8.41;
2.822=7.9524 2.832=8.0089
2.8282=7.997584 2.8292=8.003241
… …
想一想:a究竟是多少?
新知探究
无理数的认识
从上述数据,你能猜出面积为8的正方形的边长是多少吗?
面积为8的正方形,它的边长应该比2.828大,比2.829小……
既不是有限小数,也不是无限循环小数,这种小数叫作无限不循环小数.把无限不循环小数叫作无理数.
新知探究
练一练
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
新知探究
无理数
我们常见的无理数的有以下三种形式:
(1)含 的一些数,如2 ;
(2)开不尽方的数,如 ;
(3)有规律但不循环的数,如1.010 010 001 000 01…
新知探究
练一练
1.分别求下列各数的平方根:
36, ,1.21.
解 : 由于62=36, 因此36的平方根是6与-6.
即
由于 2= ,
因此 的平方根是 与 .
即
由于1.12=1.21,
因此1.21的平方根是1.1与-1.1.
即
新知探究
练一练
① 的平方根是_______;
② (-16)2的平方根是_______.
2.填一填
新知探究
练一练
3. 设n为正整数,且n< <n+1,则n的值为( )
A.5 B.6 C.7 D.8
解析:根据特殊有理数找出最接近的完全平方数,问题可得到解决.∵ < < ,∴8< <9,∴n=8.
D
方法总结:开不尽的平方根形式的无理数的估算一般步骤是首先将原数平方,看其在哪两个相邻的平方数之间,运用这种方法可以估计一个带根号的数的整数部分,估计其大致范围.
新知探究
算术平方根的概念及其性质
我们把正数a的正平方根 叫作a的算术平方根.
想一想:正数、负数、0的算术平方各有几个?
正数的算术平方根是一个正数,
0的算术平方根还是0,
负数没有算术平方根.
新知探究
算术平方根的概念及其性质
算术平方根的性质:
非负数
非负数
(a≥0)
算术平方根具有双重非负性
新知探究
练一练
4.判断下列说法是否正确.
①25的算术平方根是5 ( );
②25的平方根是5 ( );
③5是25的平方根 ( ).
√
√
注意区分“平方根”与“算术平方根”意义
新知探究
练一练
5.若|m-1| + =0,求m+n的值.
解: 因为|m-1| ≥0, ≥0,
又|m-1| + =0,
所以 |m-1| =0, =0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
方法归纳:几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
新知探究
小归纳
平方根与算术平方根的联系与区别:
1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
1.个数不同:一个正数有两个平方根,但只有一个算术平方根.
2.表示法不同:平方根表示为 ,
而算术平方根表示为 .
联系:
区别:
新知探究
用计算器求算术平方根
想一想:怎么用小数近似地表示一个无理数呢?
例如 …,用四舍五入法,分别取到小数点后面第二位,第三位,…,得到 ,
,…,我们称 3.14,3.142是 的精确到小数点后面第二位,第三位的近似值.
新知探究
练一练
4. 用计算器求下列各式的值.
(1)
解:(1)依次按键:
显示:32
所以,
1
2
0
4
=
新知探究
练一练
(2) (精确到小数点后面第三位).
解:(2)依次按键:
显示:2.828 427 125
所以,
8
=
03 典型例题
例题讲解
1. 分别求 64, ,6.25的平方根.
解
: 64的平方根是8与 -8, 的平方根是 与 ,6.25的平方根是2.5与-2.5.
2. 分别求 81, ,0.16的算术平方根.
解: 81的算术平方根是9, 的算术平方根是 ,0.16的算术平方根是0.4.
例题讲解
3. 判断下列说法是否正确.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
(4)(-4)2的平方根是-4.
正确.
正确.
不正确,是 4.
不正确,是 ±4.
例题讲解
4.下列各数: 1, (相邻两个3之间0的个数逐次加1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
A
【解析】无限不循环小数是无理数,其中
(相邻两个3之间0的个数逐次加1)是无理数,其他是有理数.
例题讲解
5.下列各数中,是无理数的为( )
A. 3.14 B. C. D.
C
【解析】因为3.14是小数, 是分数, 是无限循环小
数,所以选项A,B,D都是有理数; 是无限不循环小数,所以是无理数.
04 拓展提高
拓展提高
1.已知 ,求x的值.
解:∵
∴
∴ x=12 或 x=-10.
拓展提高
2. 面积为6cm2的正方形,它的边长是多少?用计算器求边长的近似值(精确到0.001cm).
正方形的面积是6cm2,因此它的边长为 cm.
解:
用计算器计算 :显示2.4494897,
所以, .
05 课堂小结
课堂小结
平方根的概念
正数的平方根
0的平方根
负数的平方根
正平方根
负平方根
↑
算术平方根
(就是0本身)
→
(没有)
→
课堂小结
→
无理数
带省略号且不循环的小数
有特殊意义的数,如π等
带根号,但被开方数是开方不尽的数
用计算器计算
↓
概念
06 作业布置
完成课本习题 3.1 A、B组
作业布置
谢 谢 观 看
平方根
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
为了美化校园,学校打算建一个面积为225平方米的正方形植物园,这个正方形的边长应取多少?你能计算出来吗?
?
解析:根据正方形的面积公式
即:边长
由于
因此正方形的边长应取15m
同学们是如何想到这种通过面积得到边长的方法的呢?接下来让我们来仔细研究这种反向的方法吧!
02 新知探究
新知探究
平方根
想一想 如果一个数的平方等于9,这个数是多少?
由于 ,
所以这个数是3或-3.
3和-3互为相反数,会不会是巧合呢
新知探究
平方根
根据上述问题,即要找出一个数,使它的平方等于给定的数.由此我们抽象出下述概念:
如果有一个数r,使得r2=a,那么我们把r叫作a的一个平方根,也叫作二次方根.
若r2=a,则r是a的一个平方根.
新知探究
想一想
除了2和-2以外,4的平方根还有其他的数吗?
因为边长大于2的正方形,它的面积一定大于4,所以,比2大的数都不是4的平方根.
类似地,边长小于2的正方形,它的面积一定小于4,因此,比2小的正数都不是4的平方根.
边长为2
边长为4
<
新知探究
小归纳
若 r 是正数 a 的一个平方根,那么a的平方根有且只有两个:r与-r.
我们把正数a的正平方根记作 ,读作“根号a”;
把a的负平方根记作 ,读作“负根号a”.
正数a的平方根可以用 “ ”来表示.
新知探究
想一想
零的平方根是多少?负数有平方根吗?
由于02=0,而非零数的平方不等于0,因此零的平方根就是0本身.
由于同号两数相乘得正数,且02=0,即在迄今为止我们所认识的数中,任何一个数的平方都不会是负数,因此负数没有平方根.
小结:正数平方根有两个,它们互为相反数;零的平方根是0;负数没有平方根.
新知探究
小归纳
求一个非负数的平方根的运算,叫作开平方.开平方与平方互为逆运算.
+1
-1
+2
-2
+3
-3
1
4
9
开平方
平方
新知探究
无理数的认识
想一想:设大正方形的边长为a,则a满足什么条件?
想一想:a是一个什么样的数?a可能是整数吗?
因为S大正方形=2,所以a2=2.
从“数”的角度:
因为 a2=2, 而12=1, 22=4
所以 12
新知探究
无理数的认识
B
A
C
取出一个三角形
从“形”的角度:
在三角形ABC中,AC=1,BC=1,AB=a
根据三角形的三边关系:
AC-BC< a
新知探究
无理数的认识
想一想:a可能是分数吗?
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
④ a是分母为多少的分数?
归纳:a既不是整数,也不是分数,所以a不是有理数.
新知探究
无理数的认识
观察下列结果:
2.82=7.84, 2.92=8.41;
2.822=7.9524 2.832=8.0089
2.8282=7.997584 2.8292=8.003241
… …
想一想:a究竟是多少?
新知探究
无理数的认识
从上述数据,你能猜出面积为8的正方形的边长是多少吗?
面积为8的正方形,它的边长应该比2.828大,比2.829小……
既不是有限小数,也不是无限循环小数,这种小数叫作无限不循环小数.把无限不循环小数叫作无理数.
新知探究
练一练
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
新知探究
无理数
我们常见的无理数的有以下三种形式:
(1)含 的一些数,如2 ;
(2)开不尽方的数,如 ;
(3)有规律但不循环的数,如1.010 010 001 000 01…
新知探究
练一练
1.分别求下列各数的平方根:
36, ,1.21.
解 : 由于62=36, 因此36的平方根是6与-6.
即
由于 2= ,
因此 的平方根是 与 .
即
由于1.12=1.21,
因此1.21的平方根是1.1与-1.1.
即
新知探究
练一练
① 的平方根是_______;
② (-16)2的平方根是_______.
2.填一填
新知探究
练一练
3. 设n为正整数,且n< <n+1,则n的值为( )
A.5 B.6 C.7 D.8
解析:根据特殊有理数找出最接近的完全平方数,问题可得到解决.∵ < < ,∴8< <9,∴n=8.
D
方法总结:开不尽的平方根形式的无理数的估算一般步骤是首先将原数平方,看其在哪两个相邻的平方数之间,运用这种方法可以估计一个带根号的数的整数部分,估计其大致范围.
新知探究
算术平方根的概念及其性质
我们把正数a的正平方根 叫作a的算术平方根.
想一想:正数、负数、0的算术平方各有几个?
正数的算术平方根是一个正数,
0的算术平方根还是0,
负数没有算术平方根.
新知探究
算术平方根的概念及其性质
算术平方根的性质:
非负数
非负数
(a≥0)
算术平方根具有双重非负性
新知探究
练一练
4.判断下列说法是否正确.
①25的算术平方根是5 ( );
②25的平方根是5 ( );
③5是25的平方根 ( ).
√
√
注意区分“平方根”与“算术平方根”意义
新知探究
练一练
5.若|m-1| + =0,求m+n的值.
解: 因为|m-1| ≥0, ≥0,
又|m-1| + =0,
所以 |m-1| =0, =0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
方法归纳:几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
新知探究
小归纳
平方根与算术平方根的联系与区别:
1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
1.个数不同:一个正数有两个平方根,但只有一个算术平方根.
2.表示法不同:平方根表示为 ,
而算术平方根表示为 .
联系:
区别:
新知探究
用计算器求算术平方根
想一想:怎么用小数近似地表示一个无理数呢?
例如 …,用四舍五入法,分别取到小数点后面第二位,第三位,…,得到 ,
,…,我们称 3.14,3.142是 的精确到小数点后面第二位,第三位的近似值.
新知探究
练一练
4. 用计算器求下列各式的值.
(1)
解:(1)依次按键:
显示:32
所以,
1
2
0
4
=
新知探究
练一练
(2) (精确到小数点后面第三位).
解:(2)依次按键:
显示:2.828 427 125
所以,
8
=
03 典型例题
例题讲解
1. 分别求 64, ,6.25的平方根.
解
: 64的平方根是8与 -8, 的平方根是 与 ,6.25的平方根是2.5与-2.5.
2. 分别求 81, ,0.16的算术平方根.
解: 81的算术平方根是9, 的算术平方根是 ,0.16的算术平方根是0.4.
例题讲解
3. 判断下列说法是否正确.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
(4)(-4)2的平方根是-4.
正确.
正确.
不正确,是 4.
不正确,是 ±4.
例题讲解
4.下列各数: 1, (相邻两个3之间0的个数逐次加1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
A
【解析】无限不循环小数是无理数,其中
(相邻两个3之间0的个数逐次加1)是无理数,其他是有理数.
例题讲解
5.下列各数中,是无理数的为( )
A. 3.14 B. C. D.
C
【解析】因为3.14是小数, 是分数, 是无限循环小
数,所以选项A,B,D都是有理数; 是无限不循环小数,所以是无理数.
04 拓展提高
拓展提高
1.已知 ,求x的值.
解:∵
∴
∴ x=12 或 x=-10.
拓展提高
2. 面积为6cm2的正方形,它的边长是多少?用计算器求边长的近似值(精确到0.001cm).
正方形的面积是6cm2,因此它的边长为 cm.
解:
用计算器计算 :显示2.4494897,
所以, .
05 课堂小结
课堂小结
平方根的概念
正数的平方根
0的平方根
负数的平方根
正平方根
负平方根
↑
算术平方根
(就是0本身)
→
(没有)
→
课堂小结
→
无理数
带省略号且不循环的小数
有特殊意义的数,如π等
带根号,但被开方数是开方不尽的数
用计算器计算
↓
概念
06 作业布置
完成课本习题 3.1 A、B组
作业布置
谢 谢 观 看
同课章节目录
