1.2函数概念、表示法限时训练 同步练习(含答案)
文档属性
| 名称 | 1.2函数概念、表示法限时训练 同步练习(含答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
函数概念、表示法限时训练
一.选择题(共16小题,满分80分,每小题5分)
1.已知集合A=R,B={(x,y)|x,y∈R},f:A→B是A到B的映射,f:x→(x+1,x2+1),则以下选项中哪个可能是像( )
A.1 B.2 C.(2,3) D.(3,5)
2.已知函数f(x+1)的定义域为(﹣2,0),则f(2x﹣1)的定义域为( )
A.(﹣1,0) B.() C.(0,1) D.(﹣,0)
3.若函数y=f(x)的值域是[0,3],则函数F(x)=2﹣f(x﹣3),的值域是( )
A.[0,3] B.[1,4] C.[﹣1,2] D.[2,5]
4.若函数y=f(x)的定义域为{x|﹣2≤x≤3,且x≠2},值域为{y|﹣1≤y≤2,且y≠0},
则y=f(x)的图象可能是( )
A. B.
C. D.
5.下列四组函数,表示同一函数的是( )
A.f(x)=,g(x)=x
B.f(x)=x,g(x)=
C.f(x)=,g(x)=?
D.f(x)=x,g(x)=
6.已知函数y=的值域为[0,+∞),求a的取值范围为( )
A.a≥1 B.a>1 C.a≤1 D.a<1
7.已知f(x)满足f(x﹣)=x2+,则f(x+1)的表达式为( )
A.f(x+1)=(x+1)2+
B.f(x+1)=(x﹣)2+
C.f(x+1)=(x+1)2+2
D.f(x+1)=(x+1)2+1
8.若函数f(x)的定义域为[0,4],则函数的定义域为( )
A.[0,1] B.[0,1) C.(0,1) D.[0,1)∪(1,4]
9.函数f(x)=的定义域为R,则实数m的取值范围是( )
A.[0,8] B.[0,8) C.[8,+∞) D.(﹣∞,8)
10.函数的值域是( )
A. B. C. D.
11.函数的图象是( )
A. B.
C. D.
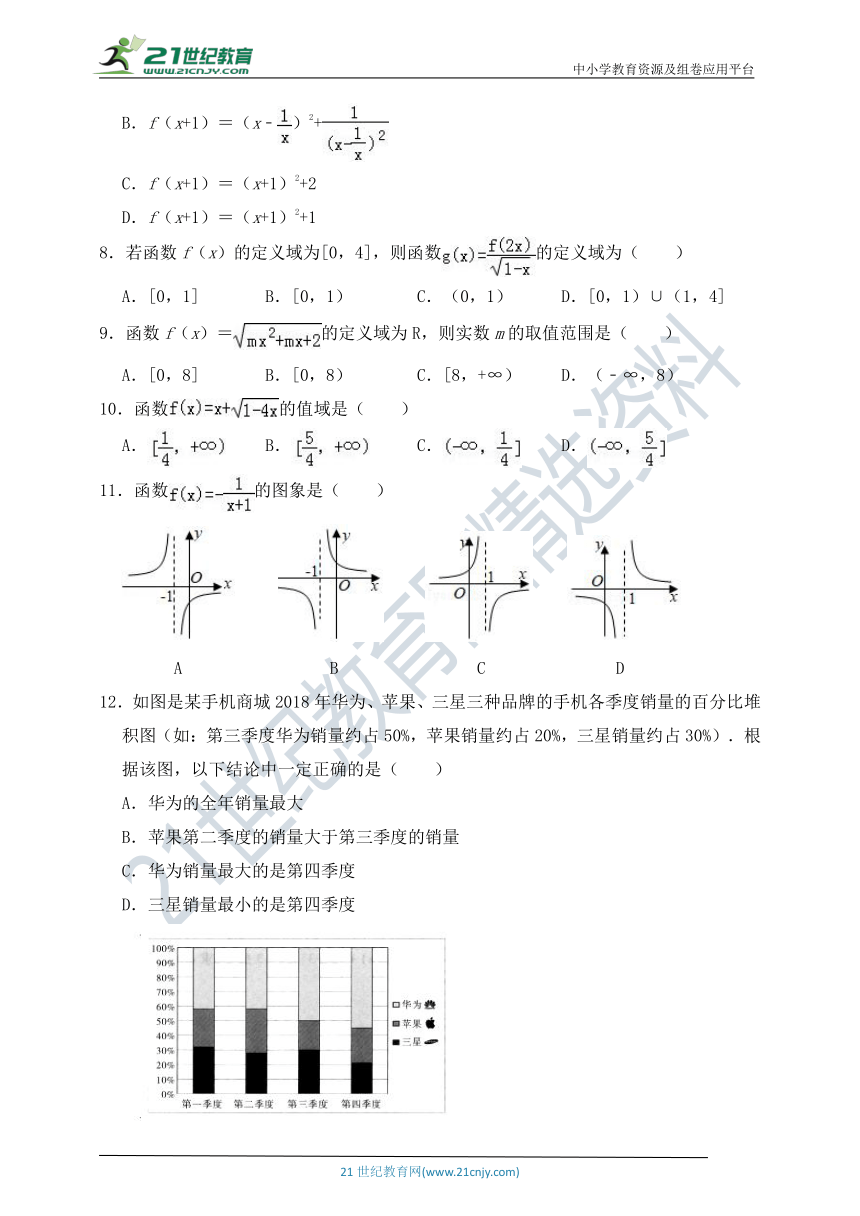
12.如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )
A.华为的全年销量最大
B.苹果第二季度的销量大于第三季度的销量
C.华为销量最大的是第四季度
D.三星销量最小的是第四季度
13.若函数f(x)=(a2﹣2a﹣3)x2+(a+1)x+2的定义域和值域都为R,则a的值为( )
A.3或﹣1 B.3 C.﹣1 D.不确定
14.函数f(x)=的值域是( )
A.R B.(0,2)∪(2,+∞)
C.(0,+∞) D.[0,2]∪[3,+∞)
15.设函数f(x)对x≠0的一切实数均有f(x)+2f()=3x,则f(2018)等于( )
A.2016 B.﹣2016 C.﹣2017 D.2017
16.已知函数f(x)=x2+x+6,存在x∈[0,2],使得f(x)≥a2﹣a成立,则实数a的取值范围( )
A.[﹣3,4] B.[﹣2,3]
C.(﹣∞,﹣2]∪[3,+∞) D.(﹣∞,﹣3]∪[4,+∞)
二.填空题(共2小题,满分10分,每小题5分)
17.下列对应是从集合A到集合B的映射有 .
(1)A=R,B={x|x>0},x∈A,f:x→|x|
(2)A=N,B=N*x∈A,f:x→x2
(3)A={x|x>0},B=R,x∈A,f:x→x2
(4)A=R,B=R,x∈A,f:x→
(5)A={x|1<x<3},B={x|4<x<10},x∈A,f:x→3x+1
18.已知函数f(x)满足,则f(x)的解析式为
函数概念、表示法限训(答案)
一.选择题(共16小题,满分80分,每小题5分)
1.解:根据题意,f:A→B是A到B的映射的像应该为关于x,y的有序数对,故A,B错.
若像为(2,3),则x=1,y应为2,故C错,若像为(3,5),则x=2,y=5.故选:D.
2.解:∵函数f(x+1)的定义域为(﹣2,0),即﹣2<x<0,
∴﹣1<x+1<1,则f(x)的定义域为(﹣1,1),由﹣1<2x﹣1<1,得0<x<1.
∴f(2x﹣1)的定义域为(0,1).故选:C.
3.解:∵y=f(x)的值域是[0,3];∴0≤f(x)≤3;∴0≤f(x﹣3)≤3;
∴﹣1≤2﹣f(x﹣3)≤2;∴F(x)的值域是[﹣1,2].故选:C.
4.解:A.当x=3时,y=0,∴A错误.
B.函数的定义域和值域都满足条件,∴B正确.
C.由函数的图象可知,在图象中出现了有2个函数值y和x对应的图象,∴C错误.
D.函数值域中有两个值不存在,∴函数的值域不满足条件,∴D错误.故选:B.
5.解:A.f(x)==|x|,g(x)=x,所以两个函数的对应法则不一致,所以A不是同一函数.B.f(x)的定义域为R,而g(x)的定义域为(﹣∞,0)∪(0,+∞),所以定义域不同,所以B不是同一函数.C.由x2﹣4≥0,解得x≥2或x≤﹣2,由,解得x≥2,两个函数的定义域不一致,所以C不是同一函数.D.f(x)的定义域为R,而g(x)的定义域为R,且g(x)==x,所以定义域和对应法则相同,所以D是同一函数.故选:D.
6.解:要使函数y=的值域为[0,+∞),则(a﹣1)x2+ax+1能够取到大于0的所有实数.若a﹣1=0,即a=1,函数化为y=,值域为[0,+∞);若a﹣1≠0,则,解得a>1.综上,a的取值范围为a≥1.故选:A.
7.解:f(x)满足f(x﹣)=x2+=(x﹣)2+2,
∴f(x)=x2+2,∴f(x+1)=(x+1)2+2,故选:C.
8.解:∵f(x)的定义域为[0,4];∴g(x)满足:;解得0≤x<1;
∴g(x)的定义域为[0,1).故选:B.
9.解:∵函数f(x)的定义域为R;∴不等式mx2+mx+2≥0的解集为R;
①m=0时,2≥0恒成立,满足题意;②m≠0时,则;
解得0<m≤8;综上得,实数m的取值范围是[0,8].故选:A.
10.解:由1﹣4x≥0得x≤,设t=则t≥0,且t2=1﹣4x,即x=,则f(x)等价为y=+t=﹣(t﹣2)2+,抛物线开口向下,对称轴为t=2,∵t≥0,∴当t=2时函数取得最大值,即f(x)≤,即函数的值域为(﹣∞,],故选:D.
11.解:把y=的图象沿x轴翻折得到y=﹣的图象,再向左平移1个单位得到函数的图象.∴函数的图象是A.故选:A.
12.解:根据图象可看出,华为在每个季度的销量都最大,所以华为的全年销量最大;
∴A正确;每个季度的销量不知道,根据每个季度的百分比是不能比较苹果在第二季度和第三季度销量多少的,同样不能判断华为在哪个季度销量最大,三星在哪个季度销量最小;
∴B,C,D都错误.故选:A.
13.解:∵函数f(x)=(a2﹣2a﹣3)x2+(a+1)x+2的定义域和值域都为R,则,解得a=3.故选:B.
14.解:①当x∈[0,1]时,f(x)=2x2∈[0,2];②当x∈(1,2)时,f(x)=2;③当x∈[2,+∞)时,f(x)=x+1∈[3,+∞)综上所述f(x)的值域为:[0,2]∪[3,+∞)故选:D.
15.解:∵f(x)+2f()=3x①∴f()+2f(x)=②
∴①﹣②×2得﹣3f(x)=3x﹣∴f(x)=﹣x+,
∴f(2018)=﹣2018+2=﹣2016故选:B.
16.解:由题意,可知:函数f(x)=x2+x+6在x∈[0,2]时的值域为y∈[6,12].
∵存在x∈[0,2],使得f(x)≥a2﹣a成立,∴只要使a2﹣a≤12,即可满足题意,
解得﹣3≤a≤4.故选:A.
二.填空题(共2小题,满分10分,每小题5分)
17.解:在(1)中,A=R,B={x|x>0},x∈A,f:x→|x|,
在A中取x<0时,在B中没有元素与之相对应,故(1)不是从集合A到集合B的映射;
在(2)中,A=N,B=N*x∈A,f:x→x2,
在A中取x=0时,在B中没有元素与之相对应,故(2)不是从集合A到集合B的映射;
在(3)中,A={x|x>0},B=R,x∈A,f:x→x2,
在A中任取一个元素x,在B中总有一个唯一的元素与之相对应,
故(2)是从集合A到集合B的映射;
在(4)中,A=R,B=R,x∈A,f:x→不是从集合A到集合B的映射;
在A中取x=0时,在B中没有元素与之相对应,故(4)不是从集合A到集合B的映射;
在(5)中,A={x|1<x<3},B={x|4<x<10},x∈A,f:x→3x+1,
在A中任取一个元素x,在B中总有一个唯一的元素与之相对应,
故(5)是从集合A到集合B的映射.
故答案为:(3)(5).
18.解:在f(x)﹣2f()=2x﹣1 ①中令x=,
得f()﹣2f(x)=﹣1 ②,
由①②联立消去f()得f(x)=﹣x﹣+1,
故答案为:f(x)=﹣x﹣+1.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/8/17 10:20:51;用户:13831894113;邮箱:13831894113;学号:21819650
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
