北师大五年级上册数学教案-第2单元-1:轴对称再认识(一)(含反思+同步习题)
文档属性
| 名称 | 北师大五年级上册数学教案-第2单元-1:轴对称再认识(一)(含反思+同步习题) |  | |
| 格式 | zip | ||
| 文件大小 | 419.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-16 19:49:15 | ||
图片预览




文档简介
1 轴对称再认识(一)
本节课轴对称再认识(一)是属于本册教材第2单元“轴对称和平移”的内容,属于小学数学“空间与图形”领域。教材创设了观察我们经常见到的一些平面图形的情景,引导学生根据情景对前面的知识进行复习,通过折一折的活动,判断哪些平面图形是轴对称图形,哪些不是轴对称图形。
这部分内容是在学生初步认识轴对称图形及对称轴的基础上进行教学的,教材首先呈现了“我们经常见到的平面图形”的主情景,并以此为学习材料,进一步认识轴对称图形及其对称轴。围绕主情景设计了三个问题。第一个问题,判断哪些图形是轴对称图形;第二个问题,讨论平行四边形是否为轴对称图形;第三个问题,寻找轴对称图形的对称轴。加强学生对对称轴概念的理解,突出本节课的重点内容。
1.经历观察、操作等活动,进一步认识轴对称图形及其对称轴。
2.积累图形运动的思维经验,发展空间观念。
3.能根据轴对称图形的特点,在方格纸上画出简单的轴对称图形的对称轴。
4.在探究的过程中,感受到数学在生活中的应用,体会数学的应用价值。
【重点】 理解轴对称图形的特点,会判断一个图形是否是轴对称图形。
【难点】 正确地表示出轴对称图形的对称轴。
【教师准备】 PPT课件,有关本节的图片素材。
【学生准备】 把附页1中的图1剪下来,准备轴对称图形图片若干。
方法一
1.PPT课件展示图片。(天安门、脸谱艺术、剪纸、昆虫图片)
2.引导观察图形,交流汇报。
师:刚才同学们看到的这些图形,在日常生活中还有很多很多,那么,通过观察这些图形,你发现这些图形都有什么特征呢?
预设 生1:两边是一样的。
生2:这些图形是对称的。
师:通过已有的知识,说一说你是怎么理解对称的。
预设 生:对称就是左右两边是完全一样的。
师:同学们,今天我们继续来学习这样的知识——轴对称再认识(一)
(板书课题:轴对称再认识(一))
[设计意图] 通过课件(漂亮的图片)导入新课,吸引学生的注意力,使学生进入学习状态,能起到学生心情愉悦,引起学生情感上的共鸣,更符合学生的年龄特点,更加增强学生学习的兴趣。
方法二
开门见山,直接导入:PPT课件出示教材第21页常见的一些平面图形。
师:(教师边指导学生看大屏幕边说)同学们,你们认识这些平面图形吗?
预设 生:认识。
师:你能说出它们的名字吗?
预设 生:长方形,正方形,平行四边形,梯形……
师:同学们,在这些图形中,有些图形还具有另外的一个特征,就是它们之中有一些图形是轴对称图形,你们能找出来吗?
预设 生:第①,②,④,⑤,⑦,⑧是轴对称图形。
师:同学们,你们是怎么判断的呢?
(学生汇报理由,教师不作评价)
师:我们下面继续学习轴对称图形的知识,学习之后,你们就知道判断轴对称图形的依据了。
(板书课题:轴对称再认识(一))
[设计意图] 通过复习旧知引入新知,有助于学生树立自信心,同时为新知的讲解做好铺垫。
一、明确轴对称图形的意义,认识对称轴。
1.PPT课件出示教材第21页常见的一些平面图形。
师:同学们,请看大屏幕,我们判断一下哪些图形是轴对称图形?
预设 生:第①,②,④,⑤,⑦,⑧是轴对称图形。
师:你们确定自己的判断吗?
预设 生:老师,我们确定我们的判断。
师:那么,我们的判断答案是否正确呢?下面我们通过实践来验证一下。请同学们出示学具(附页1中的平面图形)。
2.折一折,发现特征。
师:同学们,把教材附页1中剪下来的图形动手折一折,看一看哪些图形经过对折后两边的部分能完全重合。
独立活动,边动手操作边汇报。
(引导学生发现不是轴对称图形的原因是无论朝哪个方向对折两边的部分都不会重合,因此普通的梯形、平行四边形都不是轴对称图形)
师:哪些图形经过对折能够完全重合?
预设 生1:长方形经过对折,两边的部分能够完全重合。
生2:正方形经过对折,两边的部分能够完全重合。
生3:等腰梯形经过对折,两边的部分能够完全重合。
生4:菱形和等边三角形经过对折,两边的部分能够完全重合。
生5:图形⑧经过对折,两边的部分能够完全重合。
[设计意图] 引导学生进一步直观地感知轴对称图形两边对称的特征,发展学生几何直观思维。
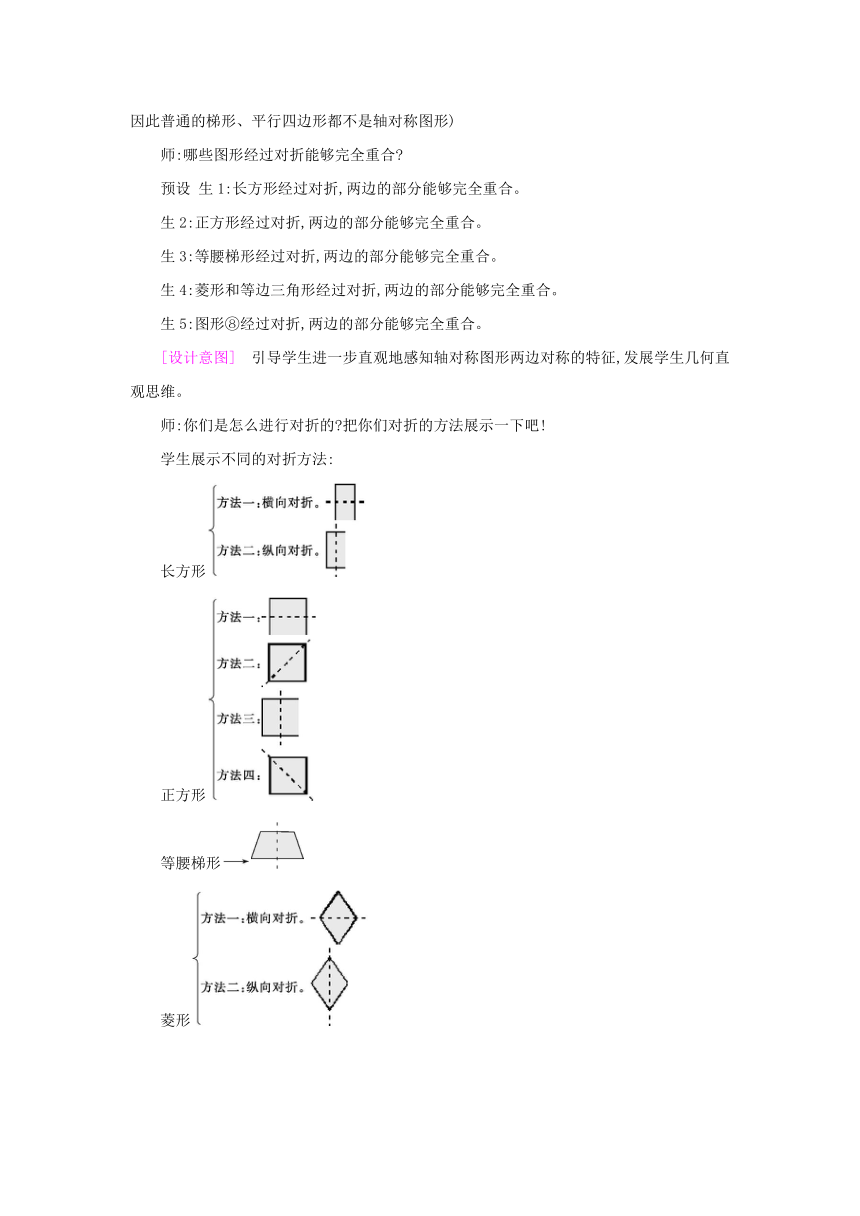
师:你们是怎么进行对折的?把你们对折的方法展示一下吧!
学生展示不同的对折方法:
长方形
正方形
等腰梯形
菱形
等边三角形
图形⑧
师:通过刚才同学们的对折展示,发现了长方形、正方形、等腰梯形……经过对折,两边的图形能够完全重合,这样的图形叫作轴对称图形。
(教师板书:轴对称图形)
师:在折的过程中,每个轴对称图形上都有一条折痕,那么折痕所在的这条直线就是轴对称图形的对称轴。
(教师板书:对称轴)
[设计意图] 引导学生进行操作、探究等活动,使学生有效地认识对称轴的特征,初步感知轴对称图形可能有多条对称轴。
3.总结轴对称图形的意义。
如果一个图形沿着一条直线对折,直线两边的部分能够完全重合,这样的图形叫作轴对称图形。每个轴对称图形上都有一条折痕,那么折痕所在的这条直线就是轴对称图形的对称轴。
二、探究“平行四边形”是否是轴对称图形。
1.PPT课件出示教材第21页第二个问题。
●图③是轴对称图形吗?淘气和笑笑的观点不一样,你同意谁的说法?
师:淘气和笑笑的观点一样吗?
预设 生:淘气和笑笑的观点不一样。
师:他们是怎么说的?(PPT课件出示或者看书)
预设 生1:淘气认为:平行四边形左右两边的图形大小和形状都一样,所以平行四边形是轴对称图形。
生 2:笑笑认为:图③“平行四边形”,无论沿着哪条直线对折,两边的图形都不能够完全重合,所以它不是轴对称图形。
2.小组讨论,回答问题。
师:同学们,你们同意哪个观点?
(学生讨论,小组内交流,然后汇报观点)
预设 生:同意笑笑的观点:平行四边形不是轴对称图形。
师:通过刚才的学习,你们知道轴对称图形有什么特征吗?
预设 生:轴对称图形沿着一条直线对折,两边的部分能够完全重合。
师:我们怎样来判断一个图形是否为轴对称图形呢?
预设 生:我们可以通过折一折的方法,看两边的部分是否能够完全重合,如果能够重合,就是轴对称图形,如果不能重合,就不是轴对称图形。
3.学生动手实践,通过“折一折”验证结论。
师:通过动手实践,你们发现了什么?
(学生汇报,教师同时PPT课件演示,平行四边形多个方向对折的过程)
预设 生1:无论沿着哪条直线对折,直线两边的部分都不能够完全重合。
生2:如果把平行四边形平均分成大小、形状完全相同的两部分,但沿着这条直线对折,平行四边形被这条直线分成形状、大小完全相同的两个部分却不会重合,所以平行四边形不是轴对称图形。
师:同学们说得真好!沿着一条直线对折,直线两边的部分不能够完全重合,就不是轴对称图形,也没有对称轴。
[设计意图] 通过笑笑和淘气截然不同的两个观点,激发学生探究真知的欲望,加深对轴对称图形的理解。
三、学习画对称轴。
1.PPT课件出示教材第21页问题三。
你能找到几条对称轴?画一画,并与同伴说一说。
图形
对称轴条数
1
2.折一折。
师:从我们的学具中找到题目中的平面图形(或者制作题目中的平面图形),从不同的角度进行对折,使折痕两边的图形完全重合,有几条折痕?
(学生动手实践,汇报发现)
学生逐一汇报。
预设 生1:等腰三角形有一条折痕。
生2:长方形有两条折痕。
生3:正方形有四条折痕。
生4:等腰梯形有一条折痕。
生5:菱形有两条折痕。
生6:等边三角形有三条折痕。
生7:最后一个图形有一条折痕。
师:同学们,你们真是爱动手、爱思考的好孩子!通过对折你们都知道每个图形有多少条对称轴了吧!下面我们来完成教材第21页下面的表格。
3.画一画。
(1)明确对称轴的绘画方法。
师:对称轴的画法也很特殊,一般用点画线,也就是用虚线来表示。
(2)画出对称轴,完成表格。
(学生汇报,教师PPT课件演示)
图形
对称轴条数
1
2
4
1
2
3
1
师:通过画对称轴,发现不同的平面图形对称轴的条数也不相同。
4.知识拓展。
师:同学们,圆形有多少条对称轴呢?
(1)学生猜测。
(2)折一折。
师:有多少条对称轴?
预设 生1:折痕很多,说明对称轴很多。
生2:有无数条折痕,所以有无数条对称轴。
总结:圆形有无数条对称轴。
[设计意图] 通过让学生画对称轴,从而知道各种不同的轴对称图形中,对称轴的条数可能是不一样的。
1.完成教材第22页“练一练”的第1题。
2.完成教材第22页“练一练”的第2题。
3.下面图形各有几条对称轴?
4.下面哪些图形是轴对称图形?(是轴对称图形的在括号里打“√”)
5.画出下面图形的对称轴。
【参考答案】 1.前3个(理由略)
2. 3.一条对称轴 一条对称轴 六条对称轴 五条对称轴 4.(√) (√) (√) (√) 5.略
这节课我们一起学习了,如果一个图形沿着一条直线对折,直线两边的部分能够完全重合,这样的图形叫作轴对称图形。每个轴对称图形上折痕所在的直线就是轴对称图形的对称轴。对称轴的画法也很特殊,一般用点画线,也就是用虚线来表示。
作业1
教材第22页“练一练”的第3题。
作业2
【基础巩固】
1.(基础题)我会填。
(1)轴对称图形沿着一条( )对折后,对称轴两边的部分能够完全( ),( )的两部分上的相对应的点到对称轴的距离( )。
(2)画轴对称图形的对称轴,要用( )线画。
(3)轴对称图形至少有( )条对称轴。
2.(重点题)下列图形中,是轴对称图形的有( )。
①线段;②角;③任意三角形;④等腰三角形;⑤等边三角形;⑥直角三角形;⑦等腰直角三角形;⑧圆;⑨长方形;⑩正方形。
【提升培优】
3.(难点题)画出下图中各轴对称图形的对称轴。
4.(易错题)指出下图中的图形是否为轴对称图形,若是,画出它的对称轴。
【思维创新】
5.(创新题)
【参考答案】
作业1:3.提示:引导学生进行想象,先判断是什么样子,而后动手实践。
作业2:1.(1)对称轴 重合 重合 相等 (2)虚 (3)1 2.①②④⑤⑦⑧⑨⑩ 3.略 4.轴对称图形有acef(画对称轴略) 5.略
轴对称再认识(一)
轴对称图形:长方形 正方形 等腰梯形 菱形 等边三角形
不是轴对称图形:平行四边形 普通梯形
对称轴:用虚线画出
在课堂教学中采用了复习导入新知,巩固了学生已有的知识。如:PPT课件呈现常见的平面图形,引领学生进入新知的学习。通过折一折的活动方式,掌握轴对称图形的特点,能够准确地画出轴对称图形的对称轴。
在教学中,学生经历动手实践真知的过程,在这个过程中,放开手脚让学生参与教学活动,充分调动了学生的学习积极性,培养学生的动手能力。
在教学过程中,没有进行深入的拓展,对学生掌握的知识只存在于表面。
在情景创设设计中,设计要注意激发学生的学习兴趣,给学生更大的讨论空间,最大程度调动学生的学习积极性,发挥好学生的主体地位。例如:导入时,可以运用对称美导入教学。
画出下列轴对称图形的对称轴,有几条?
[名师点拨] 通过观察,发现有的轴对称图形只有一条对称轴,有的轴对称图形有多条对称轴。
[解答]
【知识拓展】 由一个平面图形变为另一个平面图形,并使这两个图形关于某一条直线成轴对称,这样的图形变换叫作图形的轴对称变换,也叫作反射变换,简称反射(reflection)。或者是说:如果连接新图形与原图形中每一组对应点的线段都被同一条直线垂直平分,这样的全等变换称为轴对称变换,每组对应点互为对称点,垂直平分对称点所连线段的直线叫作对称轴。
轴对称的重要性
对称在自然界中的存在是一个普遍现象,99%的现代动物是左右对称的,连海葵这种非左右对称动物的后代也存在对称性。
对称性对于人不仅是外在的美,也是健康和生存的需要,如果只有一只眼睛,人们的视野不仅变小,对目标的距离判断不精确,而且对物体的立体形状的认识也会发生扭曲。
人具有独一无二的对称美,所以人们又往往以是否符合“对称性”去审视大自然,并且创造了许多具有对称美的工艺品。
轴对称和轴对称图形的区别
区别:
(1)轴对称是指两个图形间的位置关系,轴对称图形是指一个具有特殊形状的图形;
(2)轴对称涉及两个图形,轴对称图形是对一个图形而言的.
联系:
(1)定义中都有一条直线,都要沿着这条直线折叠重合;
(2)如果把轴对称图形沿对称轴分成两部分(即看成两个图形),那么这两个图形就关于这条直线成轴对称;反过来,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.
本节课轴对称再认识(一)是属于本册教材第2单元“轴对称和平移”的内容,属于小学数学“空间与图形”领域。教材创设了观察我们经常见到的一些平面图形的情景,引导学生根据情景对前面的知识进行复习,通过折一折的活动,判断哪些平面图形是轴对称图形,哪些不是轴对称图形。
这部分内容是在学生初步认识轴对称图形及对称轴的基础上进行教学的,教材首先呈现了“我们经常见到的平面图形”的主情景,并以此为学习材料,进一步认识轴对称图形及其对称轴。围绕主情景设计了三个问题。第一个问题,判断哪些图形是轴对称图形;第二个问题,讨论平行四边形是否为轴对称图形;第三个问题,寻找轴对称图形的对称轴。加强学生对对称轴概念的理解,突出本节课的重点内容。
1.经历观察、操作等活动,进一步认识轴对称图形及其对称轴。
2.积累图形运动的思维经验,发展空间观念。
3.能根据轴对称图形的特点,在方格纸上画出简单的轴对称图形的对称轴。
4.在探究的过程中,感受到数学在生活中的应用,体会数学的应用价值。
【重点】 理解轴对称图形的特点,会判断一个图形是否是轴对称图形。
【难点】 正确地表示出轴对称图形的对称轴。
【教师准备】 PPT课件,有关本节的图片素材。
【学生准备】 把附页1中的图1剪下来,准备轴对称图形图片若干。
方法一
1.PPT课件展示图片。(天安门、脸谱艺术、剪纸、昆虫图片)
2.引导观察图形,交流汇报。
师:刚才同学们看到的这些图形,在日常生活中还有很多很多,那么,通过观察这些图形,你发现这些图形都有什么特征呢?
预设 生1:两边是一样的。
生2:这些图形是对称的。
师:通过已有的知识,说一说你是怎么理解对称的。
预设 生:对称就是左右两边是完全一样的。
师:同学们,今天我们继续来学习这样的知识——轴对称再认识(一)
(板书课题:轴对称再认识(一))
[设计意图] 通过课件(漂亮的图片)导入新课,吸引学生的注意力,使学生进入学习状态,能起到学生心情愉悦,引起学生情感上的共鸣,更符合学生的年龄特点,更加增强学生学习的兴趣。
方法二
开门见山,直接导入:PPT课件出示教材第21页常见的一些平面图形。
师:(教师边指导学生看大屏幕边说)同学们,你们认识这些平面图形吗?
预设 生:认识。
师:你能说出它们的名字吗?
预设 生:长方形,正方形,平行四边形,梯形……
师:同学们,在这些图形中,有些图形还具有另外的一个特征,就是它们之中有一些图形是轴对称图形,你们能找出来吗?
预设 生:第①,②,④,⑤,⑦,⑧是轴对称图形。
师:同学们,你们是怎么判断的呢?
(学生汇报理由,教师不作评价)
师:我们下面继续学习轴对称图形的知识,学习之后,你们就知道判断轴对称图形的依据了。
(板书课题:轴对称再认识(一))
[设计意图] 通过复习旧知引入新知,有助于学生树立自信心,同时为新知的讲解做好铺垫。
一、明确轴对称图形的意义,认识对称轴。
1.PPT课件出示教材第21页常见的一些平面图形。
师:同学们,请看大屏幕,我们判断一下哪些图形是轴对称图形?
预设 生:第①,②,④,⑤,⑦,⑧是轴对称图形。
师:你们确定自己的判断吗?
预设 生:老师,我们确定我们的判断。
师:那么,我们的判断答案是否正确呢?下面我们通过实践来验证一下。请同学们出示学具(附页1中的平面图形)。
2.折一折,发现特征。
师:同学们,把教材附页1中剪下来的图形动手折一折,看一看哪些图形经过对折后两边的部分能完全重合。
独立活动,边动手操作边汇报。
(引导学生发现不是轴对称图形的原因是无论朝哪个方向对折两边的部分都不会重合,因此普通的梯形、平行四边形都不是轴对称图形)
师:哪些图形经过对折能够完全重合?
预设 生1:长方形经过对折,两边的部分能够完全重合。
生2:正方形经过对折,两边的部分能够完全重合。
生3:等腰梯形经过对折,两边的部分能够完全重合。
生4:菱形和等边三角形经过对折,两边的部分能够完全重合。
生5:图形⑧经过对折,两边的部分能够完全重合。
[设计意图] 引导学生进一步直观地感知轴对称图形两边对称的特征,发展学生几何直观思维。
师:你们是怎么进行对折的?把你们对折的方法展示一下吧!
学生展示不同的对折方法:
长方形
正方形
等腰梯形
菱形
等边三角形
图形⑧
师:通过刚才同学们的对折展示,发现了长方形、正方形、等腰梯形……经过对折,两边的图形能够完全重合,这样的图形叫作轴对称图形。
(教师板书:轴对称图形)
师:在折的过程中,每个轴对称图形上都有一条折痕,那么折痕所在的这条直线就是轴对称图形的对称轴。
(教师板书:对称轴)
[设计意图] 引导学生进行操作、探究等活动,使学生有效地认识对称轴的特征,初步感知轴对称图形可能有多条对称轴。
3.总结轴对称图形的意义。
如果一个图形沿着一条直线对折,直线两边的部分能够完全重合,这样的图形叫作轴对称图形。每个轴对称图形上都有一条折痕,那么折痕所在的这条直线就是轴对称图形的对称轴。
二、探究“平行四边形”是否是轴对称图形。
1.PPT课件出示教材第21页第二个问题。
●图③是轴对称图形吗?淘气和笑笑的观点不一样,你同意谁的说法?
师:淘气和笑笑的观点一样吗?
预设 生:淘气和笑笑的观点不一样。
师:他们是怎么说的?(PPT课件出示或者看书)
预设 生1:淘气认为:平行四边形左右两边的图形大小和形状都一样,所以平行四边形是轴对称图形。
生 2:笑笑认为:图③“平行四边形”,无论沿着哪条直线对折,两边的图形都不能够完全重合,所以它不是轴对称图形。
2.小组讨论,回答问题。
师:同学们,你们同意哪个观点?
(学生讨论,小组内交流,然后汇报观点)
预设 生:同意笑笑的观点:平行四边形不是轴对称图形。
师:通过刚才的学习,你们知道轴对称图形有什么特征吗?
预设 生:轴对称图形沿着一条直线对折,两边的部分能够完全重合。
师:我们怎样来判断一个图形是否为轴对称图形呢?
预设 生:我们可以通过折一折的方法,看两边的部分是否能够完全重合,如果能够重合,就是轴对称图形,如果不能重合,就不是轴对称图形。
3.学生动手实践,通过“折一折”验证结论。
师:通过动手实践,你们发现了什么?
(学生汇报,教师同时PPT课件演示,平行四边形多个方向对折的过程)
预设 生1:无论沿着哪条直线对折,直线两边的部分都不能够完全重合。
生2:如果把平行四边形平均分成大小、形状完全相同的两部分,但沿着这条直线对折,平行四边形被这条直线分成形状、大小完全相同的两个部分却不会重合,所以平行四边形不是轴对称图形。
师:同学们说得真好!沿着一条直线对折,直线两边的部分不能够完全重合,就不是轴对称图形,也没有对称轴。
[设计意图] 通过笑笑和淘气截然不同的两个观点,激发学生探究真知的欲望,加深对轴对称图形的理解。
三、学习画对称轴。
1.PPT课件出示教材第21页问题三。
你能找到几条对称轴?画一画,并与同伴说一说。
图形
对称轴条数
1
2.折一折。
师:从我们的学具中找到题目中的平面图形(或者制作题目中的平面图形),从不同的角度进行对折,使折痕两边的图形完全重合,有几条折痕?
(学生动手实践,汇报发现)
学生逐一汇报。
预设 生1:等腰三角形有一条折痕。
生2:长方形有两条折痕。
生3:正方形有四条折痕。
生4:等腰梯形有一条折痕。
生5:菱形有两条折痕。
生6:等边三角形有三条折痕。
生7:最后一个图形有一条折痕。
师:同学们,你们真是爱动手、爱思考的好孩子!通过对折你们都知道每个图形有多少条对称轴了吧!下面我们来完成教材第21页下面的表格。
3.画一画。
(1)明确对称轴的绘画方法。
师:对称轴的画法也很特殊,一般用点画线,也就是用虚线来表示。
(2)画出对称轴,完成表格。
(学生汇报,教师PPT课件演示)
图形
对称轴条数
1
2
4
1
2
3
1
师:通过画对称轴,发现不同的平面图形对称轴的条数也不相同。
4.知识拓展。
师:同学们,圆形有多少条对称轴呢?
(1)学生猜测。
(2)折一折。
师:有多少条对称轴?
预设 生1:折痕很多,说明对称轴很多。
生2:有无数条折痕,所以有无数条对称轴。
总结:圆形有无数条对称轴。
[设计意图] 通过让学生画对称轴,从而知道各种不同的轴对称图形中,对称轴的条数可能是不一样的。
1.完成教材第22页“练一练”的第1题。
2.完成教材第22页“练一练”的第2题。
3.下面图形各有几条对称轴?
4.下面哪些图形是轴对称图形?(是轴对称图形的在括号里打“√”)
5.画出下面图形的对称轴。
【参考答案】 1.前3个(理由略)
2. 3.一条对称轴 一条对称轴 六条对称轴 五条对称轴 4.(√) (√) (√) (√) 5.略
这节课我们一起学习了,如果一个图形沿着一条直线对折,直线两边的部分能够完全重合,这样的图形叫作轴对称图形。每个轴对称图形上折痕所在的直线就是轴对称图形的对称轴。对称轴的画法也很特殊,一般用点画线,也就是用虚线来表示。
作业1
教材第22页“练一练”的第3题。
作业2
【基础巩固】
1.(基础题)我会填。
(1)轴对称图形沿着一条( )对折后,对称轴两边的部分能够完全( ),( )的两部分上的相对应的点到对称轴的距离( )。
(2)画轴对称图形的对称轴,要用( )线画。
(3)轴对称图形至少有( )条对称轴。
2.(重点题)下列图形中,是轴对称图形的有( )。
①线段;②角;③任意三角形;④等腰三角形;⑤等边三角形;⑥直角三角形;⑦等腰直角三角形;⑧圆;⑨长方形;⑩正方形。
【提升培优】
3.(难点题)画出下图中各轴对称图形的对称轴。
4.(易错题)指出下图中的图形是否为轴对称图形,若是,画出它的对称轴。
【思维创新】
5.(创新题)
【参考答案】
作业1:3.提示:引导学生进行想象,先判断是什么样子,而后动手实践。
作业2:1.(1)对称轴 重合 重合 相等 (2)虚 (3)1 2.①②④⑤⑦⑧⑨⑩ 3.略 4.轴对称图形有acef(画对称轴略) 5.略
轴对称再认识(一)
轴对称图形:长方形 正方形 等腰梯形 菱形 等边三角形
不是轴对称图形:平行四边形 普通梯形
对称轴:用虚线画出
在课堂教学中采用了复习导入新知,巩固了学生已有的知识。如:PPT课件呈现常见的平面图形,引领学生进入新知的学习。通过折一折的活动方式,掌握轴对称图形的特点,能够准确地画出轴对称图形的对称轴。
在教学中,学生经历动手实践真知的过程,在这个过程中,放开手脚让学生参与教学活动,充分调动了学生的学习积极性,培养学生的动手能力。
在教学过程中,没有进行深入的拓展,对学生掌握的知识只存在于表面。
在情景创设设计中,设计要注意激发学生的学习兴趣,给学生更大的讨论空间,最大程度调动学生的学习积极性,发挥好学生的主体地位。例如:导入时,可以运用对称美导入教学。
画出下列轴对称图形的对称轴,有几条?
[名师点拨] 通过观察,发现有的轴对称图形只有一条对称轴,有的轴对称图形有多条对称轴。
[解答]
【知识拓展】 由一个平面图形变为另一个平面图形,并使这两个图形关于某一条直线成轴对称,这样的图形变换叫作图形的轴对称变换,也叫作反射变换,简称反射(reflection)。或者是说:如果连接新图形与原图形中每一组对应点的线段都被同一条直线垂直平分,这样的全等变换称为轴对称变换,每组对应点互为对称点,垂直平分对称点所连线段的直线叫作对称轴。
轴对称的重要性
对称在自然界中的存在是一个普遍现象,99%的现代动物是左右对称的,连海葵这种非左右对称动物的后代也存在对称性。
对称性对于人不仅是外在的美,也是健康和生存的需要,如果只有一只眼睛,人们的视野不仅变小,对目标的距离判断不精确,而且对物体的立体形状的认识也会发生扭曲。
人具有独一无二的对称美,所以人们又往往以是否符合“对称性”去审视大自然,并且创造了许多具有对称美的工艺品。
轴对称和轴对称图形的区别
区别:
(1)轴对称是指两个图形间的位置关系,轴对称图形是指一个具有特殊形状的图形;
(2)轴对称涉及两个图形,轴对称图形是对一个图形而言的.
联系:
(1)定义中都有一条直线,都要沿着这条直线折叠重合;
(2)如果把轴对称图形沿对称轴分成两部分(即看成两个图形),那么这两个图形就关于这条直线成轴对称;反过来,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
