人教版选修3-1 6.1分析的化身──欧拉课件(25张)
文档属性
| 名称 | 人教版选修3-1 6.1分析的化身──欧拉课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-14 22:14:56 | ||
图片预览



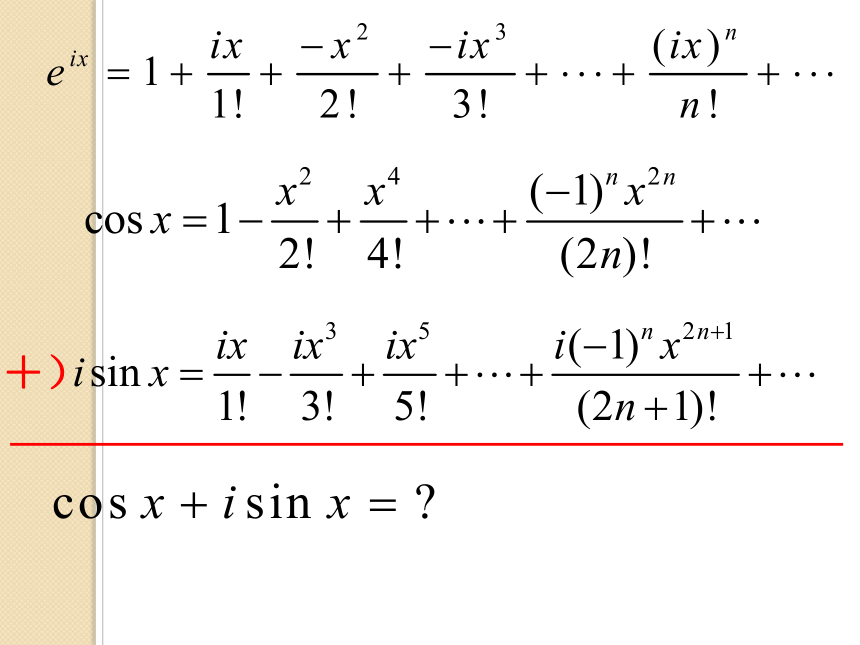
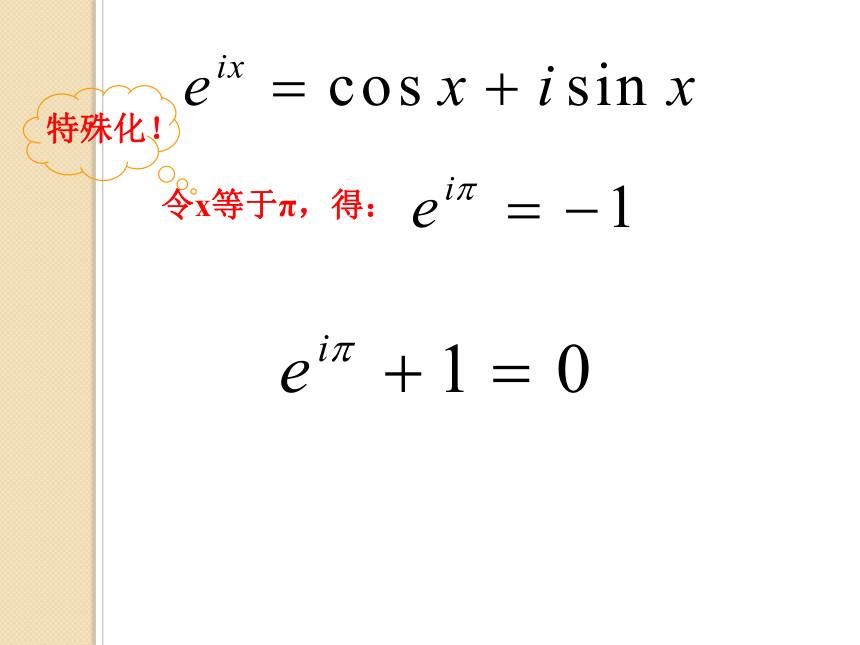

文档简介
课件25张PPT。分析的化身——欧拉1707年欧拉生于瑞士巴塞尔莱昂哈德·欧拉
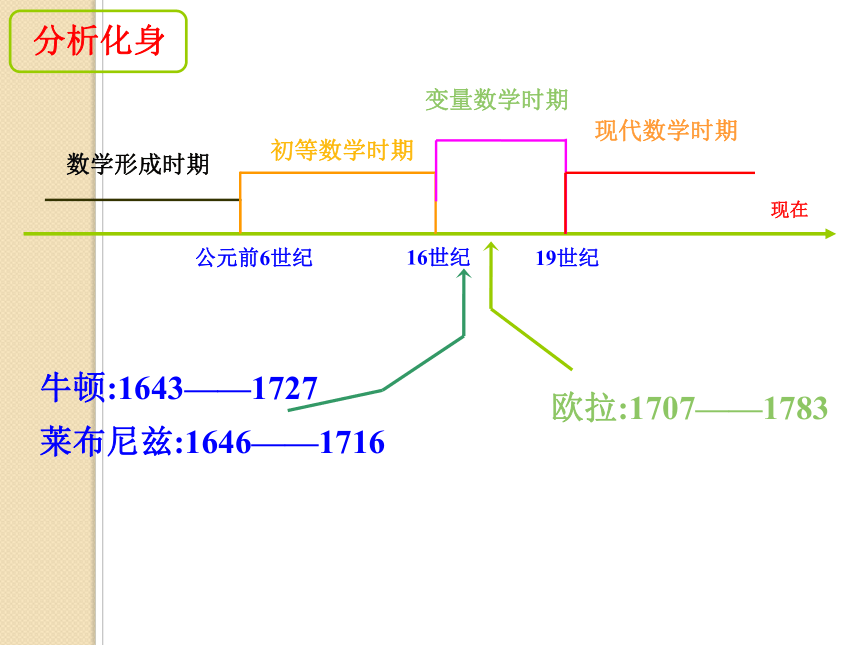
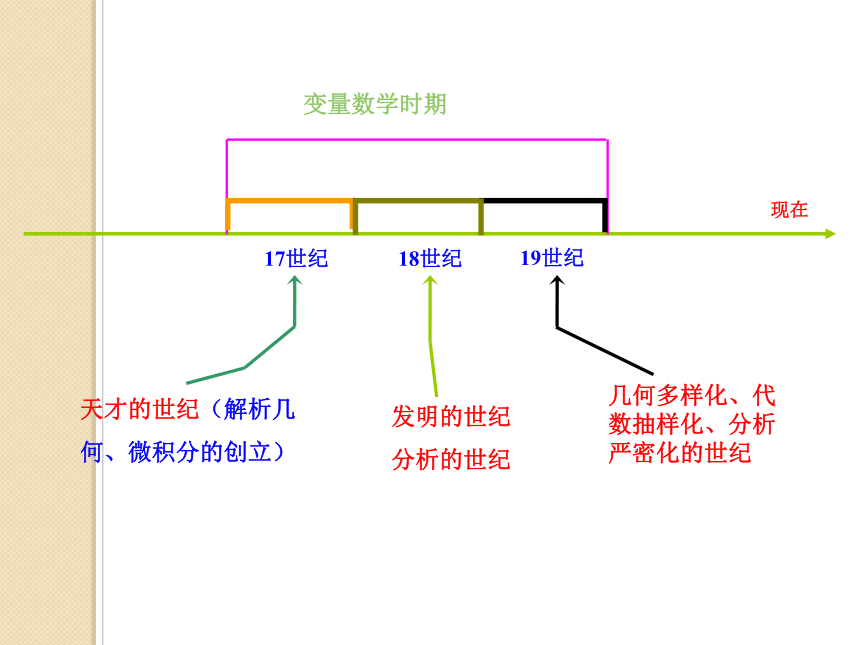
(Leonhard Euler) 1720年(13岁)入读巴塞尔大学,师从微积分权威约翰·伯努利1722年(15岁)大学毕业,获得学士学位1723年(16岁)获得巴赛尔大学的哲学硕士学位 1726年(19岁)受聘于圣彼得堡科学院(工作14年) 1741年受聘于柏林科学院 1766年携家人回到阔别25年的俄国 1771年双目失明,住所发生火灾,财产、手稿付之一炬 1773年前妻去世 1738年积劳成疾,右眼失明 1783年逝于俄国 变量数学时期现在令x等于π,得:f (0)=0从这个意义上说我们的思想与大数学家欧拉是相通的!令x等于0,可得:令x等于π,得:历史上的函数概念约翰·伯努利(1718):
一个变量的函数是由该变量
和一些常数以任何方式组成
的量.Johann Bernoulli, 1667-1748历史上的函数概念欧拉(1748):
一个变量的函数是由该变量
和一些数或常量以任何方式
组成的解析式.
Leonhard Euler, 1707 - 1783历史上的函数概念欧拉(1755):
如果某些量依赖于另一些量,
当后面这些量变化时,前面
这些变量也随之变化,则前
面的量称为后面的量的函数.Leonhard Euler, 1707 - 1783函数概念的发展运动变化过程中的不变性18世纪可成为欧拉的世纪请阅读教材,并回答为什么称巨星欧拉为数学英雄?百折不挠 当然,欧拉也是人,不是神,也并非万能的和永远正确的,他在无穷级数的敛散性上曾出现过错误;他曾研究过“哥德巴赫猜想”而未获得结果.但他亲自把“哥德巴赫猜想”公布于众,并声明自己无法证明,才使之成为世界著名难题,成为数学“皇冠上的明珠”.这些例子,也表明他的高贵品质.1.通过本节课的学习,你对欧拉有多少了解?2.通过对欧拉的了解,你认为可以从欧拉身上学到些什么?欧拉——数学之神
(Leonhard Euler) 1720年(13岁)入读巴塞尔大学,师从微积分权威约翰·伯努利1722年(15岁)大学毕业,获得学士学位1723年(16岁)获得巴赛尔大学的哲学硕士学位 1726年(19岁)受聘于圣彼得堡科学院(工作14年) 1741年受聘于柏林科学院 1766年携家人回到阔别25年的俄国 1771年双目失明,住所发生火灾,财产、手稿付之一炬 1773年前妻去世 1738年积劳成疾,右眼失明 1783年逝于俄国 变量数学时期现在令x等于π,得:f (0)=0从这个意义上说我们的思想与大数学家欧拉是相通的!令x等于0,可得:令x等于π,得:历史上的函数概念约翰·伯努利(1718):
一个变量的函数是由该变量
和一些常数以任何方式组成
的量.Johann Bernoulli, 1667-1748历史上的函数概念欧拉(1748):
一个变量的函数是由该变量
和一些数或常量以任何方式
组成的解析式.
Leonhard Euler, 1707 - 1783历史上的函数概念欧拉(1755):
如果某些量依赖于另一些量,
当后面这些量变化时,前面
这些变量也随之变化,则前
面的量称为后面的量的函数.Leonhard Euler, 1707 - 1783函数概念的发展运动变化过程中的不变性18世纪可成为欧拉的世纪请阅读教材,并回答为什么称巨星欧拉为数学英雄?百折不挠 当然,欧拉也是人,不是神,也并非万能的和永远正确的,他在无穷级数的敛散性上曾出现过错误;他曾研究过“哥德巴赫猜想”而未获得结果.但他亲自把“哥德巴赫猜想”公布于众,并声明自己无法证明,才使之成为世界著名难题,成为数学“皇冠上的明珠”.这些例子,也表明他的高贵品质.1.通过本节课的学习,你对欧拉有多少了解?2.通过对欧拉的了解,你认为可以从欧拉身上学到些什么?欧拉——数学之神
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
