人教版选修4-1 1.2平行线分线段成比例定理课件(18张)
文档属性
| 名称 | 人教版选修4-1 1.2平行线分线段成比例定理课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-14 22:21:44 | ||
图片预览




文档简介
课件18张PPT。平行线分线段成比例定理平行线等分线段定理复习推论1推论2平行线等分线段定理的应用把线段n等分
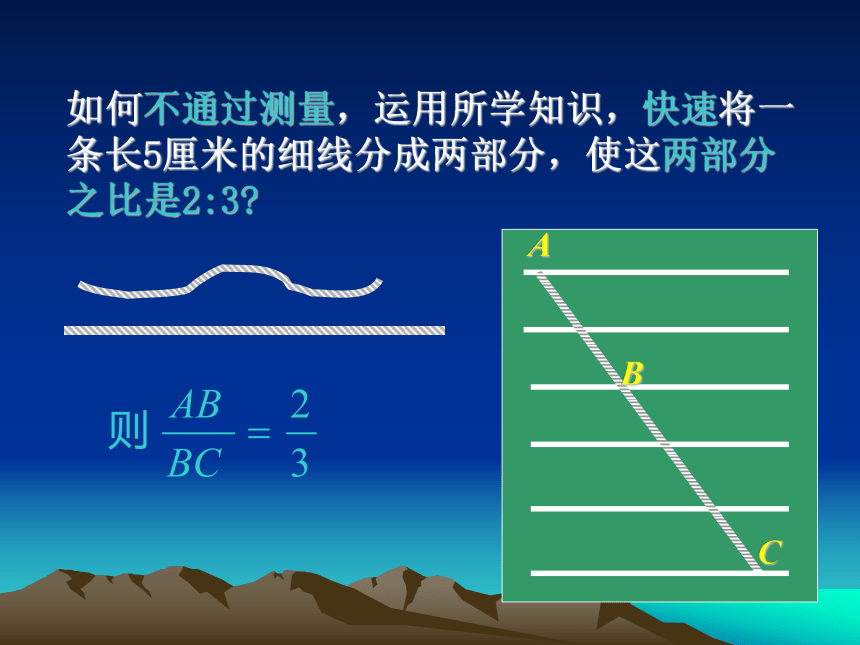
证明同一直线上的线段相等如何不通过测量,运用所学知识,快速将一条长5厘米的细线分成两部分,使这两部分之比是2:3?ABC平行线等分线段定理的条件相邻的两条平行线间的距离相等一组平行线中相邻两条平行
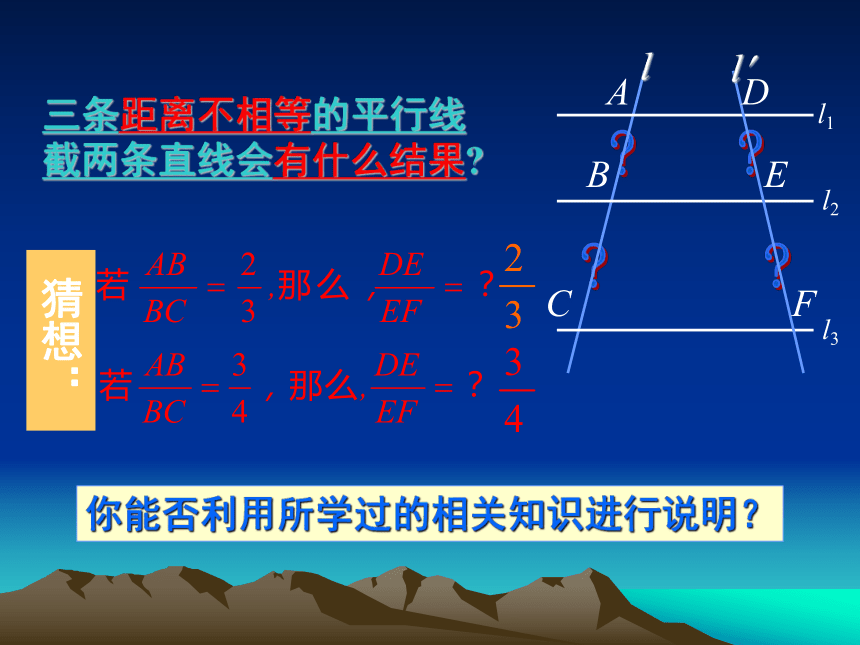
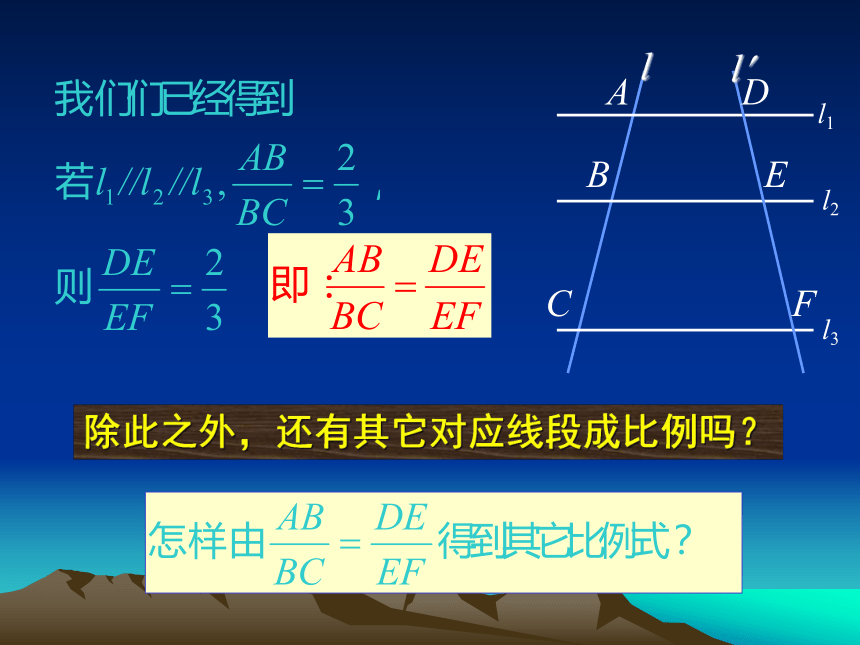
线间距离不相等,结论如何?三条距离不相等的平行线截两条直线会有什么结果?猜想:你能否利用所学过的相关知识进行说明?设线段AB的中点为P1,线段BC的三等分点为P2、P3.则:这时你想到了什么?AP1=P1B=BP2= P2P3= P3CDQ1=Q1E=EQ2=Q2Q3=Q3F平行线等分线段定理分别过点P1,P2, P3作直线a1,a2,a3平行于l1,与l? 的交点分别为Q1,Q2,Q3.ll? 除此之外,还有其它对应线段成比例吗??反 比合 比合 比反 比合比平行线等分线段成比例定理三条平行线截两条直线,所得的对应线段成比例.推论平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.平行线分线段成比例定理与平行线等分线段定理有何联系?结论:后者是前者的一种特殊情况!例 如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2, BC=8.求BF和CF的长.分析:运用平行线分线段成比例定理的推论分别列出比例式求解.解∵DE//BC∵DF//ACDE例 如图,△ABC中,DE//BC,EF//CD.
求证:AD是AB和AF的比例中项.分析: 分别在△ABC及△ADC中利用平行线分线段成比例定理的推论证明∴AD2=AB?AF,即AD是AB和AF的比例中项如图,有一块形状为直角梯形的草地,周围均为水泥直道,两个拐角A、B处均为直角,草地中间另有一条水泥直道EF垂直于AB,垂足为E.已知AE长a米,EB长b米,DF长c米.求CF.用平行于三角形一边且和其他两边相交的直线截三角形,所截得的三角形的三边与原三角形的三边对应成比例.已知:如图,DE//BC,DE分别交AB、AC于点D、EDE=BF 如图,直线l1,l2被三个平行平面?,?,?所截,直线l1与它们的交点分别为A,B,C,直线l2分别为D,E,F探究一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. (关键要能熟练地找出对应线段)小结二、要熟悉该定理的几种基本图形三、注意该定理在三角形中的应用
证明同一直线上的线段相等如何不通过测量,运用所学知识,快速将一条长5厘米的细线分成两部分,使这两部分之比是2:3?ABC平行线等分线段定理的条件相邻的两条平行线间的距离相等一组平行线中相邻两条平行
线间距离不相等,结论如何?三条距离不相等的平行线截两条直线会有什么结果?猜想:你能否利用所学过的相关知识进行说明?设线段AB的中点为P1,线段BC的三等分点为P2、P3.则:这时你想到了什么?AP1=P1B=BP2= P2P3= P3CDQ1=Q1E=EQ2=Q2Q3=Q3F平行线等分线段定理分别过点P1,P2, P3作直线a1,a2,a3平行于l1,与l? 的交点分别为Q1,Q2,Q3.ll? 除此之外,还有其它对应线段成比例吗??反 比合 比合 比反 比合比平行线等分线段成比例定理三条平行线截两条直线,所得的对应线段成比例.推论平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.平行线分线段成比例定理与平行线等分线段定理有何联系?结论:后者是前者的一种特殊情况!例 如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2, BC=8.求BF和CF的长.分析:运用平行线分线段成比例定理的推论分别列出比例式求解.解∵DE//BC∵DF//ACDE例 如图,△ABC中,DE//BC,EF//CD.
求证:AD是AB和AF的比例中项.分析: 分别在△ABC及△ADC中利用平行线分线段成比例定理的推论证明∴AD2=AB?AF,即AD是AB和AF的比例中项如图,有一块形状为直角梯形的草地,周围均为水泥直道,两个拐角A、B处均为直角,草地中间另有一条水泥直道EF垂直于AB,垂足为E.已知AE长a米,EB长b米,DF长c米.求CF.用平行于三角形一边且和其他两边相交的直线截三角形,所截得的三角形的三边与原三角形的三边对应成比例.已知:如图,DE//BC,DE分别交AB、AC于点D、EDE=BF 如图,直线l1,l2被三个平行平面?,?,?所截,直线l1与它们的交点分别为A,B,C,直线l2分别为D,E,F探究一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. (关键要能熟练地找出对应线段)小结二、要熟悉该定理的几种基本图形三、注意该定理在三角形中的应用
