人教版选修1-4 1.4直角三角形的射影定理课件(67张)
文档属性
| 名称 | 人教版选修1-4 1.4直角三角形的射影定理课件(67张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-14 00:00:00 | ||
图片预览











文档简介
课件67张PPT。第一讲——相似三角形的判定及有关性质四 直角三角形的射影定理[学习目标]
1.理解直角三角形的射影定理.
2.理解直角三角形射影定理的逆定理.
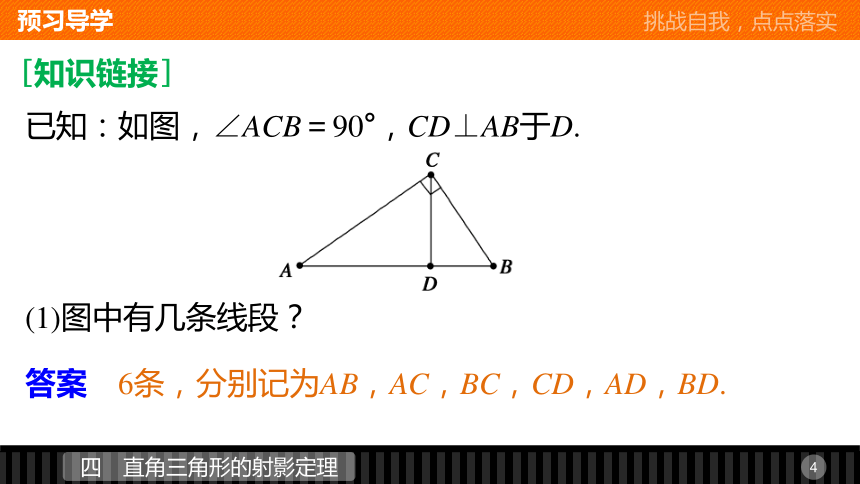
3.能应用直角三角形的射影定理及其逆定理解决相关的几何问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功4分层训练 解疑纠偏,训练检测[知识链接]已知:如图,∠ACB=90°,CD⊥AB于D. (1)图中有几条线段? 答案 6条,分别记为AB,AC,BC,CD,AD,BD. (2)图中有几对相似三角形?可写出几组比例式?
答案 由图中△ACD∽△CBD∽△ABC,可分别写出三组比例式:(3)有几个带有比例中项的比例式?由上可得到哪些等积式?
答案 只有三个比例中项的表达式:可得到等积式:CD2=AD·BD,BC2=BD·BA,AC2=AD·AB .[预习导引]1.射影的有关概念
(1)点在直线上的正射影:从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的 .
(2)线段在直线上的正射影:一条线段在直线上的正射影,是指线段的两个端点在这条直线上的正射影间的线段.正射影2.直角三角形的射影定理
(1)直角三角形的射影定理:直角三角形斜边上的高是两直角边在斜边上射影的 ;两直角边分别是它们在斜边上射影与斜边的 .
(2)符号表示:如图,CD是Rt△ABC的斜边AB
上的高,则AC2= ;BC2= ;CD2
= .比例中项比例中项AD·ABBD·BAAD·BD要点一 用射影定理求线段的长例1 如图,圆O上一点C在直径AB上的射影为D,AD=2,DB=8,求CD,AC和BC的长.解 ∵∠ACB是半圆上的圆周角,∴∠ACB=90°,
即△ABC是直角三角形.
由射影定理可得
CD2=AD·BD=2×8=16,解得CD=4,规律方法 应用射影定理有两个条件:一是直角三角形;二是斜边上的高.在求直角三角形的边长时,根据已知的条件,可以应用射影定理,有时也可应用勾股定理.跟踪演练1 在△ABC中,AC⊥BC,CD⊥AB于点D,若AD=27,BD=3,则AC=__________,BC=__________,
CD=________.
解析 由射影定理,得CD2=AD·BD,则CD=9.
根据勾股定理,得9要点二 用射影定理证明等式例2 如图所示,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DF⊥AC于F,DE⊥AB于E.试证明:(1)AB·AC=AD·BC;证明 在Rt△ABC中,AD⊥BC,∴AB·AC=BC·AD.(2)AD3=BC·BE·CF.
证明 在Rt△ADB中,DE⊥AB,
由射影定理得BD2=BE·AB.
同理CD2=CF·AC,
∴BD2·CD2=BE·AB·CF·AC. ①
又在Rt△BAC中,AD⊥BC,
∴AD2=BD·DC, ②∴由①②两式得AD4=BE·CF·AB·AC,由(1)知AB·AC=BC·AD代入上式得AD3=BE·CF·BC.规律方法 利用直角三角形的射影定理证明恒等式
(1)结合图形,仔细分析题目的结论;
(2)由于射影定理中可供选择的等式较多,需要合理选择.跟踪演练2 如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F.求证:AE·AB=AF·AC.证明 因为AD⊥BC,所以△ADB与△ADC都是直角三角形.
在Rt△ADB中,由于DE⊥AB于E,
所以AD2=AB·AE;
在Rt△ADC中,由于DF⊥AC于F,
所以AD2=AF·AC,
所以AE·AB=AF·AC.要点三 射影定理的综合应用例3 如图所示,在△ABC中,D、F分别在AC、BC上,且AB⊥AC,AF⊥BC,BD=DC=FC=1,求AC.解 在△ABC中,设AC为x,
∵AB⊥AC,AF⊥BC,又FC=1,
根据射影定理,得AC2=FC·BC,即BC=x2.
再由射影定理,得AF2=BF·FC=(BC-FC)·FC,在△BDC中,过D作DE⊥BC于E,
∵BD=DC=1,∴BE=EC,在Rt△DEC中,∵DE2+EC2=DC2,规律方法 (1)由射影定理可得三角形相似,可求相似比、三角形边长等.
(2)射影定理中有三个等式,根据题目需要恰当地进行选择.跟踪演练3 在△ABC中,∠ACB=90°,CD⊥AB于D,AD∶BD=2∶3,则△ACD与△CBD的相似比为( )
A.2∶3 B.4∶9
C. ∶3 D.不确定解析 如题图,在Rt△ACB中,CD⊥AB,又∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD.
又∵AD∶BD=2∶3,
令AD=2x,BD=3x(x>0),答案 C12341.如图,在△ABC中,∠ACB=90°,CD⊥AB于
点D,下列说法中正确的个数是( )
①AC·BC=AB·CD ②AC2=AD·DB
③BC2=BD·BA ④CD2=AD·DB
A.1 B.2 C.3 D.3解析 ∵在△ABC中,∠ACB=90°,CD⊥AB,1234由BC2=BD·BA,知③正确;
∵△ACD∽△CBD,∴AC2=AD·AB,CD2=AD·DB,故②错误,④正确.
正确的个数是3个.故选C.
答案 C12342.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AD=3,BD=2,则AC与BC的比是( )1234解析 ∵在△ABC中,∠ACB=90°,CD⊥AB,
由射影定理,得AC2=AD·AB,BC2=BD·BA,
∴AC2∶BC2=AD∶BD=3∶2.答案 D12343.如图,在Rt△ABC中,∠ACB=90°,CD⊥
AB,AC=6,AD=3.6,则BC=________.解析 由题意知AC2=AD·AB,812344.如图,在△ABC中,CD⊥AB于D,若CD2=AD·BD,求证:△ABC为直角三角形.1234证明 ∵CD⊥AB,∴∠CDA=∠BDC=90°.
又∵CD2=AD·BD,即AD∶CD=CD∶BD,
∴△ACD∽△CBD.∴∠CAD=∠BCD.
又∵∠ACD+∠CAD=90°,
∴∠ACB=∠ACD+∠BCD=∠ACD+∠CAD=90°,
即△ABC为直角三角形.课堂小结1.(1)点在直线上的射影就是由点向直线引垂线,垂足即为射影;
(2)线段在直线上的射影就是由线段的两端点向直线引垂线,两垂足间的线段就是所求射影.
2.应用射影定理有两个条件:一是直角三角形;二是斜边上的高.应用射影定理可求直角三角形的边长、面积等有关量,还可研究相似问题、比例式等问题.3.直角三角形射影定理的逆定理
如果一个三角形一边上的高是另两边在这条边上的射影的比例中项,那么这个三角形是直角三角形.1234一、基础达标56789101112131.在△ABC中,∠BAC=90°,AD是BC边上的高,
则相似三角形共有( )
A.0对 B.1对
C.2对 D.3对解析 如题图所示,△ACD∽△BAD,△ACD∽△BCA,△ABD∽△CBA,共有3对.D123456789101112132.在Rt△ACB中,∠C=90°,CD⊥AB于D,若BD∶AD=1∶4,则tan∠BCD的值是( )解析 如图所示,由射影定理得CD2=AD·BD,
又∵BD∶AD=1∶4,令BD=x,则AD=4x(x>0).
∴CD2=AD·BD=4x2,∴CD=2x,C1234567891011121312345678910111213解析 由题意得,CD2=AD·BD,又AC2=AD·AB,BC2=BD·AB,答案 A123456789101112134.在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.若BC=m,∠B=α,则AD的长为( )
A.msin2α B.mcos2α
C.msin αcos α D.msin αtan α12345678910111213解析 由射影定理,得AB2=BD·BC,AC2=CD·BC,
即m2cos2α=BD·m,m2sin2α=CD·m,
即BD=mcos2α,CD=msin2α.
又∵AD2=BD·DC=m2cos2αsin2α,
∴AD=mcos αsin α.故选C.
答案 C123456789101112135.如图,AB是半圆O的直径,C是半圆O上异于A,B的点,CD⊥AB,垂足为D,已知AD=2,CB= ,则CD=___________.12345678910111213解析 ∵AB是半圆O的直径,
∴△ABC是直角三角形,CD是斜边上的一条高,123456789101112136.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=4,sin∠ACD= ,则CD=______,BC=________.12345678910111213得AC=5,12345678910111213123456789101112137.如图所示,在△ABC中,AD⊥BC于D,BE平分∠ABC交AC于E,EF⊥BC于F,且BD·CF2=CD·EF2.求证:EF∶DF=BC∶AC.12345678910111213证明 ∵AD⊥BC,EF⊥BC,∴EF∥AD.即AD2=BD·CD,∴∠BAC=90°.∴AC2=BC·CD.
∵BE平分∠ABC,EA⊥AB,EF⊥BC,∴AE=EF.12345678910111213即EF∶DF=BC∶AC.二、能力提升123456789101112138.设P1,…,Pn为平面α内的n个点,在平面α内的所有点中,若点P到点P1,P2,…,Pn的距离之和最小,则称点P为点P1,P2,…,Pn的一个“中位点”,例如,线段AB上的任意点都是端点A,B的中位点.则有下列命题:
①若三个点A,B,C共线,C在线段AB上,则C是A,B,C的中位点;12345678910111213②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点A,B,C,D共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是____________.(写出所有真命题的序号)12345678910111213解析 ①若三个点A、B、C共线,C在线段AB上,根据两点之间线段最短,则C是A,B,C的中位点,正确;
②举一个反例,如边长为3,4,5的直角三角形ABC,此直角三角形的斜边的中点到三个顶点的距离之和为5+2.5=7.5,而直角顶点到三个顶点的距离之和为7,
所以直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;12345678910111213③若四个点A、B、C、D共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;
④如图,在梯形ABCD中,对角线的交点
为O,P是任意一点,则根据三角形两边
之和大于第三边得PA+PB+PC+PD≥
AC+BD=OA+OB+OC+OD,12345678910111213所以梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故答案为:①④.
答案 ①④123456789101112139.如图,圆O上一点C在直径AB上的射影为D,点D在半径OC上的射影为E.若AB=3AD,则 的值为___________.12345678910111213解析 设圆的半径为R,在Rt△ODC中,∵DE⊥OC,
由射影定理得OD2=OE·OC,答案 81234567891011121310.如图所示,D为△ABC中BC边上的一点,∠CAD=∠B,若AD=6,AB=10,BD=8,则CD的长为___________.12345678910111213解析 在△ABD中,AD=6,AB=10,BD=8,
满足AB2=AD2+BD2,∴∠ADB=90°,
即AD⊥BC.又∵∠CAD=∠B,且∠C+∠CAD=90°.
∴∠C+∠B=90°,即∠BAC=90°,
故在Rt△BAC中,AD⊥BC,12345678910111213由射影定理知AD2=BD·CD,1234567891011121311.如图,CD是Rt△ABC的斜边AB上的高线.
求证:CD·AC=BC·AD.
证明 在Rt△ABC中,∵CD⊥AB,
∴CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.
∴CD2·AC2=BD·AB·AD2=BC2·AD2.
∴CD·AC=BC·AD.1234567891011121312.已知BD、CE是△ABC的两条高,过点D的直线交BC和BA的延长线于G、H,交CE于F,且∠H=∠BCE. 求证:GD2=GF·GH.12345678910111213证明 ∵∠H=∠BCE,∠CBE=∠HBG,
∴△BCE∽△BHG.又 CE⊥BH,
∴∠BGH=∠BEC=90°,
∴HG⊥BC .
∵BD⊥AC,在Rt△BCD中,
由射影定理得,GD2=BG·CG, ①
∵∠H=∠BCF, ∠FGC=∠BGH=90°,12345678910111213∴BG·GC=GH·FG. ②
由①②得,GD2=GH·FG.三、探究与创新1234567891011121313.如图,已知Rt△ABC的周长为48 cm,一锐角平分线分对边为3∶5两部分.12345678910111213(1)求直角三角形的三边长;
解 如图,设CD=3x,BD=5x,则BC=8x,
过D作DE⊥AB于点E,
由Rt△ADC≌Rt△ADE可知,
DE=3x,BE=4x,
∴AE+AC+12x=48,12345678910111213又AE=AC,
∴AC=24-6x,AB=24-2x,
∴(24-6x)2+(8x)2=(24-2x)2,
解得:x1=0(舍去),x2=2,
∴AB=20,AC=12,BC=16,
∴三边长分别为:20 cm,12 cm,16 cm.12345678910111213(2)求两直角边在斜边上的射影的长.
解 作CF⊥AB于F点,∴AC2=AF·AB,
1.理解直角三角形的射影定理.
2.理解直角三角形射影定理的逆定理.
3.能应用直角三角形的射影定理及其逆定理解决相关的几何问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功4分层训练 解疑纠偏,训练检测[知识链接]已知:如图,∠ACB=90°,CD⊥AB于D. (1)图中有几条线段? 答案 6条,分别记为AB,AC,BC,CD,AD,BD. (2)图中有几对相似三角形?可写出几组比例式?
答案 由图中△ACD∽△CBD∽△ABC,可分别写出三组比例式:(3)有几个带有比例中项的比例式?由上可得到哪些等积式?
答案 只有三个比例中项的表达式:可得到等积式:CD2=AD·BD,BC2=BD·BA,AC2=AD·AB .[预习导引]1.射影的有关概念
(1)点在直线上的正射影:从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的 .
(2)线段在直线上的正射影:一条线段在直线上的正射影,是指线段的两个端点在这条直线上的正射影间的线段.正射影2.直角三角形的射影定理
(1)直角三角形的射影定理:直角三角形斜边上的高是两直角边在斜边上射影的 ;两直角边分别是它们在斜边上射影与斜边的 .
(2)符号表示:如图,CD是Rt△ABC的斜边AB
上的高,则AC2= ;BC2= ;CD2
= .比例中项比例中项AD·ABBD·BAAD·BD要点一 用射影定理求线段的长例1 如图,圆O上一点C在直径AB上的射影为D,AD=2,DB=8,求CD,AC和BC的长.解 ∵∠ACB是半圆上的圆周角,∴∠ACB=90°,
即△ABC是直角三角形.
由射影定理可得
CD2=AD·BD=2×8=16,解得CD=4,规律方法 应用射影定理有两个条件:一是直角三角形;二是斜边上的高.在求直角三角形的边长时,根据已知的条件,可以应用射影定理,有时也可应用勾股定理.跟踪演练1 在△ABC中,AC⊥BC,CD⊥AB于点D,若AD=27,BD=3,则AC=__________,BC=__________,
CD=________.
解析 由射影定理,得CD2=AD·BD,则CD=9.
根据勾股定理,得9要点二 用射影定理证明等式例2 如图所示,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DF⊥AC于F,DE⊥AB于E.试证明:(1)AB·AC=AD·BC;证明 在Rt△ABC中,AD⊥BC,∴AB·AC=BC·AD.(2)AD3=BC·BE·CF.
证明 在Rt△ADB中,DE⊥AB,
由射影定理得BD2=BE·AB.
同理CD2=CF·AC,
∴BD2·CD2=BE·AB·CF·AC. ①
又在Rt△BAC中,AD⊥BC,
∴AD2=BD·DC, ②∴由①②两式得AD4=BE·CF·AB·AC,由(1)知AB·AC=BC·AD代入上式得AD3=BE·CF·BC.规律方法 利用直角三角形的射影定理证明恒等式
(1)结合图形,仔细分析题目的结论;
(2)由于射影定理中可供选择的等式较多,需要合理选择.跟踪演练2 如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F.求证:AE·AB=AF·AC.证明 因为AD⊥BC,所以△ADB与△ADC都是直角三角形.
在Rt△ADB中,由于DE⊥AB于E,
所以AD2=AB·AE;
在Rt△ADC中,由于DF⊥AC于F,
所以AD2=AF·AC,
所以AE·AB=AF·AC.要点三 射影定理的综合应用例3 如图所示,在△ABC中,D、F分别在AC、BC上,且AB⊥AC,AF⊥BC,BD=DC=FC=1,求AC.解 在△ABC中,设AC为x,
∵AB⊥AC,AF⊥BC,又FC=1,
根据射影定理,得AC2=FC·BC,即BC=x2.
再由射影定理,得AF2=BF·FC=(BC-FC)·FC,在△BDC中,过D作DE⊥BC于E,
∵BD=DC=1,∴BE=EC,在Rt△DEC中,∵DE2+EC2=DC2,规律方法 (1)由射影定理可得三角形相似,可求相似比、三角形边长等.
(2)射影定理中有三个等式,根据题目需要恰当地进行选择.跟踪演练3 在△ABC中,∠ACB=90°,CD⊥AB于D,AD∶BD=2∶3,则△ACD与△CBD的相似比为( )
A.2∶3 B.4∶9
C. ∶3 D.不确定解析 如题图,在Rt△ACB中,CD⊥AB,又∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD.
又∵AD∶BD=2∶3,
令AD=2x,BD=3x(x>0),答案 C12341.如图,在△ABC中,∠ACB=90°,CD⊥AB于
点D,下列说法中正确的个数是( )
①AC·BC=AB·CD ②AC2=AD·DB
③BC2=BD·BA ④CD2=AD·DB
A.1 B.2 C.3 D.3解析 ∵在△ABC中,∠ACB=90°,CD⊥AB,1234由BC2=BD·BA,知③正确;
∵△ACD∽△CBD,∴AC2=AD·AB,CD2=AD·DB,故②错误,④正确.
正确的个数是3个.故选C.
答案 C12342.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AD=3,BD=2,则AC与BC的比是( )1234解析 ∵在△ABC中,∠ACB=90°,CD⊥AB,
由射影定理,得AC2=AD·AB,BC2=BD·BA,
∴AC2∶BC2=AD∶BD=3∶2.答案 D12343.如图,在Rt△ABC中,∠ACB=90°,CD⊥
AB,AC=6,AD=3.6,则BC=________.解析 由题意知AC2=AD·AB,812344.如图,在△ABC中,CD⊥AB于D,若CD2=AD·BD,求证:△ABC为直角三角形.1234证明 ∵CD⊥AB,∴∠CDA=∠BDC=90°.
又∵CD2=AD·BD,即AD∶CD=CD∶BD,
∴△ACD∽△CBD.∴∠CAD=∠BCD.
又∵∠ACD+∠CAD=90°,
∴∠ACB=∠ACD+∠BCD=∠ACD+∠CAD=90°,
即△ABC为直角三角形.课堂小结1.(1)点在直线上的射影就是由点向直线引垂线,垂足即为射影;
(2)线段在直线上的射影就是由线段的两端点向直线引垂线,两垂足间的线段就是所求射影.
2.应用射影定理有两个条件:一是直角三角形;二是斜边上的高.应用射影定理可求直角三角形的边长、面积等有关量,还可研究相似问题、比例式等问题.3.直角三角形射影定理的逆定理
如果一个三角形一边上的高是另两边在这条边上的射影的比例中项,那么这个三角形是直角三角形.1234一、基础达标56789101112131.在△ABC中,∠BAC=90°,AD是BC边上的高,
则相似三角形共有( )
A.0对 B.1对
C.2对 D.3对解析 如题图所示,△ACD∽△BAD,△ACD∽△BCA,△ABD∽△CBA,共有3对.D123456789101112132.在Rt△ACB中,∠C=90°,CD⊥AB于D,若BD∶AD=1∶4,则tan∠BCD的值是( )解析 如图所示,由射影定理得CD2=AD·BD,
又∵BD∶AD=1∶4,令BD=x,则AD=4x(x>0).
∴CD2=AD·BD=4x2,∴CD=2x,C1234567891011121312345678910111213解析 由题意得,CD2=AD·BD,又AC2=AD·AB,BC2=BD·AB,答案 A123456789101112134.在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.若BC=m,∠B=α,则AD的长为( )
A.msin2α B.mcos2α
C.msin αcos α D.msin αtan α12345678910111213解析 由射影定理,得AB2=BD·BC,AC2=CD·BC,
即m2cos2α=BD·m,m2sin2α=CD·m,
即BD=mcos2α,CD=msin2α.
又∵AD2=BD·DC=m2cos2αsin2α,
∴AD=mcos αsin α.故选C.
答案 C123456789101112135.如图,AB是半圆O的直径,C是半圆O上异于A,B的点,CD⊥AB,垂足为D,已知AD=2,CB= ,则CD=___________.12345678910111213解析 ∵AB是半圆O的直径,
∴△ABC是直角三角形,CD是斜边上的一条高,123456789101112136.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=4,sin∠ACD= ,则CD=______,BC=________.12345678910111213得AC=5,12345678910111213123456789101112137.如图所示,在△ABC中,AD⊥BC于D,BE平分∠ABC交AC于E,EF⊥BC于F,且BD·CF2=CD·EF2.求证:EF∶DF=BC∶AC.12345678910111213证明 ∵AD⊥BC,EF⊥BC,∴EF∥AD.即AD2=BD·CD,∴∠BAC=90°.∴AC2=BC·CD.
∵BE平分∠ABC,EA⊥AB,EF⊥BC,∴AE=EF.12345678910111213即EF∶DF=BC∶AC.二、能力提升123456789101112138.设P1,…,Pn为平面α内的n个点,在平面α内的所有点中,若点P到点P1,P2,…,Pn的距离之和最小,则称点P为点P1,P2,…,Pn的一个“中位点”,例如,线段AB上的任意点都是端点A,B的中位点.则有下列命题:
①若三个点A,B,C共线,C在线段AB上,则C是A,B,C的中位点;12345678910111213②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点A,B,C,D共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是____________.(写出所有真命题的序号)12345678910111213解析 ①若三个点A、B、C共线,C在线段AB上,根据两点之间线段最短,则C是A,B,C的中位点,正确;
②举一个反例,如边长为3,4,5的直角三角形ABC,此直角三角形的斜边的中点到三个顶点的距离之和为5+2.5=7.5,而直角顶点到三个顶点的距离之和为7,
所以直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;12345678910111213③若四个点A、B、C、D共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;
④如图,在梯形ABCD中,对角线的交点
为O,P是任意一点,则根据三角形两边
之和大于第三边得PA+PB+PC+PD≥
AC+BD=OA+OB+OC+OD,12345678910111213所以梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故答案为:①④.
答案 ①④123456789101112139.如图,圆O上一点C在直径AB上的射影为D,点D在半径OC上的射影为E.若AB=3AD,则 的值为___________.12345678910111213解析 设圆的半径为R,在Rt△ODC中,∵DE⊥OC,
由射影定理得OD2=OE·OC,答案 81234567891011121310.如图所示,D为△ABC中BC边上的一点,∠CAD=∠B,若AD=6,AB=10,BD=8,则CD的长为___________.12345678910111213解析 在△ABD中,AD=6,AB=10,BD=8,
满足AB2=AD2+BD2,∴∠ADB=90°,
即AD⊥BC.又∵∠CAD=∠B,且∠C+∠CAD=90°.
∴∠C+∠B=90°,即∠BAC=90°,
故在Rt△BAC中,AD⊥BC,12345678910111213由射影定理知AD2=BD·CD,1234567891011121311.如图,CD是Rt△ABC的斜边AB上的高线.
求证:CD·AC=BC·AD.
证明 在Rt△ABC中,∵CD⊥AB,
∴CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.
∴CD2·AC2=BD·AB·AD2=BC2·AD2.
∴CD·AC=BC·AD.1234567891011121312.已知BD、CE是△ABC的两条高,过点D的直线交BC和BA的延长线于G、H,交CE于F,且∠H=∠BCE. 求证:GD2=GF·GH.12345678910111213证明 ∵∠H=∠BCE,∠CBE=∠HBG,
∴△BCE∽△BHG.又 CE⊥BH,
∴∠BGH=∠BEC=90°,
∴HG⊥BC .
∵BD⊥AC,在Rt△BCD中,
由射影定理得,GD2=BG·CG, ①
∵∠H=∠BCF, ∠FGC=∠BGH=90°,12345678910111213∴BG·GC=GH·FG. ②
由①②得,GD2=GH·FG.三、探究与创新1234567891011121313.如图,已知Rt△ABC的周长为48 cm,一锐角平分线分对边为3∶5两部分.12345678910111213(1)求直角三角形的三边长;
解 如图,设CD=3x,BD=5x,则BC=8x,
过D作DE⊥AB于点E,
由Rt△ADC≌Rt△ADE可知,
DE=3x,BE=4x,
∴AE+AC+12x=48,12345678910111213又AE=AC,
∴AC=24-6x,AB=24-2x,
∴(24-6x)2+(8x)2=(24-2x)2,
解得:x1=0(舍去),x2=2,
∴AB=20,AC=12,BC=16,
∴三边长分别为:20 cm,12 cm,16 cm.12345678910111213(2)求两直角边在斜边上的射影的长.
解 作CF⊥AB于F点,∴AC2=AF·AB,
