人教版选修4-1 1.4直角三角形的射影定理课件(16张)
文档属性
| 名称 | 人教版选修4-1 1.4直角三角形的射影定理课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-14 00:00:00 | ||
图片预览


文档简介
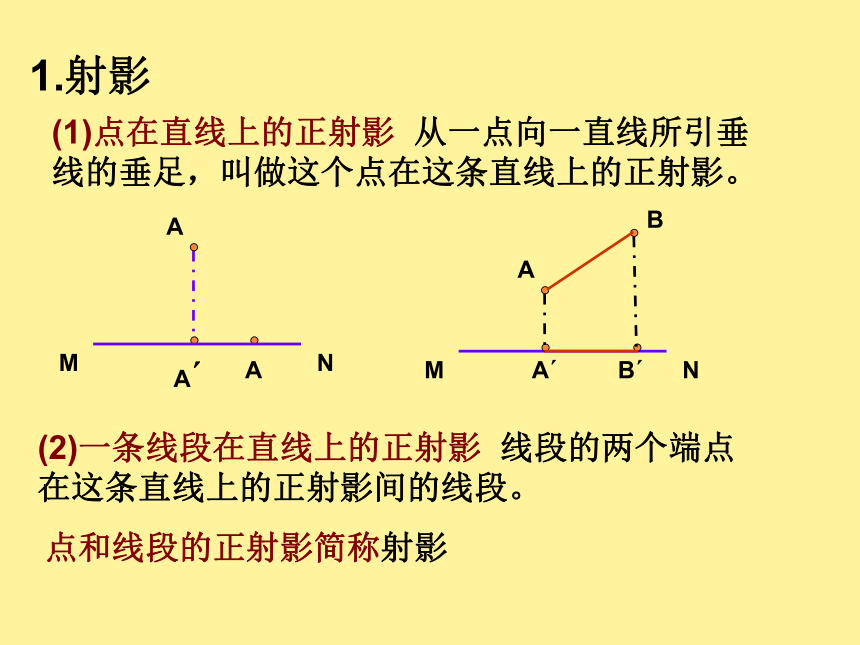
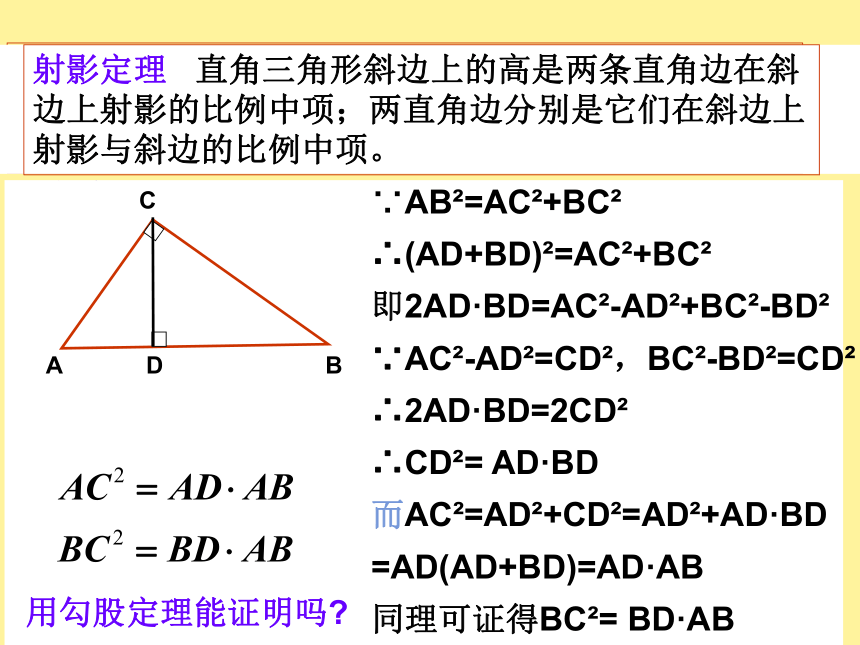
课件16张PPT。1.4 直角三角形的射影定理1.射影(1)点在直线上的正射影 从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的正射影。(2)一条线段在直线上的正射影 线段的两个端点在这条直线上的正射影间的线段。点和线段的正射影简称射影探究:△ABC是直角三角形,CD为斜边AB上的高。你能从射影的角度来考察AC与AD,BC与BD等的关系。你能发现这些线段之间的某些关系吗?∽∽射影定理 直角三角形斜边上的高是两条直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项。用勾股定理能证明吗?∵AB2=AC2+BC2
∴(AD+BD)2=AC2+BC2
即2AD·BD=AC2-AD2+BC2-BD2
∵AC2-AD2=CD2,BC2-BD2=CD2
∴2AD·BD=2CD2
∴CD2= AD·BD
而AC2=AD2+CD2=AD2+AD·BD
=AD(AD+BD)=AD·AB
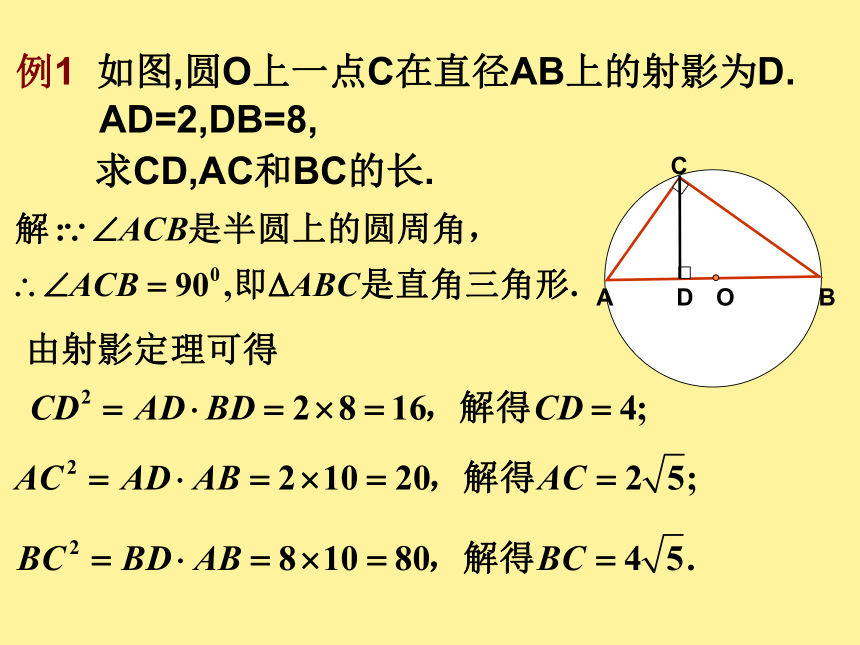
同理可证得BC2= BD·AB例1 如图,圆O上一点C在直径AB上的射影为D.
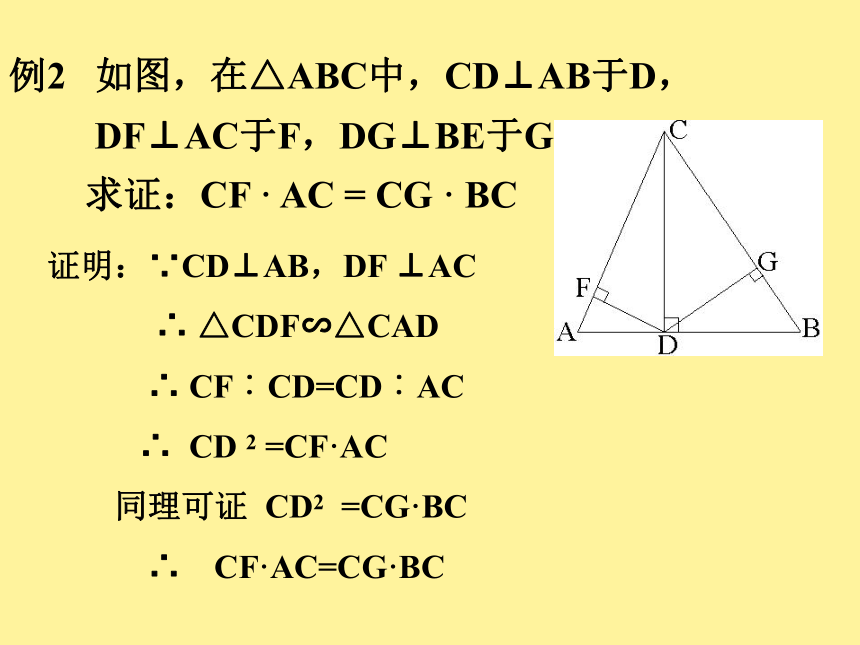
AD=2,DB=8,求CD,AC和BC的长.例2 如图,在△ABC中,CD⊥AB于D,
DF⊥AC于F,DG⊥BE于G。
求证:CF · AC = CG · BC证明:∵CD⊥AB,DF ⊥AC
∴ △CDF∽△CAD
∴ CF︰CD=CD︰AC
∴ CD 2 =CF·AC
同理可证 CD2 =CG·BC
∴ CF·AC=CG·BC 总结:
已知“直角三角形斜边上的高”这一基本
图形中的六条线段中的任意两条线段,就可
以求出其余四条线段,有时需要用到方程的
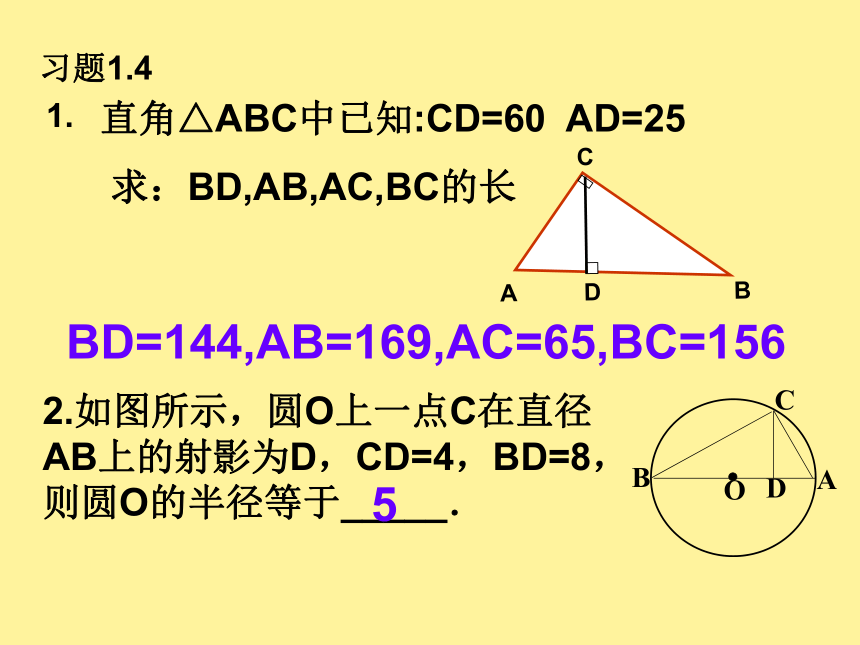
思想。习题1.41.直角△ABC中已知:CD=60 AD=25
求:BD,AB,AC,BC的长BD=144,AB=169,AC=65,BC=1562.如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于_____.5 [例1] 如图,在Rt△ABC中,CD为
斜边AB上的高,若AD=2 cm,DB=6 cm,
求CD,AC,BC的长.
[思路点拨] 在直角三角形内求线段
的长度,可考虑使用勾股定理和射影定理.1.如图,在Rt△ABC中,∠C=90°,
CD是AB上的 高.已知BD=4,
AB=29,试求出图中其他未知线 段的长.总结:
1、知识:学习了直角 三角形中重要的比例式和比例中项的表达式——射影定理。
2、方法:利用射影定理的基本图形求线段和证明线段等积式。
3、能力:会从较复杂的图形中分解出射影定理的基本图形的能力。
4、数学思想:方程思想和转化思想。1.从特殊到一般的思考方法.数学方法: 在研究数学问题时,通过考察特殊性问题获得一般规律的猜想,并从中得到证明一般规律的思想方法的启发;然后由特殊过渡到一般,对一般性结论作出严格证明.2.化归思想方法. 在研究问题时,常常通过一定的逻辑推理,将困难的,不熟悉的问题转化为容易的熟悉的问题.恒等变形,换元法,数形结合法,参数法等,都是具体的化归方法.相似三角形的证明采用了化归为预备定理的方法.
∴(AD+BD)2=AC2+BC2
即2AD·BD=AC2-AD2+BC2-BD2
∵AC2-AD2=CD2,BC2-BD2=CD2
∴2AD·BD=2CD2
∴CD2= AD·BD
而AC2=AD2+CD2=AD2+AD·BD
=AD(AD+BD)=AD·AB
同理可证得BC2= BD·AB例1 如图,圆O上一点C在直径AB上的射影为D.
AD=2,DB=8,求CD,AC和BC的长.例2 如图,在△ABC中,CD⊥AB于D,
DF⊥AC于F,DG⊥BE于G。
求证:CF · AC = CG · BC证明:∵CD⊥AB,DF ⊥AC
∴ △CDF∽△CAD
∴ CF︰CD=CD︰AC
∴ CD 2 =CF·AC
同理可证 CD2 =CG·BC
∴ CF·AC=CG·BC 总结:
已知“直角三角形斜边上的高”这一基本
图形中的六条线段中的任意两条线段,就可
以求出其余四条线段,有时需要用到方程的
思想。习题1.41.直角△ABC中已知:CD=60 AD=25
求:BD,AB,AC,BC的长BD=144,AB=169,AC=65,BC=1562.如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于_____.5 [例1] 如图,在Rt△ABC中,CD为
斜边AB上的高,若AD=2 cm,DB=6 cm,
求CD,AC,BC的长.
[思路点拨] 在直角三角形内求线段
的长度,可考虑使用勾股定理和射影定理.1.如图,在Rt△ABC中,∠C=90°,
CD是AB上的 高.已知BD=4,
AB=29,试求出图中其他未知线 段的长.总结:
1、知识:学习了直角 三角形中重要的比例式和比例中项的表达式——射影定理。
2、方法:利用射影定理的基本图形求线段和证明线段等积式。
3、能力:会从较复杂的图形中分解出射影定理的基本图形的能力。
4、数学思想:方程思想和转化思想。1.从特殊到一般的思考方法.数学方法: 在研究数学问题时,通过考察特殊性问题获得一般规律的猜想,并从中得到证明一般规律的思想方法的启发;然后由特殊过渡到一般,对一般性结论作出严格证明.2.化归思想方法. 在研究问题时,常常通过一定的逻辑推理,将困难的,不熟悉的问题转化为容易的熟悉的问题.恒等变形,换元法,数形结合法,参数法等,都是具体的化归方法.相似三角形的证明采用了化归为预备定理的方法.
