人教版选修4-1 2.1圆周角定理课件课件(17张)
文档属性
| 名称 | 人教版选修4-1 2.1圆周角定理课件课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 164.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-14 22:24:03 | ||
图片预览

文档简介
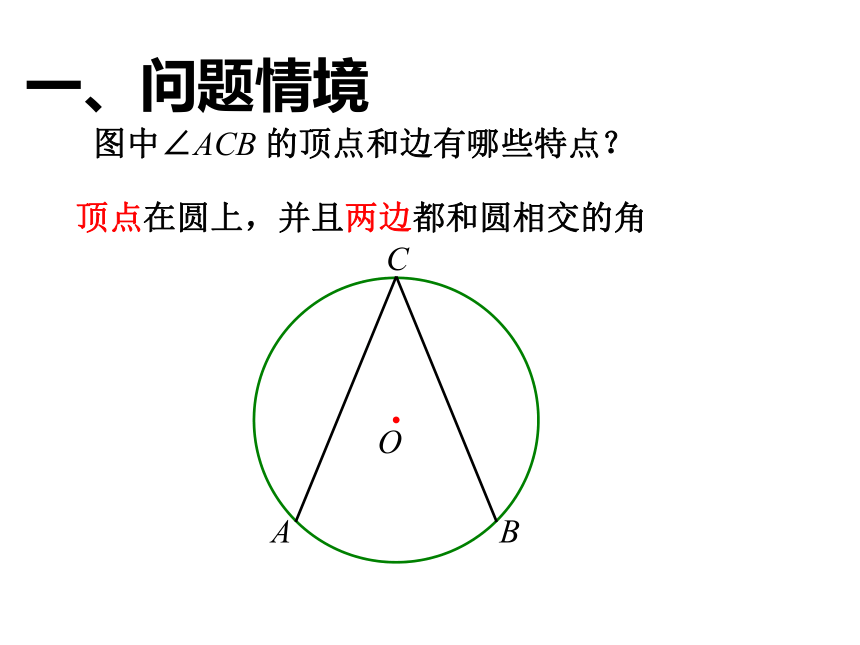
课件17张PPT。 圆周角定理 图中∠ACB 的顶点和边有哪些特点?
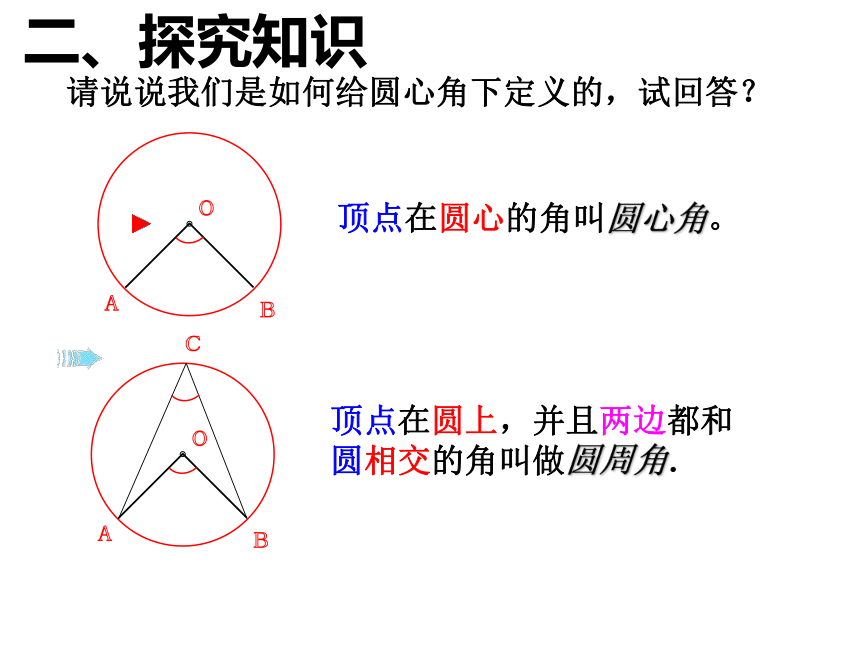
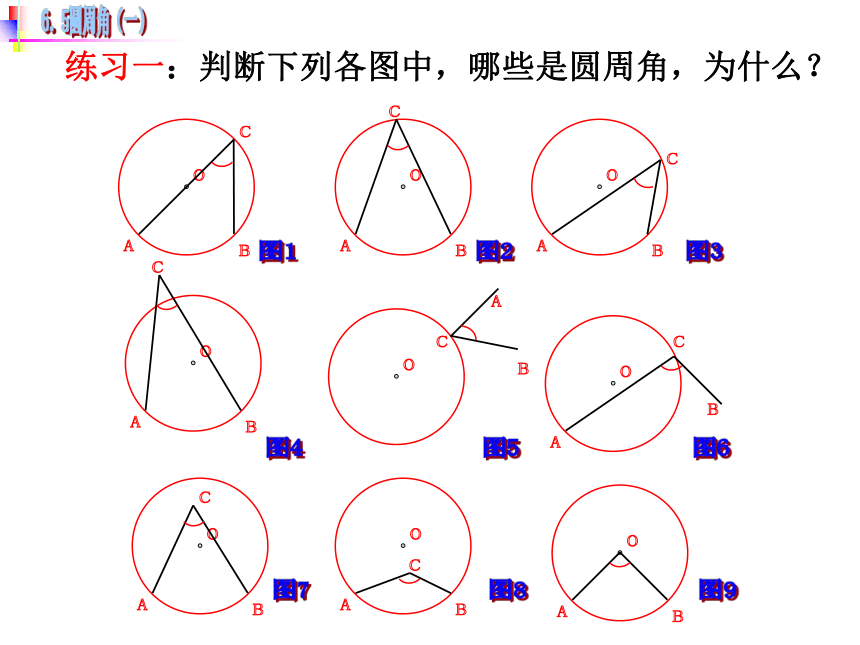
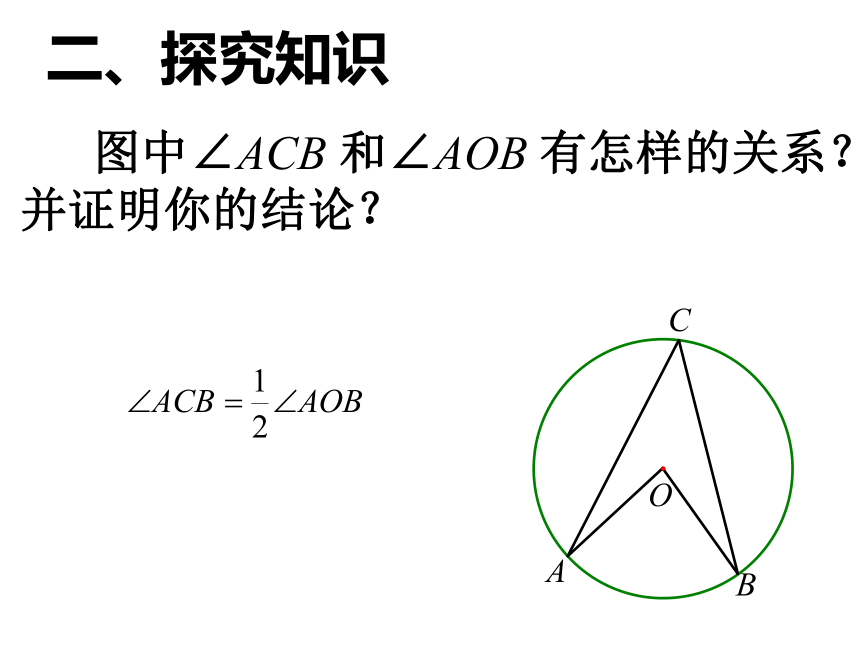
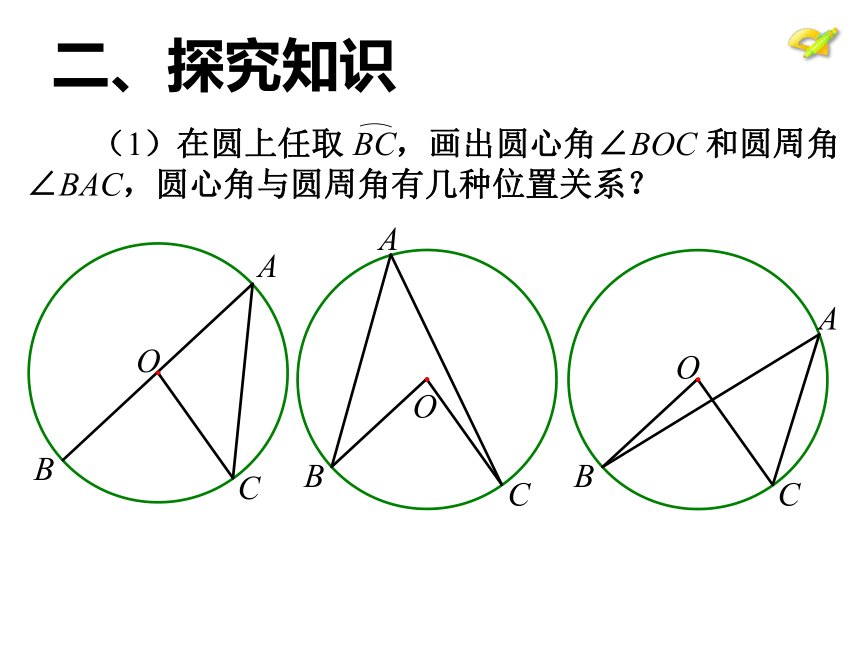
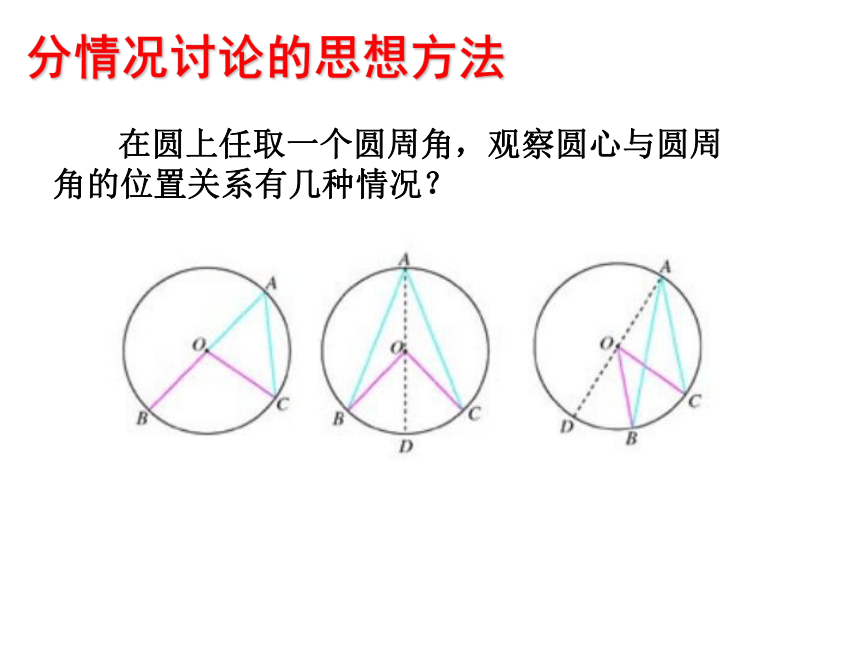
顶点在圆上,并且两边都和圆相交的角一、问题情境请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角。顶点在圆上,并且两边都和圆相交的角叫做圆周角. 二、探究知识练习一:判断下列各图中,哪些是圆周角,为什么? oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9 图中∠ACB 和∠AOB 有怎样的关系?并证明你的结论?二、探究知识二、探究知识分情况讨论的思想方法 在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况? (2)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?二、探究知识 证明猜想 我们来分析上页的前两种情况,第三种情况请同学们完成证明. (3)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?D证明:如图,连接 AO 并延长交⊙O 于点 D.∵ OA=OB,
∴ ∠BAD=∠B. 又∵ ∠BOD=∠BAD+∠B,二、探究知识 证明猜想 思考:
一条弧所对的圆周角之间有什么关系?同弧或等弧 所对的圆周角之间有什么关系? 同弧或等弧所对的圆周角相等.二、探究知识 探究2·ABC1OC2C3·ABCO二、探究知识 例、如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ?ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.解:连接 OD,AD,BD, 三、应用新知 问题1 如图1,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?图1 问题2 如图2,圆周角∠BAC=90o,弦BC经过圆心O吗?为什么?四、巩固新知 1.如图,AB是⊙O的直径,∠A=10°,
则∠ABC=________.四、巩固新知 2.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.60°50°四、巩固新知 3.已知:BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,AE=AB,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由. ((四、巩固新知 4.如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状: . 四、巩固新知
顶点在圆上,并且两边都和圆相交的角一、问题情境请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角。顶点在圆上,并且两边都和圆相交的角叫做圆周角. 二、探究知识练习一:判断下列各图中,哪些是圆周角,为什么? oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9 图中∠ACB 和∠AOB 有怎样的关系?并证明你的结论?二、探究知识二、探究知识分情况讨论的思想方法 在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况? (2)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?二、探究知识 证明猜想 我们来分析上页的前两种情况,第三种情况请同学们完成证明. (3)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?D证明:如图,连接 AO 并延长交⊙O 于点 D.∵ OA=OB,
∴ ∠BAD=∠B. 又∵ ∠BOD=∠BAD+∠B,二、探究知识 证明猜想 思考:
一条弧所对的圆周角之间有什么关系?同弧或等弧 所对的圆周角之间有什么关系? 同弧或等弧所对的圆周角相等.二、探究知识 探究2·ABC1OC2C3·ABCO二、探究知识 例、如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ?ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.解:连接 OD,AD,BD, 三、应用新知 问题1 如图1,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?图1 问题2 如图2,圆周角∠BAC=90o,弦BC经过圆心O吗?为什么?四、巩固新知 1.如图,AB是⊙O的直径,∠A=10°,
则∠ABC=________.四、巩固新知 2.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.60°50°四、巩固新知 3.已知:BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,AE=AB,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由. ((四、巩固新知 4.如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状: . 四、巩固新知
