人教版选修4-1 2.2圆内接四边形的性质与判定定理课件(28张)
文档属性
| 名称 | 人教版选修4-1 2.2圆内接四边形的性质与判定定理课件(28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 107.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-14 00:00:00 | ||
图片预览



文档简介
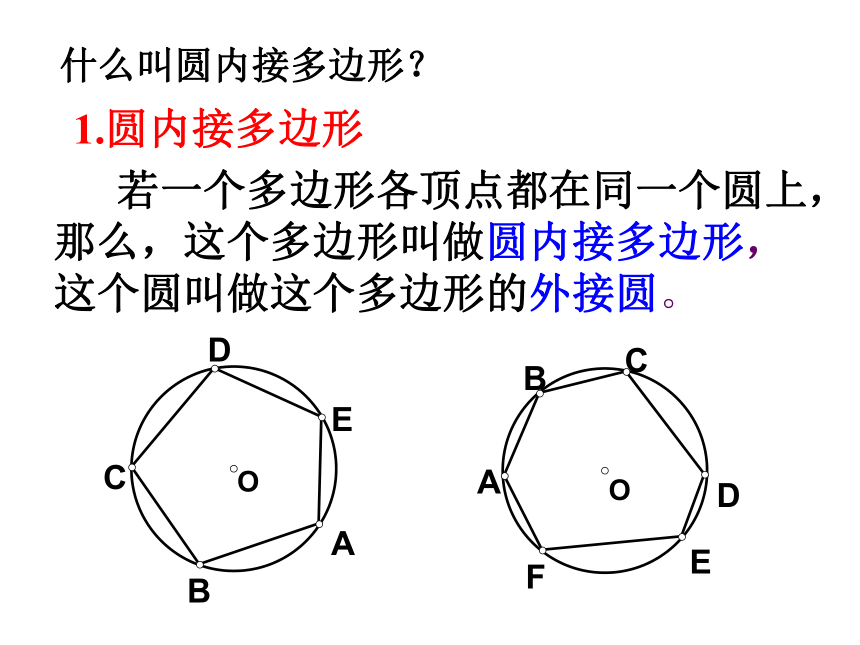
课件28张PPT。二.圆的内接四边形的性质与判定定理第二讲 直线和圆的位置关系1.圆内接多边形 若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。OACDEB什么叫圆内接多边形?回答下列问题:
1.任意三角形都有外接圆吗?. 2.任意正方形有外接圆吗?3.任意矩形是否有外接圆?4. 任意四边形都有外接圆吗?探究:
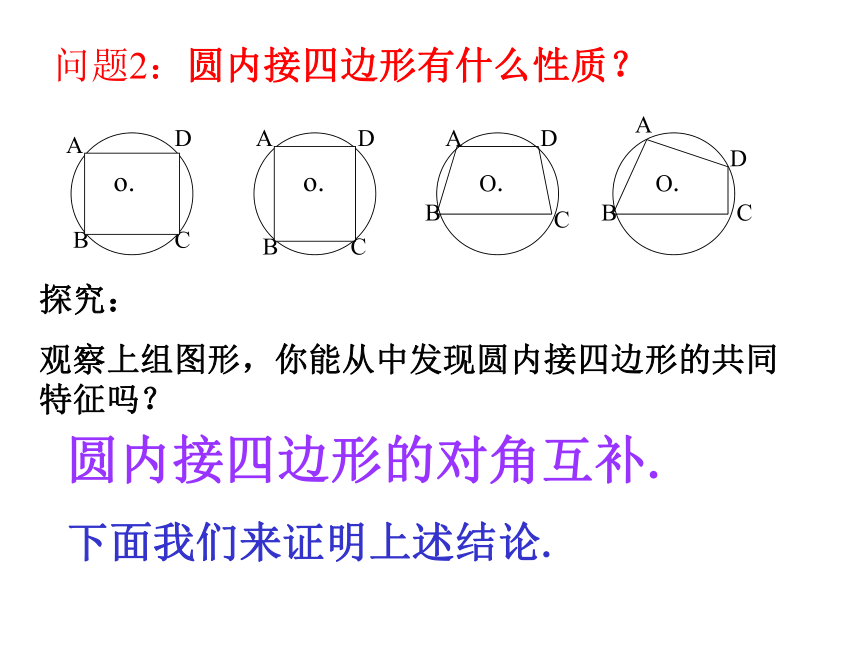
观察上组图形,你能从中发现圆内接四边形的共同特征吗?ABDCO.o.o.ADBCADBCADBC圆内接四边形的对角互补.下面我们来证明上述结论.问题2:圆内接四边形有什么性质?如图,已知四边形ABCD为圆内接四边形;⊙O为四边形ABCD外接圆.求证: ∠A+∠C=180°, ∠B+∠D=180°. 分析:
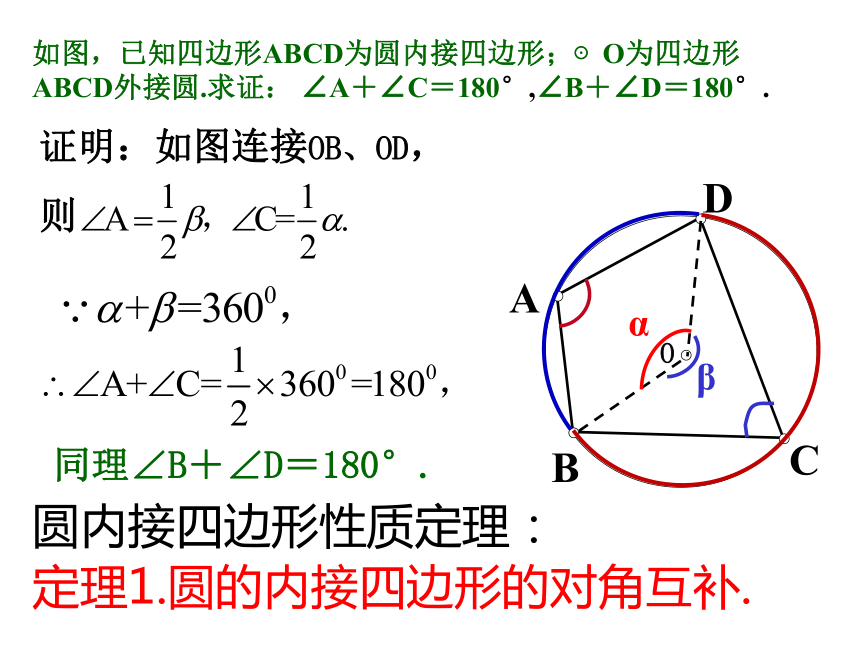
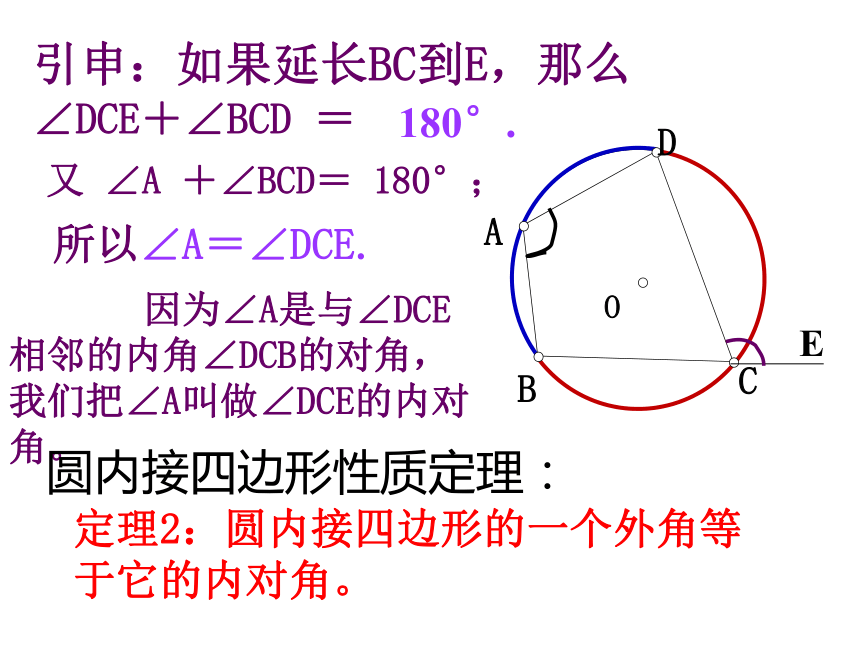
从考察四个角的关系出发,我们发现圆内接四边形的角都是圆周角,因此我们可以借助圆周角定理.CODBA同理∠B+∠D=180°.圆内接四边形性质定理:定理1.圆的内接四边形的对角互补.αβ如图,已知四边形ABCD为圆内接四边形;⊙O为四边形ABCD外接圆.求证: ∠A+∠C=180°,∠B+∠D=180°. 引申:如果延长BC到E,那么∠DCE+∠BCD =180°.所以∠A=∠DCE.又 ∠A +∠BCD= 180°; 因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角。定理2:圆内接四边形的一个外角等于它的内对角。圆内接四边形性质定理:CODBA圆的内接四边形的性质定理: 圆的内接四边形的对角互补,并且任何一个外角都等于它的内角的对角。看右图归纳:练习:1、如图,四边形ABCD为⊙O 的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。∠BAD =50°;∠BCD =130°.例 1. 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。求证:CE∥DF分析: 连结ABABEC是⊙O1的内接四边形ABFD是⊙O2的内接四边形∠E+∠CAB=180°,∠CAB=∠F∠E+∠F=180°CE∥DF证明:连结AB∵ABEC是⊙O1的内接四边形,∴∠1=∠F∵ADFB是⊙O2的内接四边形,∴∠E+∠1=180°∴∠E+∠F=180°∴CE∥DF1例 1. 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。求证:CE∥DF.小结:圆的内接四边形的性质定理: 圆的内接四边形的对角互补,并且任何一个外角都等于它的内角的对角。问题2:如何判定一个四边形有外接圆?2.如果逆命题成立,我们可以得到四边形存在外接圆的判定定理.1.圆内接四边形的性质定理1的逆命题是什么吗? 逆命题:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。如何证明逆命题: 如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。性质定理:圆的内接四边形的对角互补.CODBA如果能够由条件得到⊙O过点D,那么就证明了命题.分析:不在同一直线上的三点确定一个圆。经过A、B、C、三点作⊙O,讨论: ⊙O与点D有几种位置关系?三种:(1)点D在圆⊙O外;(2)点D在圆⊙O内;(3)点D在圆⊙O上.如果我们否定了点D在圆⊙O外和点D在圆⊙O内;则点D在圆⊙O上成立;如何否定了点D在圆⊙O外和点D在圆⊙O内?采用反证法把点D在圆⊙O外和点D在圆⊙O内情况一一否定。已知:在四边形ABCD中,∠B+∠D=180°,求证:A,B,C,D四点在同一个圆周上(简称四点共圆).CODBA反证法证明:(1)假设点D在圆⊙O外;E设E是AD与圆周的交点,连接EC,则有∠AEC+∠B=180°.由题设∠B+∠D=180°.可得∠D=∠AEC.这与“三角形的外角大于任意不相邻的内角”矛盾.故D点不可能在圆外.反证法证明:(2)假设点D在圆⊙O内;CODBA显然AD的延长线必与圆相交,设交点为E,连接CE,则有∠B+∠E =180°.∵∠B+∠D=180°.∴∠E=∠ADC.这与“三角形的外角大于任意不相邻的内角”矛盾.∴D点不可能在圆内.综上所述,点D只能在圆周上,即A、B、C、D四点共圆.定理: 如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。圆内接四边形的判定定理:回顾: 在圆内接四边形判定定理的证明中,我们用分类思想对点D与A、B、C三点确定的圆的位置关系进行了讨论,在每一种情形中都运用了反证法进行了证明.穷举法: 当问题的结论存在多种情形时,通过对每一种情形分别论证,最后获证结论的方法,称为穷举法.这种证明问题的方法叫穷举法.圆内接四边形的判定定理的推论:推论: 如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆。(如何证明?)证明:∵∠BCD+∠DCE=180°,又∵∠A=∠DCE,∴∠BCD+∠A=180°,∴A、B、 C、D四点共圆.圆内接四边形的判定定理:定理: 如果一个四边形的对角互补,或一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.例2.如图,CF是△ABC的AB边上的高,FP⊥BC, FQ⊥AC.求证:A、B、P、Q四点共圆.CABQPF分析:只需说明A、B、P、Q四点确定的四边形的对角互补或外角等于内对角,因此需连接QP.证明:连接QP.在四边形QFPC中,∵ FP⊥BC , FQ⊥AC,∴∠FQA=∠FPC,∴ Q、F、P、C四点共圆.∴∠QFC=∠QPC,又∵CF⊥AB ,∴∠QFC与∠QFA互余.而∠A与∠QFA也互余.∴∠A=∠QFC,∴∠A=∠QPC,∴A、B、P、Q四点共圆.小结:圆内接四边形的性质与判定定理.1.性质定理:2.判定定理:课后作业:课本P30习题2.2:1,2,3. 圆的内接四边形的对角互补,并且任何一个外角都等于它的内角的对角。 如果一个四边形的对角互补,或一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.再见!再见!再见!再见!再见!再见!再见!再见!二圆内接四边形的 性质和判定定理补充习题补充2.如图,在正方形ABCD中,M为AB上一点, N为BC上一点,且BM=BN,BP⊥MC于点P,求证:(1)△BPN∽△CPD;(2)DP⊥NP.分析(1):欲证△BPN∽△CPD;而∠DCP=∠BMC =∠CBP(为什么?)又Rt△MPB∽Rt△BPC;又BM=BN,BC=DC;故△BPN∽△CPD成立;分析(2):欲证DP⊥NP.需证∠DPN= ∠DPC+ ∠NPC=90°;由(1)知∠DPC= ∠BPN°;而∠BPN+ ∠NPC=90°;则∠DPN= ∠DPC+ ∠NPC=90°成立;即DP⊥NP成立. 圆内接四边形性质定理 圆内接四边形对角互补 如果一个多边形的所有顶点都在一个圆上,这个多边形就叫做圆内接多边形,这个圆就是多边形的外接圆DBAC·O 圆内接四边形判定定理 对角互补的四边形内接于圆 一个四边形内接于圆也称这个四边形的顶点四点共圆 定理 若两点在一条线段同侧且对该线段张角相等,则此两点与线段两个端点共圆 特别的,对定线段张角为直角的点共圆 例1、如图,⊙O1与⊙O2交于点M、N,直线AB过M与⊙O1与⊙O2 分别交于点A、B,直线CD过N与⊙O1与⊙O2 分别交于点C、D,求证:AC//BDDBO1·ACMN·O2 例2、如图,D为△ABC的边BC上一点,⊙O1经过点B、D,交AB于另一点E,⊙O2 经过点C、D,交AC于另一点F,⊙O1与⊙O2 交于点G,求证:(1)∠BAC+∠EGF=180°CFO1·ABGD·O2 (2)∠EAG=∠EFG E 例3、如图,以锐角三角形ABC的三边为边向外作三个等边三角形ABD、BCE、CAG,求证:△ABD、△BCE、△CAG的外接圆⊙O1 、⊙O2、⊙O3交于一点·O2A·O3CEBO1·GD
1.任意三角形都有外接圆吗?. 2.任意正方形有外接圆吗?3.任意矩形是否有外接圆?4. 任意四边形都有外接圆吗?探究:
观察上组图形,你能从中发现圆内接四边形的共同特征吗?ABDCO.o.o.ADBCADBCADBC圆内接四边形的对角互补.下面我们来证明上述结论.问题2:圆内接四边形有什么性质?如图,已知四边形ABCD为圆内接四边形;⊙O为四边形ABCD外接圆.求证: ∠A+∠C=180°, ∠B+∠D=180°. 分析:
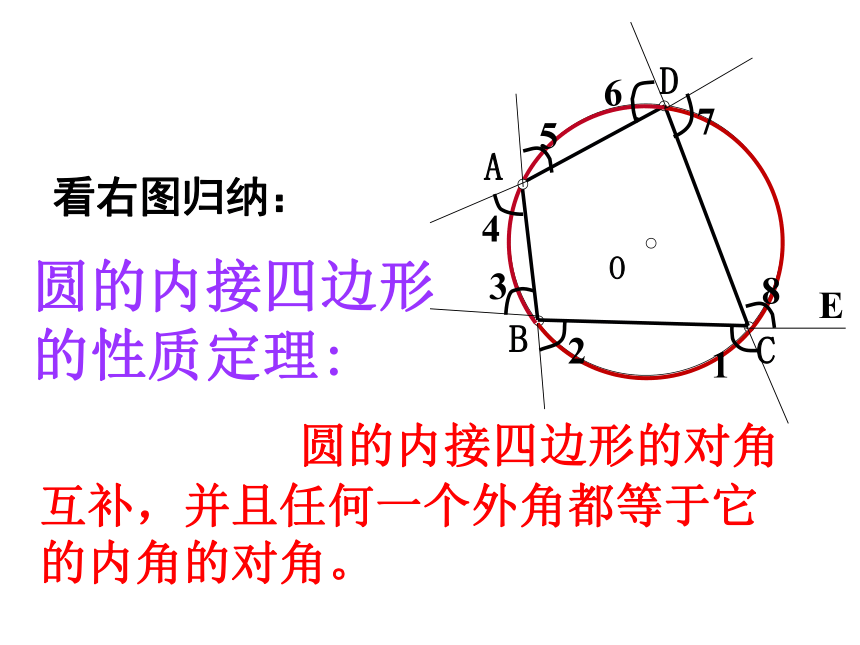
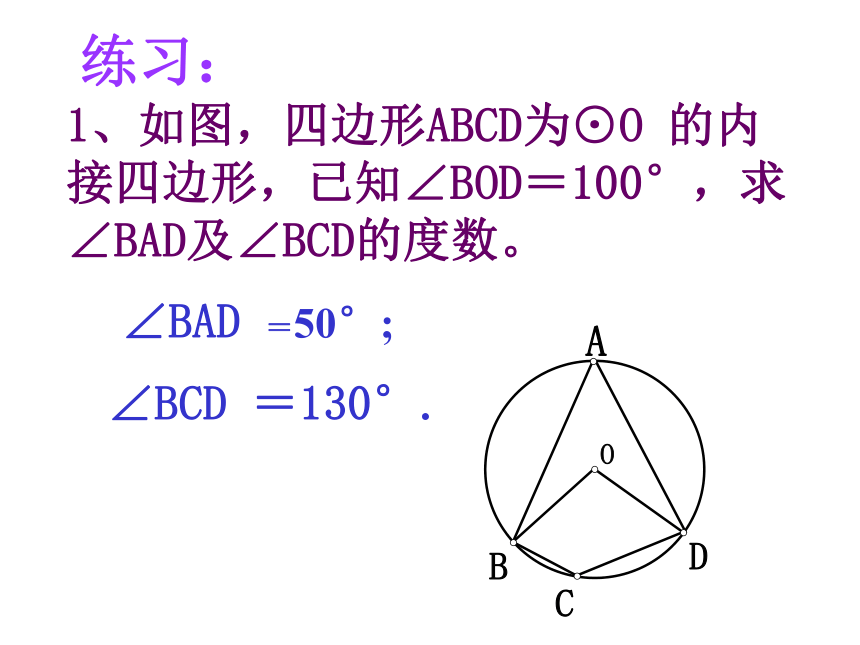
从考察四个角的关系出发,我们发现圆内接四边形的角都是圆周角,因此我们可以借助圆周角定理.CODBA同理∠B+∠D=180°.圆内接四边形性质定理:定理1.圆的内接四边形的对角互补.αβ如图,已知四边形ABCD为圆内接四边形;⊙O为四边形ABCD外接圆.求证: ∠A+∠C=180°,∠B+∠D=180°. 引申:如果延长BC到E,那么∠DCE+∠BCD =180°.所以∠A=∠DCE.又 ∠A +∠BCD= 180°; 因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角。定理2:圆内接四边形的一个外角等于它的内对角。圆内接四边形性质定理:CODBA圆的内接四边形的性质定理: 圆的内接四边形的对角互补,并且任何一个外角都等于它的内角的对角。看右图归纳:练习:1、如图,四边形ABCD为⊙O 的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。∠BAD =50°;∠BCD =130°.例 1. 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。求证:CE∥DF分析: 连结ABABEC是⊙O1的内接四边形ABFD是⊙O2的内接四边形∠E+∠CAB=180°,∠CAB=∠F∠E+∠F=180°CE∥DF证明:连结AB∵ABEC是⊙O1的内接四边形,∴∠1=∠F∵ADFB是⊙O2的内接四边形,∴∠E+∠1=180°∴∠E+∠F=180°∴CE∥DF1例 1. 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。求证:CE∥DF.小结:圆的内接四边形的性质定理: 圆的内接四边形的对角互补,并且任何一个外角都等于它的内角的对角。问题2:如何判定一个四边形有外接圆?2.如果逆命题成立,我们可以得到四边形存在外接圆的判定定理.1.圆内接四边形的性质定理1的逆命题是什么吗? 逆命题:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。如何证明逆命题: 如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。性质定理:圆的内接四边形的对角互补.CODBA如果能够由条件得到⊙O过点D,那么就证明了命题.分析:不在同一直线上的三点确定一个圆。经过A、B、C、三点作⊙O,讨论: ⊙O与点D有几种位置关系?三种:(1)点D在圆⊙O外;(2)点D在圆⊙O内;(3)点D在圆⊙O上.如果我们否定了点D在圆⊙O外和点D在圆⊙O内;则点D在圆⊙O上成立;如何否定了点D在圆⊙O外和点D在圆⊙O内?采用反证法把点D在圆⊙O外和点D在圆⊙O内情况一一否定。已知:在四边形ABCD中,∠B+∠D=180°,求证:A,B,C,D四点在同一个圆周上(简称四点共圆).CODBA反证法证明:(1)假设点D在圆⊙O外;E设E是AD与圆周的交点,连接EC,则有∠AEC+∠B=180°.由题设∠B+∠D=180°.可得∠D=∠AEC.这与“三角形的外角大于任意不相邻的内角”矛盾.故D点不可能在圆外.反证法证明:(2)假设点D在圆⊙O内;CODBA显然AD的延长线必与圆相交,设交点为E,连接CE,则有∠B+∠E =180°.∵∠B+∠D=180°.∴∠E=∠ADC.这与“三角形的外角大于任意不相邻的内角”矛盾.∴D点不可能在圆内.综上所述,点D只能在圆周上,即A、B、C、D四点共圆.定理: 如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。圆内接四边形的判定定理:回顾: 在圆内接四边形判定定理的证明中,我们用分类思想对点D与A、B、C三点确定的圆的位置关系进行了讨论,在每一种情形中都运用了反证法进行了证明.穷举法: 当问题的结论存在多种情形时,通过对每一种情形分别论证,最后获证结论的方法,称为穷举法.这种证明问题的方法叫穷举法.圆内接四边形的判定定理的推论:推论: 如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆。(如何证明?)证明:∵∠BCD+∠DCE=180°,又∵∠A=∠DCE,∴∠BCD+∠A=180°,∴A、B、 C、D四点共圆.圆内接四边形的判定定理:定理: 如果一个四边形的对角互补,或一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.例2.如图,CF是△ABC的AB边上的高,FP⊥BC, FQ⊥AC.求证:A、B、P、Q四点共圆.CABQPF分析:只需说明A、B、P、Q四点确定的四边形的对角互补或外角等于内对角,因此需连接QP.证明:连接QP.在四边形QFPC中,∵ FP⊥BC , FQ⊥AC,∴∠FQA=∠FPC,∴ Q、F、P、C四点共圆.∴∠QFC=∠QPC,又∵CF⊥AB ,∴∠QFC与∠QFA互余.而∠A与∠QFA也互余.∴∠A=∠QFC,∴∠A=∠QPC,∴A、B、P、Q四点共圆.小结:圆内接四边形的性质与判定定理.1.性质定理:2.判定定理:课后作业:课本P30习题2.2:1,2,3. 圆的内接四边形的对角互补,并且任何一个外角都等于它的内角的对角。 如果一个四边形的对角互补,或一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.再见!再见!再见!再见!再见!再见!再见!再见!二圆内接四边形的 性质和判定定理补充习题补充2.如图,在正方形ABCD中,M为AB上一点, N为BC上一点,且BM=BN,BP⊥MC于点P,求证:(1)△BPN∽△CPD;(2)DP⊥NP.分析(1):欲证△BPN∽△CPD;而∠DCP=∠BMC =∠CBP(为什么?)又Rt△MPB∽Rt△BPC;又BM=BN,BC=DC;故△BPN∽△CPD成立;分析(2):欲证DP⊥NP.需证∠DPN= ∠DPC+ ∠NPC=90°;由(1)知∠DPC= ∠BPN°;而∠BPN+ ∠NPC=90°;则∠DPN= ∠DPC+ ∠NPC=90°成立;即DP⊥NP成立. 圆内接四边形性质定理 圆内接四边形对角互补 如果一个多边形的所有顶点都在一个圆上,这个多边形就叫做圆内接多边形,这个圆就是多边形的外接圆DBAC·O 圆内接四边形判定定理 对角互补的四边形内接于圆 一个四边形内接于圆也称这个四边形的顶点四点共圆 定理 若两点在一条线段同侧且对该线段张角相等,则此两点与线段两个端点共圆 特别的,对定线段张角为直角的点共圆 例1、如图,⊙O1与⊙O2交于点M、N,直线AB过M与⊙O1与⊙O2 分别交于点A、B,直线CD过N与⊙O1与⊙O2 分别交于点C、D,求证:AC//BDDBO1·ACMN·O2 例2、如图,D为△ABC的边BC上一点,⊙O1经过点B、D,交AB于另一点E,⊙O2 经过点C、D,交AC于另一点F,⊙O1与⊙O2 交于点G,求证:(1)∠BAC+∠EGF=180°CFO1·ABGD·O2 (2)∠EAG=∠EFG E 例3、如图,以锐角三角形ABC的三边为边向外作三个等边三角形ABD、BCE、CAG,求证:△ABD、△BCE、△CAG的外接圆⊙O1 、⊙O2、⊙O3交于一点·O2A·O3CEBO1·GD
