人教版选修4-1 2.2圆内接四边形的性质与判定定理课件(20张)
文档属性
| 名称 | 人教版选修4-1 2.2圆内接四边形的性质与判定定理课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 604.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-14 00:00:00 | ||
图片预览






文档简介
课件20张PPT。2.2 圆内接四边形的性质
与判定定理圆心角的度数等于它所对的弧的度数。同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等.半 圆(或直径)所对的圆周角是直角;
90o的圆周角所对的弦是直径.圆上一条弧所对的圆周角等于它所对的
圆心角的一半。圆周角定理圆心角定理推论1推论2【温故知新】 如果多边形所有顶点都在一个圆上.那么这个多边形叫做圆的内接多边形,这个圆叫做多边形的外接圆.需要具备
什么样的
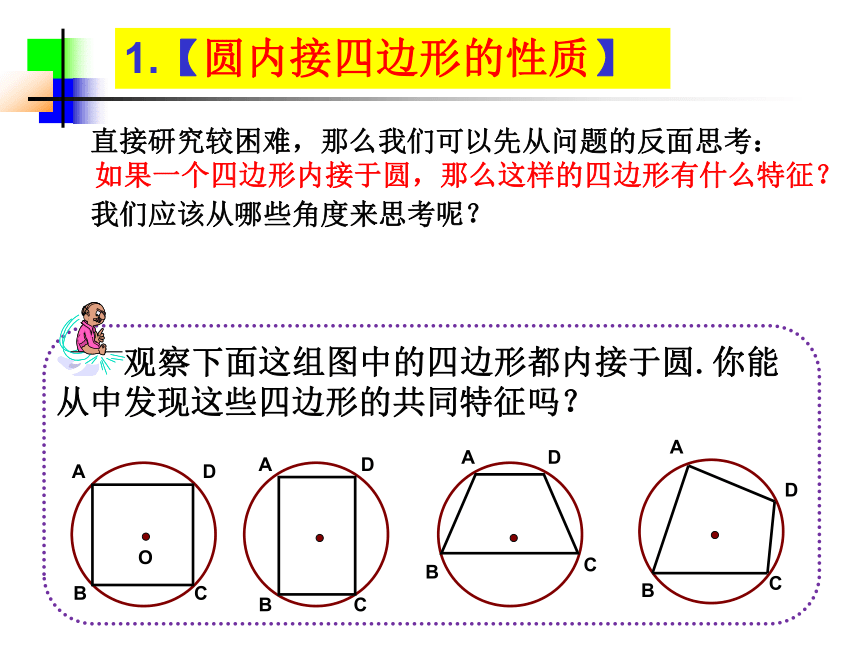
条件呢?1.【圆内接四边形的性质】 直接研究较困难,那么我们可以先从问题的反面思考:
如果一个四边形内接于圆,那么这样的四边形有什么特征?
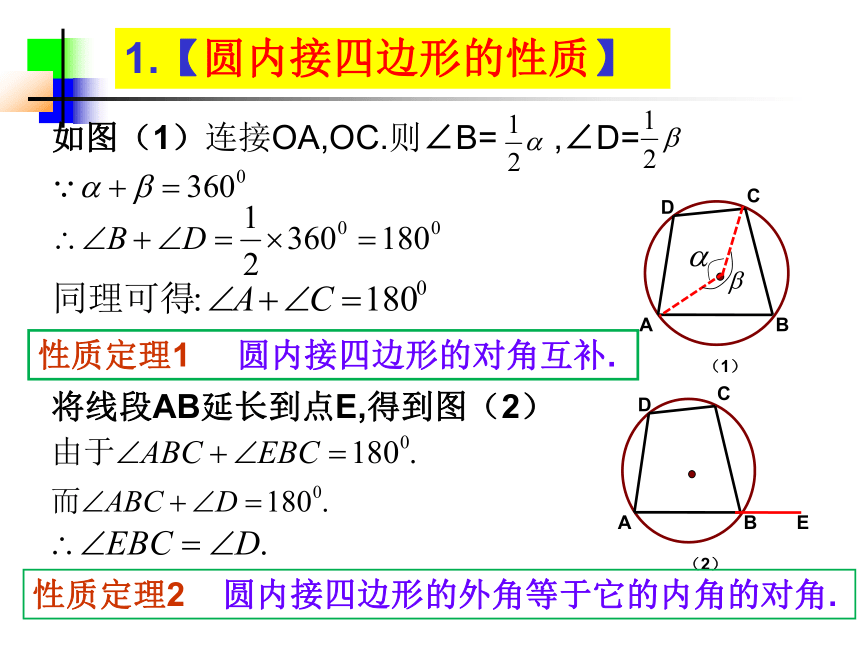
我们应该从哪些角度来思考呢?1.【圆内接四边形的性质】性质定理1 圆内接四边形的对角互补.将线段AB延长到点E,得到图(2)(1)性质定理2 圆内接四边形的外角等于它的内角的对角.1.【圆内接四边形的性质】性质定理1的逆命题:
如果一个四边形的对角互补,那么它的四个顶点共圆. 性质定理1的逆命题:
如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆. 性质定理1 圆内接四边形的对角互补性质定理2 圆内接四边形的外角等于它的内角的对角.1.【圆内接四边形的性质】假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).分析:不共线的三点确定一个圆,经过A、B、C三点可以做一个圆O,如果能由条件得出圆O过D就证明了.(1)显然,点D与圆有且只有三种位置关系:(1)点D在圆外;
(2)点D在圆内;
(3)点D在圆上;2.【圆内接四边形的判断定理】假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).证明:(1)如果点D在⊙O外部. (1)∠AEC+∠B=180°得∠AEC =∠D这与“三角形外角大于任意不相邻的内角”矛盾.故点D不可能在圆外.E因∠D+∠B=180°设E是AD与圆周 的交点,连接EC,则有点D在内部
怎么证明?2.【圆内接四边形的判断定理】假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).(2)如果点D在⊙O内部.∵∠B+∠ADC=180°
∴∠E=∠ADC综上所述,点D只能在圆周上,即A、B、C、D四点共圆.∴点D不可能在⊙O内.延长AD交圆于点E, 连接CE,则
∠B+∠E=180°这同样与“三角形外角大于任意不相邻的内角”矛盾.2.【圆内接四边形的判断定理】圆内接四边形判定定理 :
如果一个四边形的对角互补,那么它的四个顶点共圆. 当问题的结论存在多种情形时,通过对每一种情形分别论证,最后获证结论的方法---------穷举法推论 :
如果四边形的一个外角等于它的内角的对角,那么它的四个顶点共圆. 2.【圆内接四边形的判断定理】[悟一法] 判定四点共圆的方法常有:
(1)如果四个点与一定点的距离相等,那么这四个点
共圆.
(2)如果一个四边形的一组对角互补,那么这个四边
形的四个顶点共圆.
(3)如果一个四边形的一个外角等于它的内对角,那
么这个四边形的四个顶点共圆.
(4)如果两个三角形有公共边,公共边所对的角相等
且在公共边的同侧,那么这两个三角形的四个顶点共圆.思维拓展圆内接平行四边形一定是_____形
圆内接梯形一定是__________形
圆形内接菱形一定是________形 矩形等腰梯形正方形证明:连接PQ。在四边形QFPC中,∵FP⊥BC FQ⊥AC.∴∠FQA=∠FPC=90o.∴Q,F,P,C四点共圆。∴∠QFC=∠QPC.又∵CF⊥AB ∴∠QFC与∠QFA互余.而∠A与∠QFA也互余.∴∠A=∠QFC.∴∠A=∠QPC.∴A,B,P,Q四点共圆习题2.21.AD,BE是△ABC的两条高,
求证:∠CED=∠ABC.2.求证:对角线互相垂直的四边形中,各边中点在同
一个圆周上。3.如图,已知四边形ABCD内接于圆,延长AB和DC相
交于E,EG平分∠E,且与BC,AD分别相交于F,G.
求证: ∠CFG=∠DGF.性质定理1 圆内接四边形的对角互补.性质定理2 圆内接四边形的外角等于它的内角的对角.圆内接四边形判定定理 :
如果一个四边形的对角互补,那么它的四个顶点共圆. 推论 :
如果四边形的一个外角等于它的内角的对角,那么它的四个顶点共圆. 【本节收获】[悟一法] (1)圆内接四边形性质定理为几何论证中角的相等或互补提供了一个理论依据,因而也为论证角边关系提供了一种新的途径.
(2)在解有关圆内接四边形的几何问题时,既要注意性质定理的运用,也要注意判定定理的运用,又要注意两者的综合运用.(3)构造全等或相似三角形,以达到证明线段相等、角相等或线段成比例等目的. 5、如图,已知四边形是圆内接四边形,是⊙的直径,且EB⊥AD,AD与BC得延长线相交于F,
求证:证明:连结 AC, ∵∠ACB=∠DAB
∴弧AB=弧BD,∴∠ACB=∠DAB.
∵四边形ABCD是圆内接四边形,
∴∠FCD=∠DAB, ∠FDC=∠ABC. ∴ ∠ACB=∠FCD.
∴△ABC与△ABC相似.
∴即证.备选例题习题2.2(第30页)
与判定定理圆心角的度数等于它所对的弧的度数。同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等.半 圆(或直径)所对的圆周角是直角;
90o的圆周角所对的弦是直径.圆上一条弧所对的圆周角等于它所对的
圆心角的一半。圆周角定理圆心角定理推论1推论2【温故知新】 如果多边形所有顶点都在一个圆上.那么这个多边形叫做圆的内接多边形,这个圆叫做多边形的外接圆.需要具备
什么样的
条件呢?1.【圆内接四边形的性质】 直接研究较困难,那么我们可以先从问题的反面思考:
如果一个四边形内接于圆,那么这样的四边形有什么特征?
我们应该从哪些角度来思考呢?1.【圆内接四边形的性质】性质定理1 圆内接四边形的对角互补.将线段AB延长到点E,得到图(2)(1)性质定理2 圆内接四边形的外角等于它的内角的对角.1.【圆内接四边形的性质】性质定理1的逆命题:
如果一个四边形的对角互补,那么它的四个顶点共圆. 性质定理1的逆命题:
如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆. 性质定理1 圆内接四边形的对角互补性质定理2 圆内接四边形的外角等于它的内角的对角.1.【圆内接四边形的性质】假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).分析:不共线的三点确定一个圆,经过A、B、C三点可以做一个圆O,如果能由条件得出圆O过D就证明了.(1)显然,点D与圆有且只有三种位置关系:(1)点D在圆外;
(2)点D在圆内;
(3)点D在圆上;2.【圆内接四边形的判断定理】假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).证明:(1)如果点D在⊙O外部. (1)∠AEC+∠B=180°得∠AEC =∠D这与“三角形外角大于任意不相邻的内角”矛盾.故点D不可能在圆外.E因∠D+∠B=180°设E是AD与圆周 的交点,连接EC,则有点D在内部
怎么证明?2.【圆内接四边形的判断定理】假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).(2)如果点D在⊙O内部.∵∠B+∠ADC=180°
∴∠E=∠ADC综上所述,点D只能在圆周上,即A、B、C、D四点共圆.∴点D不可能在⊙O内.延长AD交圆于点E, 连接CE,则
∠B+∠E=180°这同样与“三角形外角大于任意不相邻的内角”矛盾.2.【圆内接四边形的判断定理】圆内接四边形判定定理 :
如果一个四边形的对角互补,那么它的四个顶点共圆. 当问题的结论存在多种情形时,通过对每一种情形分别论证,最后获证结论的方法---------穷举法推论 :
如果四边形的一个外角等于它的内角的对角,那么它的四个顶点共圆. 2.【圆内接四边形的判断定理】[悟一法] 判定四点共圆的方法常有:
(1)如果四个点与一定点的距离相等,那么这四个点
共圆.
(2)如果一个四边形的一组对角互补,那么这个四边
形的四个顶点共圆.
(3)如果一个四边形的一个外角等于它的内对角,那
么这个四边形的四个顶点共圆.
(4)如果两个三角形有公共边,公共边所对的角相等
且在公共边的同侧,那么这两个三角形的四个顶点共圆.思维拓展圆内接平行四边形一定是_____形
圆内接梯形一定是__________形
圆形内接菱形一定是________形 矩形等腰梯形正方形证明:连接PQ。在四边形QFPC中,∵FP⊥BC FQ⊥AC.∴∠FQA=∠FPC=90o.∴Q,F,P,C四点共圆。∴∠QFC=∠QPC.又∵CF⊥AB ∴∠QFC与∠QFA互余.而∠A与∠QFA也互余.∴∠A=∠QFC.∴∠A=∠QPC.∴A,B,P,Q四点共圆习题2.21.AD,BE是△ABC的两条高,
求证:∠CED=∠ABC.2.求证:对角线互相垂直的四边形中,各边中点在同
一个圆周上。3.如图,已知四边形ABCD内接于圆,延长AB和DC相
交于E,EG平分∠E,且与BC,AD分别相交于F,G.
求证: ∠CFG=∠DGF.性质定理1 圆内接四边形的对角互补.性质定理2 圆内接四边形的外角等于它的内角的对角.圆内接四边形判定定理 :
如果一个四边形的对角互补,那么它的四个顶点共圆. 推论 :
如果四边形的一个外角等于它的内角的对角,那么它的四个顶点共圆. 【本节收获】[悟一法] (1)圆内接四边形性质定理为几何论证中角的相等或互补提供了一个理论依据,因而也为论证角边关系提供了一种新的途径.
(2)在解有关圆内接四边形的几何问题时,既要注意性质定理的运用,也要注意判定定理的运用,又要注意两者的综合运用.(3)构造全等或相似三角形,以达到证明线段相等、角相等或线段成比例等目的. 5、如图,已知四边形是圆内接四边形,是⊙的直径,且EB⊥AD,AD与BC得延长线相交于F,
求证:证明:连结 AC, ∵∠ACB=∠DAB
∴弧AB=弧BD,∴∠ACB=∠DAB.
∵四边形ABCD是圆内接四边形,
∴∠FCD=∠DAB, ∠FDC=∠ABC. ∴ ∠ACB=∠FCD.
∴△ABC与△ABC相似.
∴即证.备选例题习题2.2(第30页)
