人教A版高中数学必修一 2.3幂函数 教案
文档属性
| 名称 | 人教A版高中数学必修一 2.3幂函数 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 111.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-15 00:00:00 | ||
图片预览



文档简介
2.3 幂函数
(一)教学目标
1.知识与技能
(1)理解幂函数的概念,会画幂函数y=x,y=x2,y=x3,y=x-1,y=x的图象.
(2)结合这几个幂函数的图象,理解幂函数图象的变化情况和性质.
2.过程与方法
(1)通过观察、总结幂函数的性质,培养学生概括抽象和识图能力.
(2)使学生进一步体会数形结合的思想.
3. 情感、态度、价值观
(1)通过生活实例引出幂函数的概念,使学生体会到数学在实际生活中的应用,激发学生的学习兴趣.
(2)利用计算机,了解幂函数图象的变化规律,使学生认识到现代技术在数学认知过程中的作用,从而激发学生的学习欲望.
(二)教学重点、难点
重点:常见幂函数的概念、图象和性质.
难点:幂函数的单调性及比较两个幂值的大小.
(三)教学方法
采用师生互动的方式,由学生自我探索、自我分析,合作学习,充分发挥学生的积极性与主动性.
利用实物投影仪及计算机辅助教学.
教学过程
教学
环节
教学内容
师生互动
设计意图
复习
引入
(多媒体显示以下5个问题,同时附注相关图象,每个问题的结论由学生说出,然后再在多面体屏幕上弹出)
问题1:如果张红购买了每千克1元的蔬菜w千克,那么她需要付的钱数p=w元,这里p是w的函数.
问题2:如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数.
问题3:如果正方体的边长为a,那么正方体的体积V=a3,这里V是a的函数.
问题4:如果正方形场地的面积为S,那么正方形的边长a=S,这里a是S的函数.
问题5:如果某人t s内骑车行进了1 km,那么他骑车的平均速度v=t-1 km/s,这里v是t的函数.
学生阅读、思考、交流、口答,教师板演.
师:观察上述例子中函数模型,这几个函数表达式有什么共同特征?
生:解析式的右边都是指数式,且底数都是变量. 变量在底数位置,解析式右边又都是幂的形式,我们把这种函数叫做幂函数.
(引入新课,书写课题)
培养学生的观察、归纳、概括能力,
形成
概念
幂函数的定义
一般地,形如(R)的函数称为幂函数,其中是自变量,是常数.
师:请同学们举出几个具体的
幂函数.
生:如等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.
理解幂函数的定义.
深化
概念
1.研究幂函数的图像
(1)
(2)
(3)
(4)
(5)
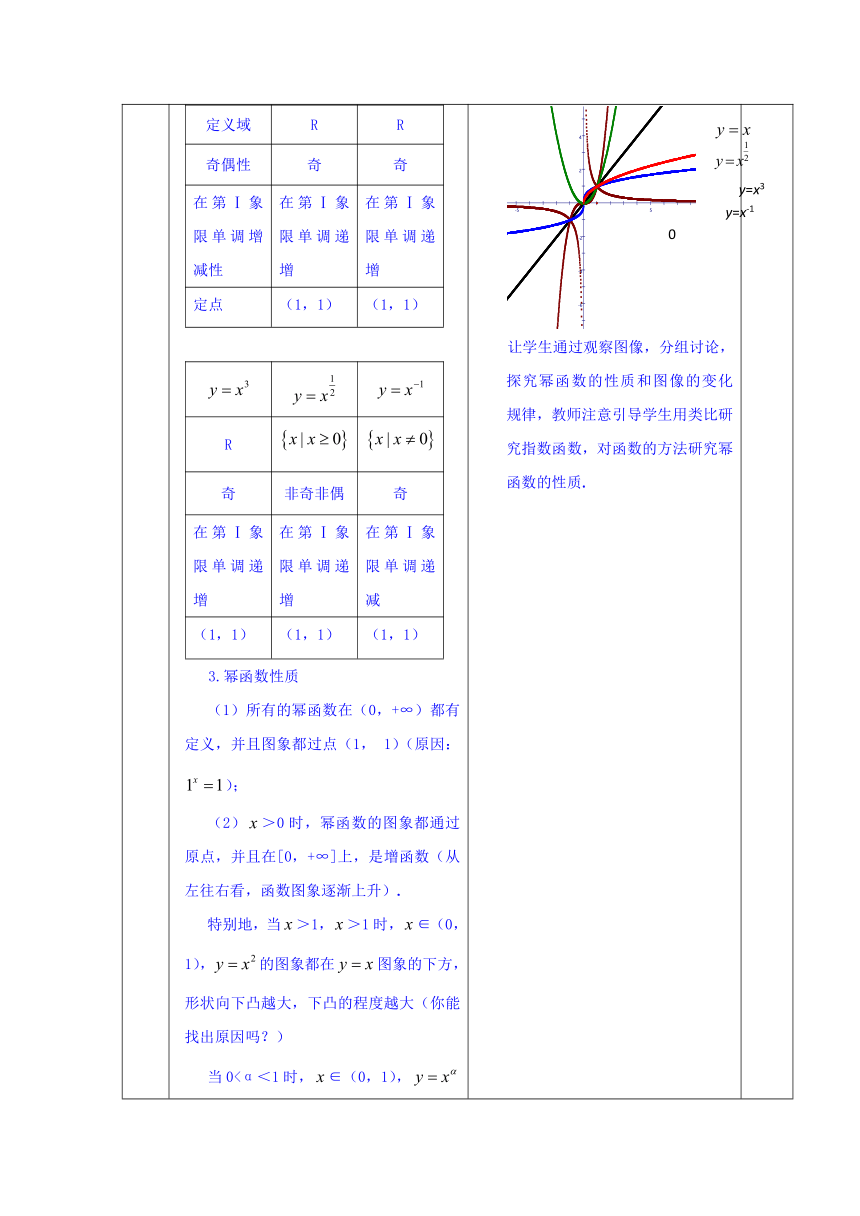
2.通过观察图像,填P86探究中的表格
定义域
R
R
奇偶性
奇
奇
在第Ⅰ象限单调增减性
在第Ⅰ象限单调递增
在第Ⅰ象限单调递增
定点
(1,1)
(1,1)
R
奇
非奇非偶
奇
在第Ⅰ象限单调递增
在第Ⅰ象限单调递增
在第Ⅰ象限单调递减
(1,1)
(1,1)
(1,1)
3.幂函数性质
(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1, 1)(原因:);
(2)>0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(从左往右看,函数图象逐渐上升).
特别地,当>1,>1时,∈(0,1),的图象都在图象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)
当0<α<1时,∈(0,1),的图象都在的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)
(3)α<0时,幂函数的图象在区间(0,+∞)上是减函数.
在第一家限内,当向原点靠近时,图象在轴的右方无限逼近轴正半轴,当慢慢地变大时,图象在轴上方并无限逼近轴的正半轴.
引导学生用列表描点法,应用函数的性质,如奇偶性,定义域等,画出函数图像,最后,教师利用电脑软件画出以上五个数数的图像.
让学生通过观察图像,分组讨论,探究幂函数的性质和图像的变化规律,教师注意引导学生用类比研究指数函数,对函数的方法研究幂函数的性质.
探究幂函数的性质和图像的变化规律,
应用
举例
例1 求下列幂函数的定义域,并指出其奇偶性、单调性.
(1)y=x;(2)y=x;(3)y=x-2.
例2 证明幂函数f(x)=在[0,+∞)上是增函数.
请同学们回顾一下如何证明一个函数是增函数,然后请一个学生作答,师板书.
合作探究:
【例3】 比较下列各组数的大小:
(1)1.5,1.7,1;
(2)(-),(-),1.1;
(3)3.8,3.9,(-1.8);
(4)31.4,51.5.
课堂练习
1.下列函数中,是幂函数的是
A.y=-x B.y=3x2 C.y= D.y=2x
2.下列结论正确的是
A.幂函数的图象一定过(0,0)和
(1,1)
B.当α<0时,幂函数y=xα是减函数
C.当α>0时,幂函数y=xα是增函数
D.函数y=x2既是二次函数,也是幂函数
3.函数y=x的图象大致是
4.幂函数f(x)=ax(m∈Z)的图象与x轴和y轴均无交点,并且图象关于原点对称,求a和m.
例1分析:解决有关函数求定义域的问题时,可以从以下几个方面来考虑,列出相应不等式(组),解不等式(组)即可得到所求函数的定义域.
①若函数解析式中含有分母,分母不能为0;
②若函数解析式中含有根号,要注意偶次根号下非负;
③0的0次幂没有意义;
④若函数解析式中含有对数式,要注意对数的真数大于0.
解:(1)函数y=x,即y=,其定义域为R,是偶函数,它在[0,+∞)上单调递增,在(-∞,0]上单调递减.
(2)函数y=x,即y=,其定义域为(0,+∞),它既不是奇函数,也不是偶函数,它在(0,+∞)上单调递减.
(3)函数y=x-2,即y=,其定义域为(-∞,0)∪(0,+∞),是偶函数.它在区间(-∞,0)和(0,+∞)上都单调递减.
例2证明:设0≤x1<x2,
则f(x1)-f(x2)
=-
=
=,
因为x1-x2<0,
+>0,
所以f(x1)<f(x2),
即幂函数f(x)=在
[0,+∞)上是增函数.
小结:以上是用作差法证明函数的单调性,还可以用作商法证明函数的单调性,作简要分析,提出注意点:在证得<1后,要比较f(x1)与f(x2)的大小,要注意分母的符号.
例3分析:比较两个或多个数值的大小,一般情况下是将所要比较的两个或多个数值转化为比较某一函数的不同函数值的大小问题,进而根据所确定的函数的单调性,比较自变量的大小即可.若所给的数值不能转化为比较同一函数的不同函数值的大小问题,可以找出中间量来作为桥梁间接地进行比较,确定出它们的大小关系,一般情况下是根据具体情况选择常数“1”“-1”或“0”这些数作为中间量来进行比较.
解:(1)∵所给的三个数之中1.5和1.7的指数相同,且1的任何次幂都是1,因此,比较幂1.5、1.7、1的大小就是比较1.5、1.7、1的大小,也就是比较函数y=x中,当自变量分别取1.5、1.7和1时对应函数值的大小关系,因为自变量的值的大小关系容易确定,只需确定函数y=x的单调性即可,又函数y=x在(0,+∞)上单调递增,且1.7>1.5>1,所以1.7>1.5>1.
(2)(-)=(),
(-)=(),
1.1=[(1.1)2]=1.21.
∵幂函数y=x在(0,+∞)上单调递减,且<<1.21,
∴()>()
>1.21,
即(-)>(-)
>1.1.
(3)利用幂函数和指数函数的单调性可以发现0<3.8<1,3.9>1,(-1.8)<0,从而可以比较出它们的大小.
(4)它们的底和指数也都不同,而且都大于1,我们插入一个中间数31.5,利用幂函数和指数函数的单调性可以发现31.4<31.5<51.5.
小结:(1)当底数相异,指数相同的数比较大小,可以转化为比较同一幂函数的不同函数值的大小问题,根据函数的单调性,只要比较自变量的大小就可以了.
(2)当底和指数都不同,插入一个中间数,综合利用幂函数和指数函数的单调性来比较.
课堂练习答案:
1. C 2. D
3. D 4. a=1,m=1,3,5,7.
掌握幂函数知识的应用.
归纳
总结
1.幂函数的概念以及它和指数函数表达式的区别.
2.常见幂函数的图象和性质.
3.幂值的大小比较方法.
学生先自回顾反思,教师点评完善.
形成知识体系.
课后
作业
作业:2.3 第一课时 习案
学生独立完成
巩固新知
提升能力
备选例题
例1 已知是幂函数,求m,n的值.
【解析】由题意得,
解得, 所以.
【小结】做本题时,常常忽视m2 + 2m – 2 = 1且2n – 3 = 0这些条件.
表达式y =(x∈R)的要求比较严格,系数为1,底数是x,∈R为常数,如,y = 1 = x0为幂函数,而如y = 2x2,y = (x – 1)3等都不是幂函数.
例2 比例下列各组数的大小.
(1);
(2)(–2)–3和(–2.5)–3;
(3)(1.1)–0.1和(1.2)–0.1;
(4).
【解析】(1),函数在
(0, +∞)上为增函数,又,则,
从而.
(2)幂函数y = x–3在(–∞, 0)和(0, +∞)上为减函数,
又∵–2>–2.5,∴(–2)–3<(–2.5)–3.
(3)幂函数y = x–0.1在(0, +∞)上为减函数,
又∵1.1<1.2,∴1.1–0.1>1.2–0.1.
(4)>= 1;0<<= 1;
<0,
∴<<.
【小结】比较大小题,要综合考虑函数的性质,特别是单调性的应用,更善于用“搭桥”法进行分组,常数0和1是常用的“桥梁”.
(一)教学目标
1.知识与技能
(1)理解幂函数的概念,会画幂函数y=x,y=x2,y=x3,y=x-1,y=x的图象.
(2)结合这几个幂函数的图象,理解幂函数图象的变化情况和性质.
2.过程与方法
(1)通过观察、总结幂函数的性质,培养学生概括抽象和识图能力.
(2)使学生进一步体会数形结合的思想.
3. 情感、态度、价值观
(1)通过生活实例引出幂函数的概念,使学生体会到数学在实际生活中的应用,激发学生的学习兴趣.
(2)利用计算机,了解幂函数图象的变化规律,使学生认识到现代技术在数学认知过程中的作用,从而激发学生的学习欲望.
(二)教学重点、难点
重点:常见幂函数的概念、图象和性质.
难点:幂函数的单调性及比较两个幂值的大小.
(三)教学方法
采用师生互动的方式,由学生自我探索、自我分析,合作学习,充分发挥学生的积极性与主动性.
利用实物投影仪及计算机辅助教学.
教学过程
教学
环节
教学内容
师生互动
设计意图
复习
引入
(多媒体显示以下5个问题,同时附注相关图象,每个问题的结论由学生说出,然后再在多面体屏幕上弹出)
问题1:如果张红购买了每千克1元的蔬菜w千克,那么她需要付的钱数p=w元,这里p是w的函数.
问题2:如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数.
问题3:如果正方体的边长为a,那么正方体的体积V=a3,这里V是a的函数.
问题4:如果正方形场地的面积为S,那么正方形的边长a=S,这里a是S的函数.
问题5:如果某人t s内骑车行进了1 km,那么他骑车的平均速度v=t-1 km/s,这里v是t的函数.
学生阅读、思考、交流、口答,教师板演.
师:观察上述例子中函数模型,这几个函数表达式有什么共同特征?
生:解析式的右边都是指数式,且底数都是变量. 变量在底数位置,解析式右边又都是幂的形式,我们把这种函数叫做幂函数.
(引入新课,书写课题)
培养学生的观察、归纳、概括能力,
形成
概念
幂函数的定义
一般地,形如(R)的函数称为幂函数,其中是自变量,是常数.
师:请同学们举出几个具体的
幂函数.
生:如等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.
理解幂函数的定义.
深化
概念
1.研究幂函数的图像
(1)
(2)
(3)
(4)
(5)
2.通过观察图像,填P86探究中的表格
定义域
R
R
奇偶性
奇
奇
在第Ⅰ象限单调增减性
在第Ⅰ象限单调递增
在第Ⅰ象限单调递增
定点
(1,1)
(1,1)
R
奇
非奇非偶
奇
在第Ⅰ象限单调递增
在第Ⅰ象限单调递增
在第Ⅰ象限单调递减
(1,1)
(1,1)
(1,1)
3.幂函数性质
(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1, 1)(原因:);
(2)>0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(从左往右看,函数图象逐渐上升).
特别地,当>1,>1时,∈(0,1),的图象都在图象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)
当0<α<1时,∈(0,1),的图象都在的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)
(3)α<0时,幂函数的图象在区间(0,+∞)上是减函数.
在第一家限内,当向原点靠近时,图象在轴的右方无限逼近轴正半轴,当慢慢地变大时,图象在轴上方并无限逼近轴的正半轴.
引导学生用列表描点法,应用函数的性质,如奇偶性,定义域等,画出函数图像,最后,教师利用电脑软件画出以上五个数数的图像.
让学生通过观察图像,分组讨论,探究幂函数的性质和图像的变化规律,教师注意引导学生用类比研究指数函数,对函数的方法研究幂函数的性质.
探究幂函数的性质和图像的变化规律,
应用
举例
例1 求下列幂函数的定义域,并指出其奇偶性、单调性.
(1)y=x;(2)y=x;(3)y=x-2.
例2 证明幂函数f(x)=在[0,+∞)上是增函数.
请同学们回顾一下如何证明一个函数是增函数,然后请一个学生作答,师板书.
合作探究:
【例3】 比较下列各组数的大小:
(1)1.5,1.7,1;
(2)(-),(-),1.1;
(3)3.8,3.9,(-1.8);
(4)31.4,51.5.
课堂练习
1.下列函数中,是幂函数的是
A.y=-x B.y=3x2 C.y= D.y=2x
2.下列结论正确的是
A.幂函数的图象一定过(0,0)和
(1,1)
B.当α<0时,幂函数y=xα是减函数
C.当α>0时,幂函数y=xα是增函数
D.函数y=x2既是二次函数,也是幂函数
3.函数y=x的图象大致是
4.幂函数f(x)=ax(m∈Z)的图象与x轴和y轴均无交点,并且图象关于原点对称,求a和m.
例1分析:解决有关函数求定义域的问题时,可以从以下几个方面来考虑,列出相应不等式(组),解不等式(组)即可得到所求函数的定义域.
①若函数解析式中含有分母,分母不能为0;
②若函数解析式中含有根号,要注意偶次根号下非负;
③0的0次幂没有意义;
④若函数解析式中含有对数式,要注意对数的真数大于0.
解:(1)函数y=x,即y=,其定义域为R,是偶函数,它在[0,+∞)上单调递增,在(-∞,0]上单调递减.
(2)函数y=x,即y=,其定义域为(0,+∞),它既不是奇函数,也不是偶函数,它在(0,+∞)上单调递减.
(3)函数y=x-2,即y=,其定义域为(-∞,0)∪(0,+∞),是偶函数.它在区间(-∞,0)和(0,+∞)上都单调递减.
例2证明:设0≤x1<x2,
则f(x1)-f(x2)
=-
=
=,
因为x1-x2<0,
+>0,
所以f(x1)<f(x2),
即幂函数f(x)=在
[0,+∞)上是增函数.
小结:以上是用作差法证明函数的单调性,还可以用作商法证明函数的单调性,作简要分析,提出注意点:在证得<1后,要比较f(x1)与f(x2)的大小,要注意分母的符号.
例3分析:比较两个或多个数值的大小,一般情况下是将所要比较的两个或多个数值转化为比较某一函数的不同函数值的大小问题,进而根据所确定的函数的单调性,比较自变量的大小即可.若所给的数值不能转化为比较同一函数的不同函数值的大小问题,可以找出中间量来作为桥梁间接地进行比较,确定出它们的大小关系,一般情况下是根据具体情况选择常数“1”“-1”或“0”这些数作为中间量来进行比较.
解:(1)∵所给的三个数之中1.5和1.7的指数相同,且1的任何次幂都是1,因此,比较幂1.5、1.7、1的大小就是比较1.5、1.7、1的大小,也就是比较函数y=x中,当自变量分别取1.5、1.7和1时对应函数值的大小关系,因为自变量的值的大小关系容易确定,只需确定函数y=x的单调性即可,又函数y=x在(0,+∞)上单调递增,且1.7>1.5>1,所以1.7>1.5>1.
(2)(-)=(),
(-)=(),
1.1=[(1.1)2]=1.21.
∵幂函数y=x在(0,+∞)上单调递减,且<<1.21,
∴()>()
>1.21,
即(-)>(-)
>1.1.
(3)利用幂函数和指数函数的单调性可以发现0<3.8<1,3.9>1,(-1.8)<0,从而可以比较出它们的大小.
(4)它们的底和指数也都不同,而且都大于1,我们插入一个中间数31.5,利用幂函数和指数函数的单调性可以发现31.4<31.5<51.5.
小结:(1)当底数相异,指数相同的数比较大小,可以转化为比较同一幂函数的不同函数值的大小问题,根据函数的单调性,只要比较自变量的大小就可以了.
(2)当底和指数都不同,插入一个中间数,综合利用幂函数和指数函数的单调性来比较.
课堂练习答案:
1. C 2. D
3. D 4. a=1,m=1,3,5,7.
掌握幂函数知识的应用.
归纳
总结
1.幂函数的概念以及它和指数函数表达式的区别.
2.常见幂函数的图象和性质.
3.幂值的大小比较方法.
学生先自回顾反思,教师点评完善.
形成知识体系.
课后
作业
作业:2.3 第一课时 习案
学生独立完成
巩固新知
提升能力
备选例题
例1 已知是幂函数,求m,n的值.
【解析】由题意得,
解得, 所以.
【小结】做本题时,常常忽视m2 + 2m – 2 = 1且2n – 3 = 0这些条件.
表达式y =(x∈R)的要求比较严格,系数为1,底数是x,∈R为常数,如,y = 1 = x0为幂函数,而如y = 2x2,y = (x – 1)3等都不是幂函数.
例2 比例下列各组数的大小.
(1);
(2)(–2)–3和(–2.5)–3;
(3)(1.1)–0.1和(1.2)–0.1;
(4).
【解析】(1),函数在
(0, +∞)上为增函数,又,则,
从而.
(2)幂函数y = x–3在(–∞, 0)和(0, +∞)上为减函数,
又∵–2>–2.5,∴(–2)–3<(–2.5)–3.
(3)幂函数y = x–0.1在(0, +∞)上为减函数,
又∵1.1<1.2,∴1.1–0.1>1.2–0.1.
(4)>= 1;0<<= 1;
<0,
∴<<.
【小结】比较大小题,要综合考虑函数的性质,特别是单调性的应用,更善于用“搭桥”法进行分组,常数0和1是常用的“桥梁”.
