湘教版八年级数学上册 4.2 不等式的基本性质教学课件(共33张PPT)
文档属性
| 名称 | 湘教版八年级数学上册 4.2 不等式的基本性质教学课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-15 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
不等式的基本性质
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
小刚的爸爸今年32岁,小刚今年9岁,小刚说:“再过25年,我就比爸爸年龄大了”.小刚的说法对吗?
解析:肯定是不对的,再过25年,小刚在长大,爸爸也在变老了。
那么,今天我们就来探究一下小刚的错误出现在哪里,让我们开始对不等式的性质进行探究吧!
02 新知探究
新知探究
不等式的性质 1
1.用不等号填空:
(1)5 3 ;
5+2 3+2 ;
5-2 3-2 .
>
>
>
(2)2 4 ;
2+1 4+1 ;
2-3 4-3 .
<
<
<
新知探究
不等式的性质1
2. 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果.
请用“>”或“<”填空:
100 -a 84 -a
100 –a+b 84 –a+b
>
>
思考:你发现什么规律了吗?
新知探究
不等式的性质 1
不等式性质1:不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c.
用“>”或“<”填空:
已知 a>b,则a+3 b+3
解: 因为 a>b,两边都加上3,
由不等式基本性质1,得
a+3 > b+3;
>
新知探究
练一练
1.用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
根据____________.
>
不等式性质1
<
不等式性质1
新知探究
移项
由3x < 2x -2可以看出,运用不等式基本性质1 对 3x < 2x-2 进行化简的过程,就是对不等式3x< 2x-2 作了变形:
把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
即: 3x< 2x-2 3x-2x< -2
新知探究
练一练
2.下列变形中,正确的是( )
A. 由 3x -1< 2x - 2,得 x < -1
B. 由 2x +1>3x -1 ,得 x > -2
C. 由 2x + 1> x -1 ,得 x > 2
D. 由 x +2 < 2x - 2,得 x < 0
A
正解:x < 2
正解:x > -2
正解:x > 4
总结:移项只改变移动的项的符号,整个不等式的符号保持不变.
新知探究
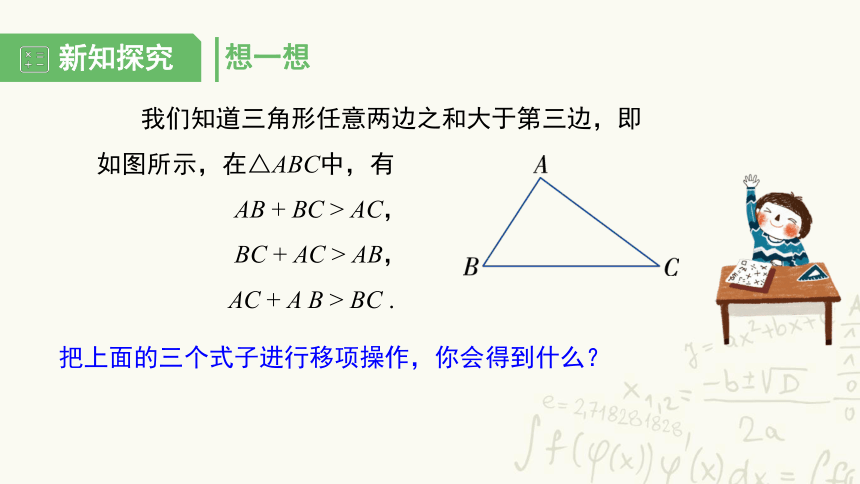
想一想
我们知道三角形任意两边之和大于第三边,即如图所示,在△ABC中,有
AB + BC > AC,
BC + AC > AB,
AC + A B > BC .
把上面的三个式子进行移项操作,你会得到什么?
新知探究
想一想
由不等式的变形,三角形的两边之差与第三边有何关系?
三角形任意两边的差小于第三边
新知探究
不等式的性质2
不等式基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a > b,c > 0,那么 ac > bc , > .
新知探究
不等式的基本性质3
不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc , < .
新知探究
练一练
3. 用“>”或“<”填空:
(1)已知 a>b,则3a 3b ;
解:因为 a>b,两边都乘3,
由不等式基本性质2,得
3a > 3b.
>
(2)已知 a>b,则-a -b .
解:因为 a>b,两边都乘-1,
由不等式基本性质3,得
-a < -b.
<
新知探究
判断正误:
(1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.
当c≤0时,不成立.
×
×
当c=0时,不成立.
√
思考: 不等式的基本性质与等式的基本性质有什么相同点和不同点?
想一想
新知探究
想一想
思考:等式有对称性及传递性,那么不等式具有对称性和传递性吗?
已知x>5,那么5性质4(对称性):如果a>b,那么b由8如:8<10,10<15 ,8 15.
<
性质5(同向传递性):如果a>b,b>c,那么a>c.
新知探究
练一练
4. 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
a<-1
03 典型例题
例题讲解
1. 把下列不等式化为x >a或x< a的形式:
(1)x + 6 > 5 ;
(2) 3x < 2x -2 .
解:
(1) x + 6 > 5,
不等式的两边都减去6,由不等式基本性质1,得
x +6-6 > 5-6,
即 x > -1.
(2) 3x < 2x -2,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-2-2x,
即 x < -2.
例题讲解
2. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b -10 a -10 .
<
>
3. 把下列不等式化为x>a或x(1)5>3+x;
解:x < 2
(2)2x<x+6.
解:x < 6
例题讲解
4. 已知a > b,用“>”或“<”填空:
(1)2a 2b ;
(2)-3a -3b ;
(3) .
>
<
<
5. 用“>”或“<”填空:
(1) 如果1-x>3,那么-x 3-1,得x -2;
(2) 如果x+2<3x+8,那么x-3x 8-2,
即-2x 6,得x -3;
>
<
<
<
>
例题讲解
6.把下列不等式化成“x>a”或“x<a”的形式.
(1)2x-2<0;
(2)3x-9<6x;
(3) x-2 > x-5.
解:(1)根据不等式的基本性质1,
两边都加上2得:2x<2.
根据不等式的基本性质2,
两边除以2得:x<1;
例题讲解
解:(2)根据不等式的基本性质1,
两边都加上9-6x得:-3x<9.
根据不等式的基本性质3,
两边都除以-3得:x>-3;
(2)3x-9<6x;
(3) x-2> x-5.
解:(3)根据不等式的基本性质1,
两边都加上2- x得:-x>-3.
根据不等式的基本性质3,
两边都除以-1得:x<3.
04 拓展提高
拓展提高
已知三角形△ABC,AB=3,AC=8,BC长为奇数,求BC的长.
分析:根据三角形三边关系定理得到第三边的范围,再根据BC为奇数和取值范围确定BC长即可.
解:根据三角形的三边关系可得8-3<BC<8+3,
即5<BC<11.
∵BC为奇数,
∴BC的长为7或9.
05 课堂小结
课堂小结
不等式的基本性质1
→
移项
→
应用
↓
三角形中,两边之差小于第三边
如果a>b,那么a+c>b+c,a-c>b-c
↓
(表达形式)
课堂小结
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
如果 那么
→
如果 那么
应用
06 作业布置
1.完成课本习题 4.2 A、B组
2.巩固今日所学,牢记心中不等式的性质
作业布置
谢 谢 观 看
不等式的基本性质
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
小刚的爸爸今年32岁,小刚今年9岁,小刚说:“再过25年,我就比爸爸年龄大了”.小刚的说法对吗?
解析:肯定是不对的,再过25年,小刚在长大,爸爸也在变老了。
那么,今天我们就来探究一下小刚的错误出现在哪里,让我们开始对不等式的性质进行探究吧!
02 新知探究
新知探究
不等式的性质 1
1.用不等号填空:
(1)5 3 ;
5+2 3+2 ;
5-2 3-2 .
>
>
>
(2)2 4 ;
2+1 4+1 ;
2-3 4-3 .
<
<
<
新知探究
不等式的性质1
2. 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果.
请用“>”或“<”填空:
100 -a 84 -a
100 –a+b 84 –a+b
>
>
思考:你发现什么规律了吗?
新知探究
不等式的性质 1
不等式性质1:不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c.
用“>”或“<”填空:
已知 a>b,则a+3 b+3
解: 因为 a>b,两边都加上3,
由不等式基本性质1,得
a+3 > b+3;
>
新知探究
练一练
1.用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
根据____________.
>
不等式性质1
<
不等式性质1
新知探究
移项
由3x < 2x -2可以看出,运用不等式基本性质1 对 3x < 2x-2 进行化简的过程,就是对不等式3x< 2x-2 作了变形:
把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
即: 3x< 2x-2 3x-2x< -2
新知探究
练一练
2.下列变形中,正确的是( )
A. 由 3x -1< 2x - 2,得 x < -1
B. 由 2x +1>3x -1 ,得 x > -2
C. 由 2x + 1> x -1 ,得 x > 2
D. 由 x +2 < 2x - 2,得 x < 0
A
正解:x < 2
正解:x > -2
正解:x > 4
总结:移项只改变移动的项的符号,整个不等式的符号保持不变.
新知探究
想一想
我们知道三角形任意两边之和大于第三边,即如图所示,在△ABC中,有
AB + BC > AC,
BC + AC > AB,
AC + A B > BC .
把上面的三个式子进行移项操作,你会得到什么?
新知探究
想一想
由不等式的变形,三角形的两边之差与第三边有何关系?
三角形任意两边的差小于第三边
新知探究
不等式的性质2
不等式基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a > b,c > 0,那么 ac > bc , > .
新知探究
不等式的基本性质3
不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc , < .
新知探究
练一练
3. 用“>”或“<”填空:
(1)已知 a>b,则3a 3b ;
解:因为 a>b,两边都乘3,
由不等式基本性质2,得
3a > 3b.
>
(2)已知 a>b,则-a -b .
解:因为 a>b,两边都乘-1,
由不等式基本性质3,得
-a < -b.
<
新知探究
判断正误:
(1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.
当c≤0时,不成立.
×
×
当c=0时,不成立.
√
思考: 不等式的基本性质与等式的基本性质有什么相同点和不同点?
想一想
新知探究
想一想
思考:等式有对称性及传递性,那么不等式具有对称性和传递性吗?
已知x>5,那么5
<
性质5(同向传递性):如果a>b,b>c,那么a>c.
新知探究
练一练
4. 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
a<-1
03 典型例题
例题讲解
1. 把下列不等式化为x >a或x< a的形式:
(1)x + 6 > 5 ;
(2) 3x < 2x -2 .
解:
(1) x + 6 > 5,
不等式的两边都减去6,由不等式基本性质1,得
x +6-6 > 5-6,
即 x > -1.
(2) 3x < 2x -2,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-2-2x,
即 x < -2.
例题讲解
2. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b -10 a -10 .
<
>
3. 把下列不等式化为x>a或x
解:x < 2
(2)2x<x+6.
解:x < 6
例题讲解
4. 已知a > b,用“>”或“<”填空:
(1)2a 2b ;
(2)-3a -3b ;
(3) .
>
<
<
5. 用“>”或“<”填空:
(1) 如果1-x>3,那么-x 3-1,得x -2;
(2) 如果x+2<3x+8,那么x-3x 8-2,
即-2x 6,得x -3;
>
<
<
<
>
例题讲解
6.把下列不等式化成“x>a”或“x<a”的形式.
(1)2x-2<0;
(2)3x-9<6x;
(3) x-2 > x-5.
解:(1)根据不等式的基本性质1,
两边都加上2得:2x<2.
根据不等式的基本性质2,
两边除以2得:x<1;
例题讲解
解:(2)根据不等式的基本性质1,
两边都加上9-6x得:-3x<9.
根据不等式的基本性质3,
两边都除以-3得:x>-3;
(2)3x-9<6x;
(3) x-2> x-5.
解:(3)根据不等式的基本性质1,
两边都加上2- x得:-x>-3.
根据不等式的基本性质3,
两边都除以-1得:x<3.
04 拓展提高
拓展提高
已知三角形△ABC,AB=3,AC=8,BC长为奇数,求BC的长.
分析:根据三角形三边关系定理得到第三边的范围,再根据BC为奇数和取值范围确定BC长即可.
解:根据三角形的三边关系可得8-3<BC<8+3,
即5<BC<11.
∵BC为奇数,
∴BC的长为7或9.
05 课堂小结
课堂小结
不等式的基本性质1
→
移项
→
应用
↓
三角形中,两边之差小于第三边
如果a>b,那么a+c>b+c,a-c>b-c
↓
(表达形式)
课堂小结
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
如果 那么
→
如果 那么
应用
06 作业布置
1.完成课本习题 4.2 A、B组
2.巩固今日所学,牢记心中不等式的性质
作业布置
谢 谢 观 看
同课章节目录
