湘教版八年级数学上册第4章 一元一次不等式(组)4.3 一元一次不等式的解法教学课件(共34张PPT)
文档属性
| 名称 | 湘教版八年级数学上册第4章 一元一次不等式(组)4.3 一元一次不等式的解法教学课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-15 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
一元一次不等式的解法
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
为了共建校园文化活动,我们班需要准备一些三角形的道具,现在有两根木条a和b,a长10cm,b长3cm,如果再找一根木条c,用这三根木条钉成一个三角形木框,那么对第三根木条c有什么要求呢?
a
b
c=?
新课导入
解:设第三根木条长度为xcm,
则由“三角形两边之和大于第三边”得:
x<10+3 ,
又由“两边之差小于第三边”得:
x>10-3
得:7
同学们是如何想到如何来求第三根木条的长度的呢?又该如何求解呢?
02 新知探究
新知探究
一元一次不等式的概念
像75+25x<1200这样,含有一个未知数,且含未知数的项的次数是1的不等式,称为一元一次不等式.
它与一元一次方程的定义有什么共同点吗?
新知探究
练一练
1.下列不等式中,哪些是一元一次不等式?
(1) 3x+2>x–1 (2) 5x+3<0
(3) (4) x(x–1)<2x
?
?
?
?
左边不是整式
化简后是
x2-x<2x
新知探究
不等式解集的概念
把满足一个不等式的未知数的每一个值,称为这个不等式的一个解.
把一个不等式的解的全体称为这个不等式的解集.
不等式的解集必须满足两个条件:
1.解集中的任何一个数值都使不等式成立;
2.解集外的任何一个数值都不能使不等式成立.
求一个不等式的解集的过程称为解不等式.
新知探究
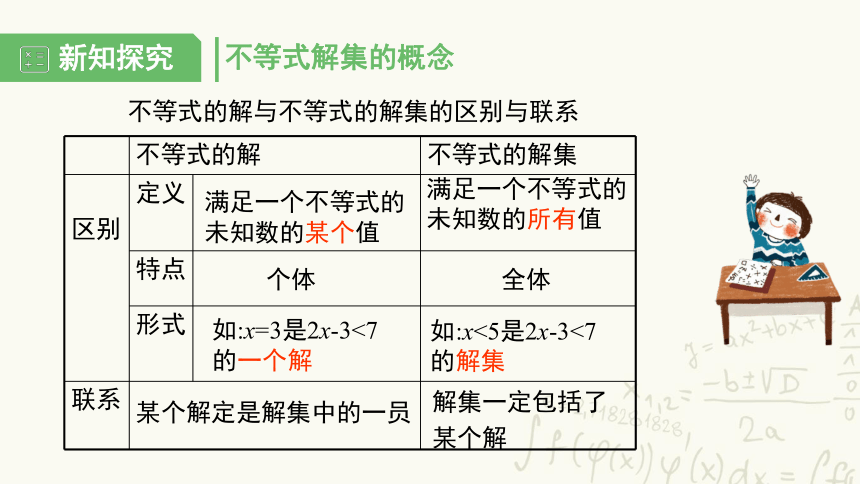
不等式解集的概念
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了
某个解
新知探究
练一练
2. 判断下列说法是否正确?
(1) x=2是不等式x+3<4的解; ( )
(2) 不等式x+1<2的解有无穷多个; ( )
(3) x=3是不等式3x<9的解 ( )
(4) x=2是不等式3x<7的解集; ( )
×
√
×
×
新知探究
小归纳
判断一个数是不是不等式的解,只要把这个数代入不等式,看是否成立.判断一个不等式的解集是否正确,可把这个不等式化为“x>a”或“x<a”的形式,再进行比较即可.
新知探究
解一元一次不等式
解不等式:
4x-1<5x+15
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
新知探究
小归纳
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
新知探究
练一练
3. 已知不等式 x+8>4x+m (m是常数)的解集是 x<3,求 m.
解:因为 x+8>4x+m,
所以 x-4x>m-8, 即-3x>m-8,
因为其解集为x<3,
所以解得 m=-1.
方法总结:已知解集求字母系数的值,通常是先解含有字母的不等式,再利用解集唯一性列方程求字母的值.解题过程体现了方程思想.
新知探究
在数轴上表示不等式的解集
如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
新知探究
练一练
4. 利用数轴来表示下列不等式的解集.
(1) x>-1 (2) x<
-1
0
0
1
用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
>、< 画空心圆.
新知探究
小归纳
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点表示;不包含在解集中,则用空心点表示.
(3)定方向:相对于边界点,大于向右画,小于向左画.
新知探究
小归纳
在数轴上表示不等式的解集时,一要把点找准确,二要找准方向,三要区别实心圆点与空心圆圈.
求不等式的特殊解,先要准确求出不等式的解集,然后确定特殊解.在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
03 典型例题
例题讲解
1. 不等式x>-2与x ≥-2的解集有什么不同?在数轴上表示它们时怎样区别?分别在数轴上把这两个解集表示出来.
例题讲解
2. 已知 是关于x的一元一次不等式,
则a的值是________.
解析:由 是关于x的一元一次不等式得2a-1=1,计算即可求出a的值等于1.
1
例题讲解
3. 下列说法:①x=0是2x-1<0的一个解;②x=-3不是3x-2>0的解;③-2x+1<0的解集是x>2.其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
解析:①x=0时,2x-1<0成立,所以x=0是2x-1<0的一个解;②x=-3时,3x-2>0不成立,所以x=-3不是3x-2>0的解;③-2x+1<0的解集是x> ,所以不正确.
C
例题讲解
4. 解不等式 12-6x≥2(1-2x),并把它的解集在数轴上表示出来.
解:去括号,得 12 -6x ≥ 2-4x
移项,得 -6x+4x ≥ 2-12
合并同类项,得 -2x ≥ -10
两边都除以-2,得 x ≤ 5
原不等式的解集在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
注意:x≤5中包含5,所以在数轴上将表示5的点画成实心圆点.
首先将括号去掉
将同类项放在一起
根据不等式基本性质2
例题讲解
5. 当x取什么值时,代数式 x +2的值大于或等于0?并求出所有满足条件的正整数.
解:根据题意,得 x +2≥ 0,
解得 x ≤ 6.
所以,当x≤6时,代数式 x+2的值大于或等于0.
x≤6在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
由图可知,满足条件的正整数有 1,2,3,4,5,6.
04 拓展提高
拓展提高
1.已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
解:由方程的定义,把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
其中正整数解有1和2.
-1
0
1
2
3
4
5
6
拓展提高
2. y为何值时,代数式 的值不大于代数式
的值,并求出满足条件的最大整数.
解:依题意,得
去分母得:4(5y+4)≤21-8(1-y),
去括号得:20y+16≤21-8+8y,
移项得:20y-8y≤21-8-16,
合并同类项得:12y≤-3,
把y的系数化为1得:y≤
在数轴上表示如下:
由图可知,满足条件的最大整数是-1.
05 课堂小结
课堂小结
一元一次不等式的解法
一元一次不等式的解集
解一元一次不等式
→
步骤
课堂小结
应用不等式的基本性质
↑
解一元一次不等式
→
将解集在数轴上表示
找符合条件的整数解
→
不等式解集的表示
↓
06 作业布置
完成课本习题 4.3 A、B组
作业布置
谢 谢 观 看
一元一次不等式的解法
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
为了共建校园文化活动,我们班需要准备一些三角形的道具,现在有两根木条a和b,a长10cm,b长3cm,如果再找一根木条c,用这三根木条钉成一个三角形木框,那么对第三根木条c有什么要求呢?
a
b
c=?
新课导入
解:设第三根木条长度为xcm,
则由“三角形两边之和大于第三边”得:
x<10+3 ,
又由“两边之差小于第三边”得:
x>10-3
得:7
同学们是如何想到如何来求第三根木条的长度的呢?又该如何求解呢?
02 新知探究
新知探究
一元一次不等式的概念
像75+25x<1200这样,含有一个未知数,且含未知数的项的次数是1的不等式,称为一元一次不等式.
它与一元一次方程的定义有什么共同点吗?
新知探究
练一练
1.下列不等式中,哪些是一元一次不等式?
(1) 3x+2>x–1 (2) 5x+3<0
(3) (4) x(x–1)<2x
?
?
?
?
左边不是整式
化简后是
x2-x<2x
新知探究
不等式解集的概念
把满足一个不等式的未知数的每一个值,称为这个不等式的一个解.
把一个不等式的解的全体称为这个不等式的解集.
不等式的解集必须满足两个条件:
1.解集中的任何一个数值都使不等式成立;
2.解集外的任何一个数值都不能使不等式成立.
求一个不等式的解集的过程称为解不等式.
新知探究
不等式解集的概念
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了
某个解
新知探究
练一练
2. 判断下列说法是否正确?
(1) x=2是不等式x+3<4的解; ( )
(2) 不等式x+1<2的解有无穷多个; ( )
(3) x=3是不等式3x<9的解 ( )
(4) x=2是不等式3x<7的解集; ( )
×
√
×
×
新知探究
小归纳
判断一个数是不是不等式的解,只要把这个数代入不等式,看是否成立.判断一个不等式的解集是否正确,可把这个不等式化为“x>a”或“x<a”的形式,再进行比较即可.
新知探究
解一元一次不等式
解不等式:
4x-1<5x+15
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
新知探究
小归纳
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
新知探究
练一练
3. 已知不等式 x+8>4x+m (m是常数)的解集是 x<3,求 m.
解:因为 x+8>4x+m,
所以 x-4x>m-8, 即-3x>m-8,
因为其解集为x<3,
所以解得 m=-1.
方法总结:已知解集求字母系数的值,通常是先解含有字母的不等式,再利用解集唯一性列方程求字母的值.解题过程体现了方程思想.
新知探究
在数轴上表示不等式的解集
如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
新知探究
练一练
4. 利用数轴来表示下列不等式的解集.
(1) x>-1 (2) x<
-1
0
0
1
用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
>、< 画空心圆.
新知探究
小归纳
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点表示;不包含在解集中,则用空心点表示.
(3)定方向:相对于边界点,大于向右画,小于向左画.
新知探究
小归纳
在数轴上表示不等式的解集时,一要把点找准确,二要找准方向,三要区别实心圆点与空心圆圈.
求不等式的特殊解,先要准确求出不等式的解集,然后确定特殊解.在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
03 典型例题
例题讲解
1. 不等式x>-2与x ≥-2的解集有什么不同?在数轴上表示它们时怎样区别?分别在数轴上把这两个解集表示出来.
例题讲解
2. 已知 是关于x的一元一次不等式,
则a的值是________.
解析:由 是关于x的一元一次不等式得2a-1=1,计算即可求出a的值等于1.
1
例题讲解
3. 下列说法:①x=0是2x-1<0的一个解;②x=-3不是3x-2>0的解;③-2x+1<0的解集是x>2.其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
解析:①x=0时,2x-1<0成立,所以x=0是2x-1<0的一个解;②x=-3时,3x-2>0不成立,所以x=-3不是3x-2>0的解;③-2x+1<0的解集是x> ,所以不正确.
C
例题讲解
4. 解不等式 12-6x≥2(1-2x),并把它的解集在数轴上表示出来.
解:去括号,得 12 -6x ≥ 2-4x
移项,得 -6x+4x ≥ 2-12
合并同类项,得 -2x ≥ -10
两边都除以-2,得 x ≤ 5
原不等式的解集在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
注意:x≤5中包含5,所以在数轴上将表示5的点画成实心圆点.
首先将括号去掉
将同类项放在一起
根据不等式基本性质2
例题讲解
5. 当x取什么值时,代数式 x +2的值大于或等于0?并求出所有满足条件的正整数.
解:根据题意,得 x +2≥ 0,
解得 x ≤ 6.
所以,当x≤6时,代数式 x+2的值大于或等于0.
x≤6在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
由图可知,满足条件的正整数有 1,2,3,4,5,6.
04 拓展提高
拓展提高
1.已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
解:由方程的定义,把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
其中正整数解有1和2.
-1
0
1
2
3
4
5
6
拓展提高
2. y为何值时,代数式 的值不大于代数式
的值,并求出满足条件的最大整数.
解:依题意,得
去分母得:4(5y+4)≤21-8(1-y),
去括号得:20y+16≤21-8+8y,
移项得:20y-8y≤21-8-16,
合并同类项得:12y≤-3,
把y的系数化为1得:y≤
在数轴上表示如下:
由图可知,满足条件的最大整数是-1.
05 课堂小结
课堂小结
一元一次不等式的解法
一元一次不等式的解集
解一元一次不等式
→
步骤
课堂小结
应用不等式的基本性质
↑
解一元一次不等式
→
将解集在数轴上表示
找符合条件的整数解
→
不等式解集的表示
↓
06 作业布置
完成课本习题 4.3 A、B组
作业布置
谢 谢 观 看
同课章节目录
