2018-2019学年黑龙江省哈尔滨十七中七年级(上)月考数学试卷(五四学制)(12月份)(解析版)
文档属性
| 名称 | 2018-2019学年黑龙江省哈尔滨十七中七年级(上)月考数学试卷(五四学制)(12月份)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 214.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-15 00:00:00 | ||
图片预览

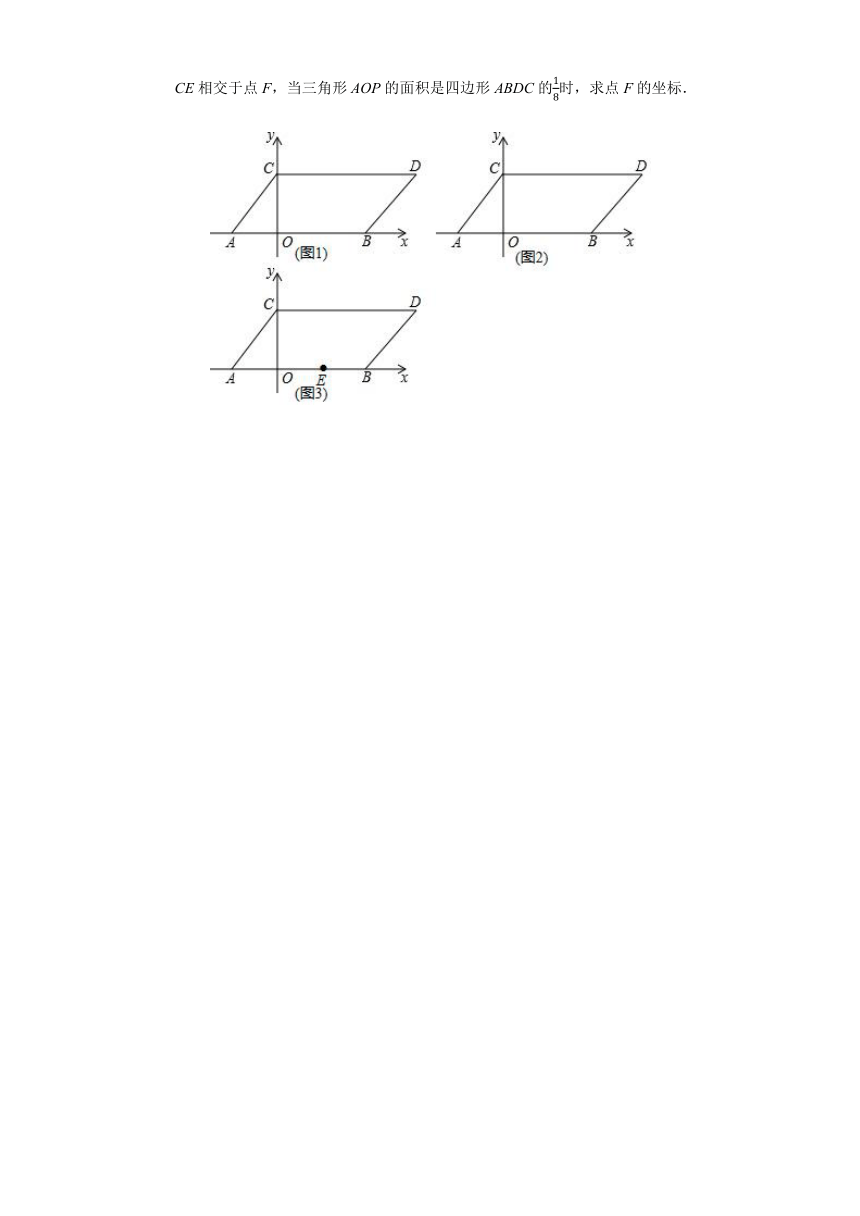
文档简介
2018-2019学年黑龙江省哈尔滨十七中七年级(上)月考数学试卷(五四学制)(12月份)
一、选择题(本大题共10小题,共30.0分)
下列各数中3.1415,-,0.131131113……,,-无理数的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
如图,将左图中的福娃“欢欢”通过平移可得到的图为( )
A. B. C. D.
运用等式性质进行的变形,正确的是( )
A. 如果,那么 B. 如果,那么
C. 如果,那么 D. 如果,那么
把方程去分母后,正确的是( )
A. B. C. D.
点M在第四象限,它到x轴、y轴的距离分别为8和5,则点M的坐标为( )
A. B. C. D.
如图,AB∥CD,AD∥BC,则下列各式中正确的是( )
A.
B.
C.
D. 与大小无法确定
一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是( )
A. 第一次右拐,第二次左拐
B. 第一次左拐,第二次右拐
C. 第一次左拐,第二次左拐
D. 第一次右拐,第二次右拐
如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于( )
A.
B.
C.
D.
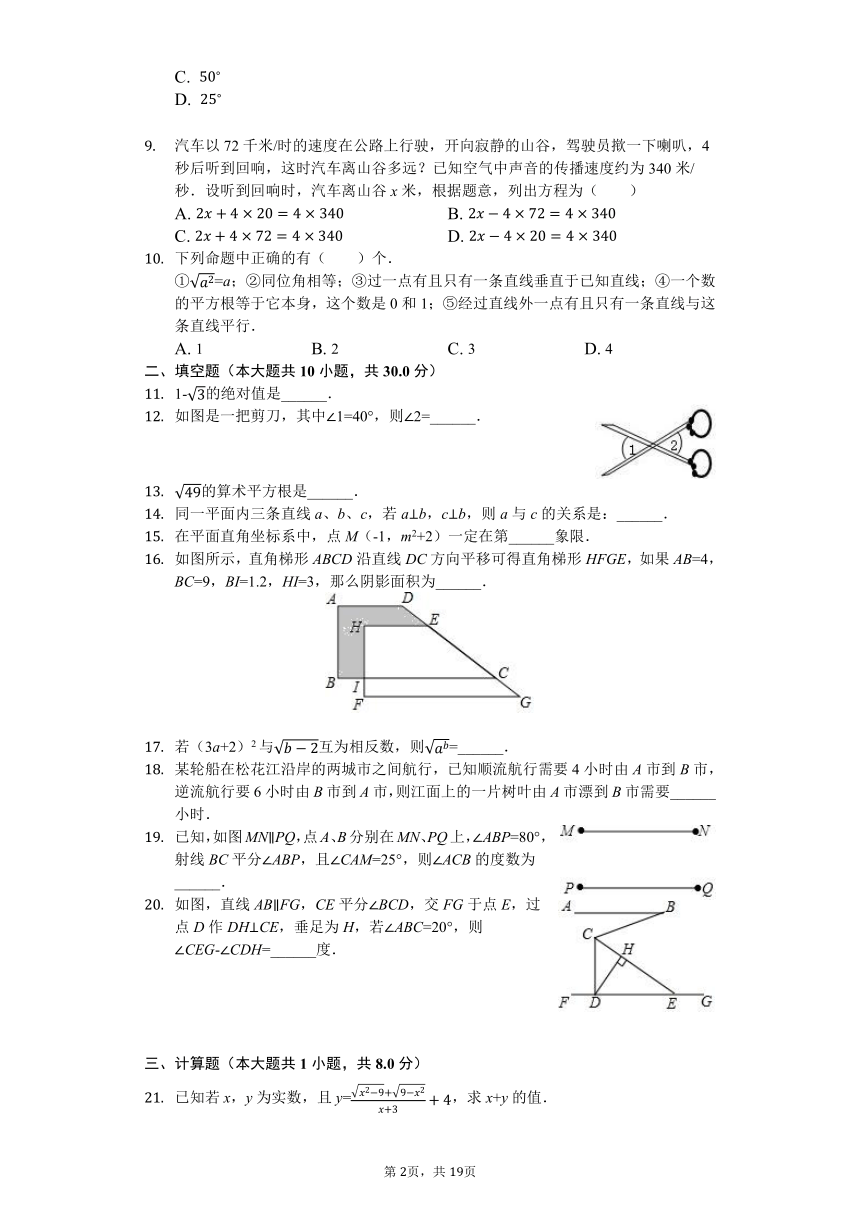
汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员揿一下喇叭,4秒后听到回响,这时汽车离山谷多远?已知空气中声音的传播速度约为340米/秒.设听到回响时,汽车离山谷x米,根据题意,列出方程为( )
A. B.
C. D.
下列命题中正确的有( )个.
①=a;②同位角相等;③过一点有且只有一条直线垂直于已知直线;④一个数的平方根等于它本身,这个数是0和1;⑤经过直线外一点有且只有一条直线与这条直线平行.
A. 1 B. 2 C. 3 D. 4
二、填空题(本大题共10小题,共30.0分)
1-的绝对值是______.
如图是一把剪刀,其中∠1=40°,则∠2=______.
的算术平方根是______.
同一平面内三条直线a、b、c,若a⊥b,c⊥b,则a与c的关系是:______.
在平面直角坐标系中,点M(-1,m2+2)一定在第______象限.
如图所示,直角梯形ABCD沿直线DC方向平移可得直角梯形HFGE,如果AB=4,BC=9,BI=1.2,HI=3,那么阴影面积为______.
若(3a+2)2与互为相反数,则=______.
某轮船在松花江沿岸的两城市之间航行,已知顺流航行需要4小时由A市到B市,逆流航行要6小时由B市到A市,则江面上的一片树叶由A市漂到B市需要______小时.
已知,如图MN∥PQ,点A、B分别在MN、PQ上,∠ABP=80°,射线BC平分∠ABP,且∠CAM=25°,则∠ACB的度数为______.
如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH=______度.
三、计算题(本大题共1小题,共8.0分)
已知若x,y为实数,且y=,求x+y的值.
四、解答题(本大题共6小题,共52.0分)
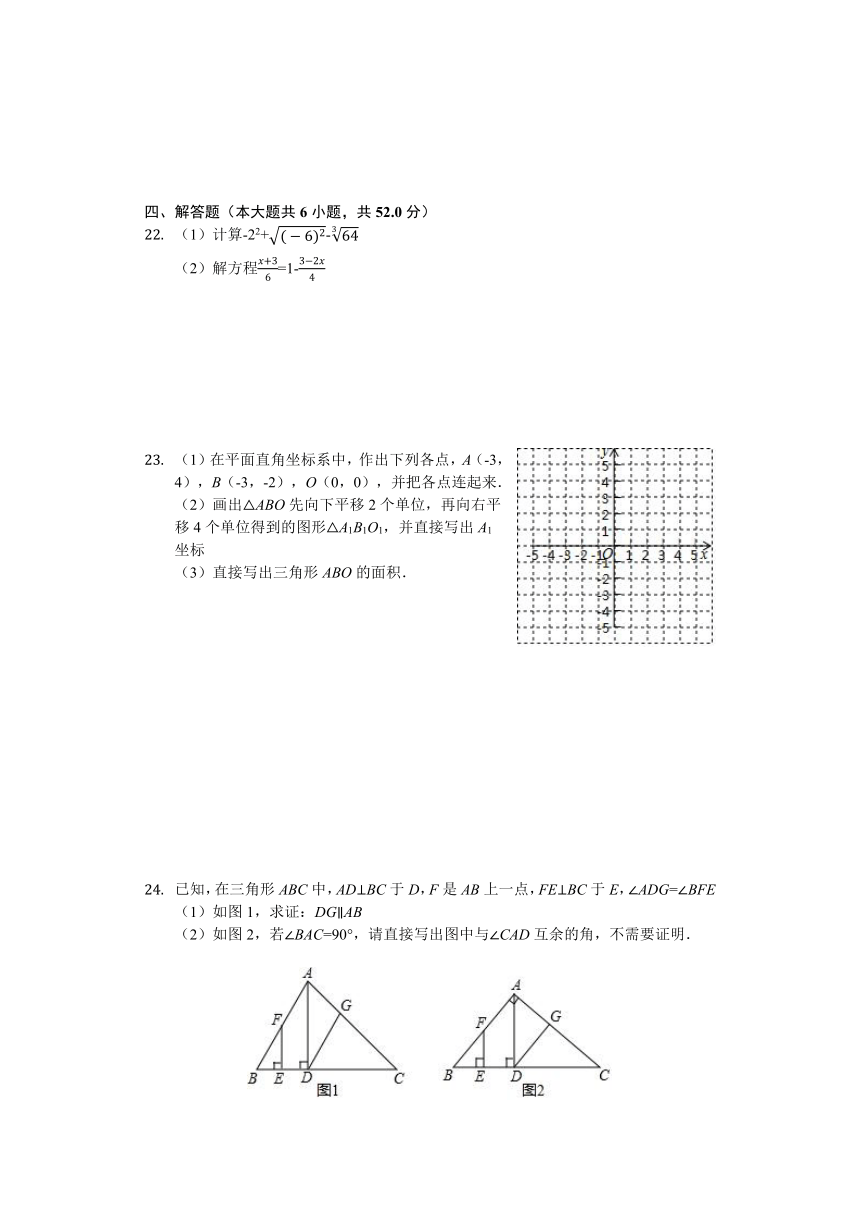
(1)计算-22+-
(2)解方程=1-
(1)在平面直角坐标系中,作出下列各点,A(-3,4),B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4个单位得到的图形△A1B1O1,并直接写出A1坐标
(3)直接写出三角形ABO的面积.
已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
(1)如图1,求证:DG∥AB
(2)如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.
冰封超市购进一批运动服,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每套运动服的售价为140元.
(1)求每套运动服的进价?
(2)超市卖出一半后,正好赶上双十一促销,商店决定将剩下的运动服每3套400元的价格出售,很快销售一空,这批运动服超市共获利14000元,求该超市共购进多少套运动服?
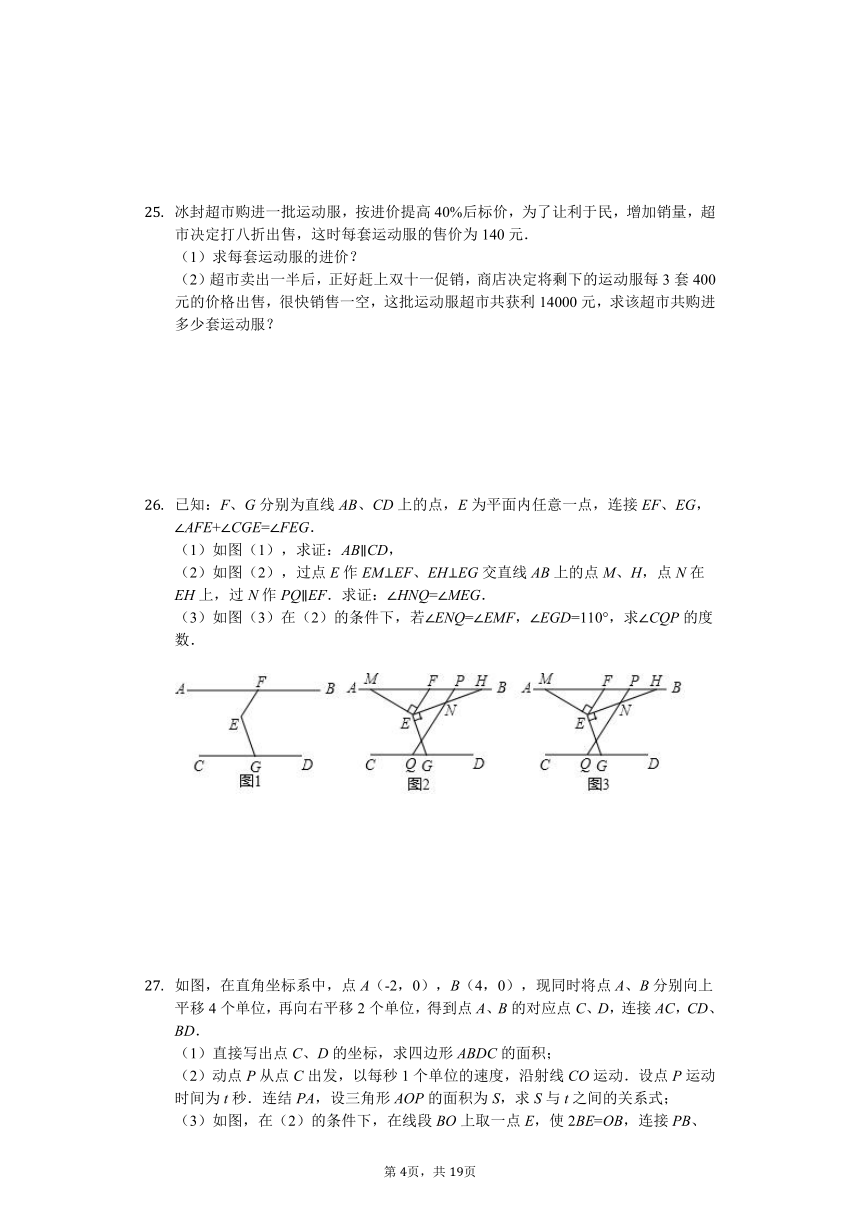
已知:F、G分别为直线AB、CD上的点,E为平面内任意一点,连接EF、EG,∠AFE+∠CGE=∠FEG.
(1)如图(1),求证:AB∥CD,
(2)如图(2),过点E作EM⊥EF、EH⊥EG交直线AB上的点M、H,点N在EH上,过N作PQ∥EF.求证:∠HNQ=∠MEG.
(3)如图(3)在(2)的条件下,若∠ENQ=∠EMF,∠EGD=110°,求∠CQP的度数.
如图,在直角坐标系中,点A(-2,0),B(4,0),现同时将点A、B分别向上平移4个单位,再向右平移2个单位,得到点A、B的对应点C、D,连接AC,CD、BD.
(1)直接写出点C、D的坐标,求四边形ABDC的面积;
(2)动点P从点C出发,以每秒1个单位的速度,沿射线CO运动.设点P运动时间为t秒.连结PA,设三角形AOP的面积为S,求S与t之间的关系式;
(3)如图,在(2)的条件下,在线段BO上取一点E,使2BE=OB,连接PB、CE相交于点F,当三角形AOP的面积是四边形ABDC的时,求点F的坐标.
答案和解析
1.【答案】B
【解析】
解:在3.1415,-,0.131131113……,,-中,无理数有-,0.131131113……,无理数的个数有2个.
故选:B.
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.【答案】C
【解析】
解:根据平移的定义可得左图中的福娃“欢欢”通过平移可得到的图为C,
故选:C.
根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移即可得到答案.
此题主要考查了平移,关键是掌握平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等.
3.【答案】C
【解析】
解:A、等式的左边加2,右边加3,故A错误;
B、等式的左边减2,右边减3,故B错误;
C、等式的两边都乘c,故C正确;
D、当a=0时,a≠3,故D错误;
故选:C.
根据等式的性质根据等式的基本性质:
①等式的两边同时加上或减去同一个数或字母,等式仍成立;
②等式的两边同时乘以或除以同一个不为0的数或字母,等式仍成立.即可解决.
本题主要考查了等式的基本性质,等式性质:
1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.
4.【答案】B
【解析】
解:-=1,
方程两边都乘以6得:3x-2(x-1)=6,
故选:B.
方程两边都乘以6即可得出答案.
本题考查了解一元一次方程的应用,注意:解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化成1.
5.【答案】B
【解析】
解:∵点M在第四象限,
∴点M的横坐标为正数,纵坐标为负数,
∵点M到x轴、y轴的距离分别为8和5,
∴点M的横坐标为5,纵坐标为-8,即M(5,-8).
故选:B.
根据第四象限点的坐标特点得到点M的横坐标为正数,纵坐标为负数,而点M到x轴的距离为8,则纵坐标为-8;点M到y轴的距离为5,则点M的横坐标为5,即M(5,-8).
本题考查了点的坐标:直角坐标系中点与有序实数对一一对应;在x轴上点的纵坐标为0,在y轴上点的横坐标为0;记住各象限点的坐标特点.
6.【答案】B
【解析】
解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴∠A=∠BCD,
∵∠3+∠BCD=180°,∠1+∠2+∠A=180°,
∴∠1+∠2=∠3.
故选:B.
根据题意,先判定四边形ABCD是平行四边形,再根据平行四边形的对角相等和三角形外角的性质进行判断即可.
本题考查平行四边形的性质和判定.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
7.【答案】C
【解析】
解:因为两次拐弯后,按原来的相反方向前进,
所以两次拐弯的方向相同,形成的角是同旁内角,且互补.
故选:C.
两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行,据此判断即可.
此题主要考查了平行线的性质,利用两直线平行,同旁内角互补得出是解题关键.
8.【答案】C
【解析】
解:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DEF=∠EFB=65°,
又由折叠的性质可得∠D′EF=∠DEF=65°,
∴∠AED′=180°-65°-65°=50°,
故选:C.
由平行可求得∠DEF,又由折叠的性质可得∠DEF=∠D′EF,结合平角可求得∠AED′.
本题主要考查平行线的性质及折叠的性质,掌握两直线平行内错角相等是解题的关键.
9.【答案】A
【解析】
解:设汽车离山谷x米,则汽车离山谷距离的2倍即2x,
因为汽车的速度是72千米/时即20米/秒,
则汽车前进的距离为:4×20米/秒,
声音传播的距离为:4×340米/秒,
根据等量关系列方程得:2x+4×20=4×340,
故选:A.
首先理解题意找出题中存在的等量关系:汽车离山谷距离的2倍+汽车前进的距离=声音传播的距离,根据等量关系列方程即可.
列方程解应用题的关键是找出题目中的相等关系.
10.【答案】A
【解析】
解:①=|a|,错误;
②两直线平行,同位角相等,错误;
③在同一平面内,过一点有且只有一条直线垂直于已知直线,错误;
④一个数的平方根等于它本身,这个数是0,错误;
⑤经过直线外一点有且只有一条直线与这条直线平行,正确;
故选:A.
根据二次根式、平行线的性质、平方根和平行线的判定判断即可.
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.
11.【答案】-1
【解析】
解:根据题意得:|1-|=-1,
故答案为:-1
原式利用绝对值的代数意义化简,计算即可得到结果.
此题考查了实数的性质,熟练掌握运算法则是解本题的关键.
12.【答案】40°
【解析】
解:∵∠1和∠2是对顶角,
∴∠2=∠1,(对顶角相等)
又∵∠1=40°,
∴∠2=40°(等量代换).
剪刀即对顶角的一个应用类型,根据对顶角相等解答.
本题考查对顶角的定义和性质,需要熟练记忆.
13.【答案】
【解析】
解:∵72=49,∴=7,
∵()2=7,
∴的算术平方根是,
故答案为:.
根据平方运算,可得算术平方根.
本题考查了算术平方根,平方运算是求平方根的关键,注意本题是求7的算术平方根.
14.【答案】a∥c
【解析】
解:∵a⊥b,c⊥b,
∴a∥c.
故答案是:a∥c.
根据平行线的性质:垂直于同一直线的两条直线互相平行可知直线a与直线c的关系是平行.
本题主要考查了平行线的性质:垂直于同一直线的两条直线互相平行.
15.【答案】二
【解析】
解:∵点(-1,m2+2)它的横坐标-1<0,纵坐标m2+2>0,
∴符合点在第二象限的条件,
故点(-1,m2+2)一定在第二象限.
故答案为:二.
根据点在第二象限的坐标特点解答即可.
本题主要考查平面直角坐标系中各象限内点的坐标的符号,关键是根据点在第二象限的坐标特点解答.
16.【答案】8.4
【解析】
解:∵直角梯形ABCD沿直线DC方向平移可得直角梯形HFGE,
∴HF=AB=4,FG=BC=9,直角梯形ABCD的面积=直角梯形HFGE的面积,
∵BI=1.2,HI=3,
∴IC=BC-BI=9-1.2=7.8,HI=HF-HI=4-3=1,
∴直角梯形IFGC的面积为:(7.8+9)×1÷2=8.4,
∵阴影面积=直角梯形ABCD的面积-直角梯形HICE的面积,
直角梯形IFGC的面积=直角梯形HFGE的面积-直角梯形HICE的面积,
∴阴影面积=直角梯形IFGC的面积=8.4,
故答案为:8.4.
阴影部分的面积为梯形ABCD的面积减去四边形HICE的面积,四边形IFGC的面积等于梯形HFGE的面积减去四边形HICE的面积,那么阴影部分的面积和四边形IFGC的面积相等,因此只需要算出四边形IFGC的面积,根据题目条件易知四边形IFGC的为直角梯形,根据公式求出即可.
本题考查了平移的性质,直角梯形,解题的关键是将阴影部分的面积转化到求直角梯形IFGC的面积.
17.【答案】
【解析】
解:由题意知(3a+2)2与互为相反数,
即:(3a+2)2+=0
∴3a+2=0,b-2=0
∴a=-,b=2
∴==
故答案为.
由(3a+2)2与互为相反数可知,(3a+2)2+=0,互为相反数两个非负数互为相反数,则各自为零,于是可求出a、b的值,进一步可得出的结果.
本题考查的是非负数的性质,两个非负数互为相反数,则各自为零.两个非负数通常可出现绝对值、偶次幂或者算术平方根等形式.
18.【答案】24
【解析】
解:设A、B两市间的距离为S,水流速度为V水,由题意可得
-=2V水
可得S=24V水
∴=24
即江面上的一片树叶由A市漂到B市需要的时间即为=24小时.
故答案为24.
设顺流速度、逆流速度、静水速度、水流速度分别为V顺、V逆、V静、V水,由于V顺=V静+V水,V逆=V静-V水可得V顺-V逆=2V水,于是设A、B两市间的距离为S,可得方程表达出S与V水的关系,而江面上的一片树叶由A市漂到B市需要的时间即为.
本题不直接设所需时间,而是利用顺流速度、逆流速度、静水速度、水流速度之间的关系得出V顺-V逆=2V水,从而进一步求出表达式的值得出时间.正确理清问题中的未知量之间的关系是解决本题的关键.
19.【答案】15°或65°
【解析】
解:如图,当点C在直线MN,直线PQ的中间时,设直线BC交MN于J.
∵BC平分∠ABP,∠ABP=80°,
∴∠PBC=∠ABC=40°,
∵MN∥PQ,
∴∠PBC=∠AJB=40°,
∴∠ACB=∠CJA+∠CAM=40°+25°=65°,
当点C′在直线MN的上方时,∠AC′B=∠AJC-∠C′AM=40°-25°=15°,
综上所述,满足条件的∠ACB的值为65°或15°,
故答案为65°或15°
分两种情形分别求解即可解决问题.
本题考查平行线的性质,三角形的外角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
20.【答案】110
【解析】
解:延长DC交AB于H.设∠CHB=α.
∵AB∥CD,
∴∠GDE=180°-∠DHB=180°-α,
∵∠BCD=∠BHC+∠ABC=α+20°,
∵CE平分∠BCD,
∴∠DCH=α+10°,
∵DH⊥BC,
∴∠CHD=90°,
∴∠CDH=90°-(α+10°)=80°-α,
∵∠CEG=∠CDE+∠DCE=180°-α+α+10°=190°-α,
∴∠CEG-∠CDH=190°-α-(80°-α)=110°,
故答案为110.
延长DC交AB于H.设∠CHB=α.用α表示出∠CEG,∠CDH即可解决问题.
本题考查平行线的性质,三角形的外角的性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
21.【答案】解:由题意,x2-9≥0,9-x2≥0
∴x2=9,
∴x=±3
又∵x+3≠0,
∴x≠-3,
∴x=3,y=0+0+4=4,
∴x+y=7
【解析】
先根据二次根式有意义的条件得出x的值,代回代数式求出y的值,继而代入计算可得.
本题主要考查二次根式的性质与化简,解题的关键是掌握二次根式和分式有意义的条件.
22.【答案】解:(1)原式=-4+6-4
=6;
(2)=1-
去分母得:2(x+3)=12-3(3-2x)
?2x+6=12-9+6x
2x-6x=3-6
移项合并同类项的:-4x=-3
解得:x=.
【解析】
(1)直接利用立方根以及算术平方根的性质化简进而得出答案;
(2)直接去分母进而解方程得出答案.
此题主要考查了实数运算以及解一元一次方程,正确记忆相关数据是解题关键.
23.【答案】解:(1)如图所示,△ABO即为所求;
(2)如图所示,△A1B1O1即为所求,A1坐标为(1,2);
(3)△ABO的面积为×6×3=9.
【解析】
(1)根据三个点的坐标描点,再首尾顺次连接即可得;
(2)将三个顶点分别向下平移2个单位,再向右平移4个单位得到对应点,首尾顺次连接即可得;
(3)根据三角形的面积公式计算可得.
本题考查了利用平移变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
24.【答案】(1)证明:∵AD⊥BC,FE⊥BC,
∴∠DAB=∠FEB=90°,
∴AD∥EF,
∴∠BFE=∠BAD,
∵∠ADG=∠BFE,
∴∠BAD=∠ADG,
∴DG∥AB.
(2)与∠CAD互余的角有:∠BAD,∠BFE,∠ADG,∠C.
【解析】
(1)想办法证明∠BAD=∠ADG即可解决问题.
(2)利用直角三角形两锐角互余条件平行线的性质即可解决问题.
本题考查平行线的性质,直角三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
25.【答案】解:(1)设每套运动服的进价为x元
(1+40%)×80%x=140
∴x=125
答:每套运动服的进价为125元.
(2)设该超市共购进m套运动服
(140-125)×+(-125)×=14000
∴m=1200
答:该超市共购进1200套运动服.
【解析】
(1)设每套运动服的进价为x元.进价×(1+40%)×八折=售价;
(2)设该超市共购进m套运动服,根据“将剩下的运动服每3套400元的价格出售,很快销售一空,这批运动服超市共获利14000元”列出方程并解答.
本题考查了一元一次方程的应用.关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.
26.【答案】解:
(1)过E作ET∥AB
则,∠AFE=∠FET
∵∠FET+∠TEG=∠FEG,
∴∠AFE+∠TEG=∠FEG,
∵∠AFE+∠CGE=∠FEG
∴∠TEG=∠CGE
∴ET∥CD
∴AB∥CD,
(2)如图2
∵EM⊥EF、EH⊥EG
∴∠MEF=∠HEG=90°
∴∠MEG+∠FEH=180°
∵PQ∥EF
∴∠PNH=∠FEH
∵∠PNE+∠PNH=180°,∠HNQ=∠PNE
∴∠HNQ=∠MEG
(3)如图3
过点E作ER∥AB,由(1)知AB∥ER∥CD
∴∠AME+∠REG=180°,∠REG+∠EGC=180°,
∴∠AME+∠REG+∠REG+∠EGC=360°,
即∠AME+∠AEG+∠EGC=360°,
∵∠ENQ=∠EMF,
∴∠AME=∠HNQ,
由(2)知∠HNQ=∠MEG
∴∠AME=∠MEG
∵∠EGD=110°
∴∠EGC=180°-∠EGD=70°
∴∠AME=∠MEG=═145°
∴∠EMF=180°-∠AME=35°,
在Rt△MEF中,∠MFE=90°-∠EMF=55°
∵EF∥PQ,
∴∠MPQ=∠MFE=55°,
∴∠CQP=180°-∠MPQ=180°-55°=125°
故∠CQP的度数为125°
【解析】
(1)过E作ET∥AB,得到∠AFE=∠FET,再由已知条件,得到∠TEG=∠EGC,由平行线的判定即可证明;
(2)根据PQ∥EF得∠PNH=∠FEH,再由∠MEG+∠FEH=180°,∠PNH+∠HNQ=180°得到等角的补角相等即可解决问题;
(3)如图3中,过E作ER∥AB,可证得AE∥ER∥CD得到∠AME+∠MEG+∠EGC=360°,由PQ∥EF,得∠CQP+∠MPQ=180°,此问只要求出∠MPQ即可求解;
本题考查平行线的性质、垂线的性质、三角形的内角和定理等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.
27.【答案】解:(1)∵点A(-2,0),B(4,0),同时将点A、B分别向上平移4个单位,再向右平移2个单位,
得到点A、B的对应点C、D,
∴四边形ABDC是平行四边形,C(-2+2,0+4),D(4+2,0+4),AB=OA+OB=6,OC=4,
即C(0,4),D(6,4);
∴四边形ABDC的面积=AB×OC=6×4=24;
(2)分两种情况:
①点P在点O上方时,如图1所示:
由题意得:PC=t,OA=2,
∴OP=4-t,
∴△AOP的面积S=OA×OP=×2×(4-t)=4-t,
即S=4-t;
②点P在点O下方时,如图2所示:
由题意得:PC=t,OA=2,
∴OP=t-4,
∴△AOP的面积S=OA×OP=×2×(t-4)=t-4,
即S=t-4;
综上所述,△AOP的面积S与t之间的关系式为S=4-t,或S=t-4;
(3)分两种情况:
①点P在点O上方时,如图3所示:
∵△AOP的面积是四边形ABDC的,
∴4-t=×24=3,
解得:t=3,
∴OP=3,P(0,3),
∵2BE=OB=4,
∴OE=2,E(0,2),
设CE的解析式为y=kx+b,
由题意得:,解得:,
∴CE的解析式为y=-2x+4,
同理:BP的解析式为y=-x+3,
联立方程组得:,
解得:,即F(,);
②点P在点O下方时,如图4所示:
∵△AOP的面积是四边形ABDC的,
∴t-4=×24=3,
解得:t=7,PC=7,
∴OP=PC-OC=3,P(0,-3),
同①得,CE的解析式y=-2x+4,BP的解析式为y=x-3,
联立方程组得:,
解得:,即F(,-);
综上所述,当△AOP的面积是四边形ABDC的时,点F的坐标为(,)或(,-).
【解析】
(1)由平移的性质即可得出四边形ABDC是平行四边形和点C、D的坐标;
(2)分两种情况:①点P在点O上方时,由题意得:PC=t,OA=2,得出OP=4-t,由三角形面积公式即可得出结果;
②点P在点O下方时,由题意得:PC=t,OA=2,得出OP=t-4,由三角形面积公式即可得出结果;
(3)分两种情况::①点P在点O上方时,由题意得出4-t=×24=3,解得:t=3,得出OP=3,P(0,3),E(0,2),由待定系数法求出设CE和BP的解析式,再联立方程组求出即可;
②点P在点O下方时,解法同①.
本题是四边形综合题目,考查了平行四边形的判定与性质、平移的性质、坐标与图形性质、三角形面积公式、待定系数法求直线的解析式以及方程组的解法等知识;本题综合性强,熟练掌握平行四边形的性质和待定系数法求直线的解析式是解题的关键.
第2页,共2页
同课章节目录
