七年级数学上册第5章相交线与平行线5.1相交线同步课件(3课时52张ppt)(新版)华东师大版
文档属性
| 名称 | 七年级数学上册第5章相交线与平行线5.1相交线同步课件(3课时52张ppt)(新版)华东师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-16 17:37:30 | ||
图片预览










文档简介
课件52张PPT。教学课件
数学 七年级上册 华东师大版
第5章 相交线与平行线
5.1 相交线
5.1 相交线
5.1.1 对顶角1.掌握对顶角的定义并能够在图形中识别出来.
2.能够用对顶角的性质解决有关的问题.大桥上的钢梁和钢索棋盘上的横线和竖线 学校操场上的双杠,教室中课桌面、黑板面相邻的两条边与相对的两条边……都给我们以平行线、相交线的形象.请你画出任意两条相交直线,看看这四个角有什
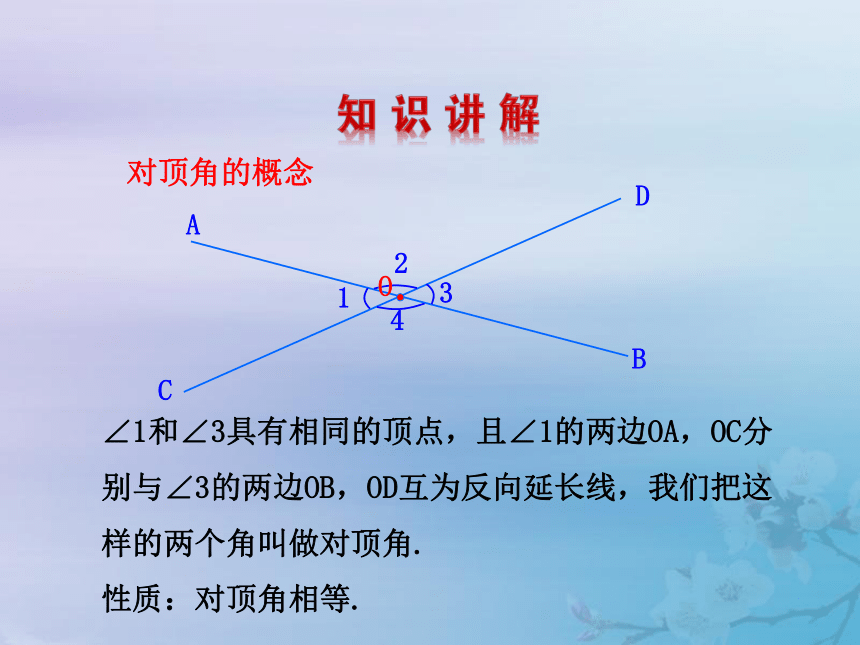
么关系?问题:两条相交直线形成的小于平角的角有几个?观察用剪刀剪布片的过程中有关角的变化. 任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系?它们的大小关系如何?∠3∠1∠2∠4∠1和∠2,4∠2和∠∠ 和∠,∠ 和∠143 4∠1和∠3,∠ 和∠ 2 3,对顶角的概念2314ABD∠1和∠3具有相同的顶点,且∠1的两边OA,OC分别与∠3的两边OB,OD互为反向延长线,我们把这样的两个角叫做对顶角.
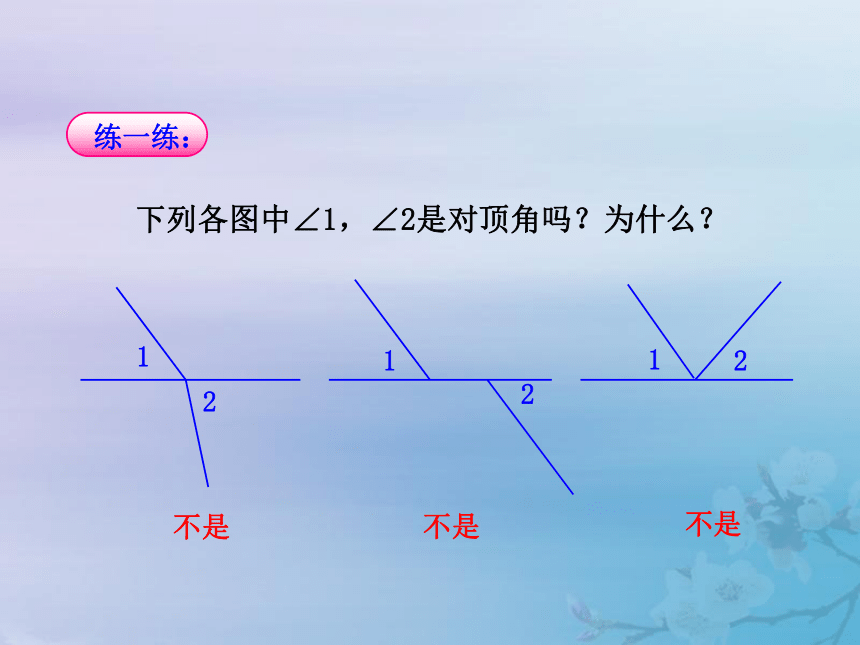
性质:对顶角相等.CO1下列各图中∠1,∠2是对顶角吗?为什么?21221不是不是不是【例】已知:直线a,b相交,∠1=40°.
求∠2,∠3,∠4的度数. 解:∠3=∠1=40° (对顶角相等),
∠2=180°-∠1=180°-40°=140°(平角的定义),
∠4=∠2=140°(对顶角相等). 1. 如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A.20° B.25° C.30° D.70°【解析】选D.因为∠1=40°,所以∠BOC=140°,因为OD平分∠BOC,所以∠2=70°.2.如图,三条直线AB,CD,EF相交于一点O,∠AOC的对顶角是 ,∠COF的对顶角是_______. ∠BOD∠EOD3.如图,∠1=∠2,则∠2与∠3的关系是 ,∠1与∠3的关系是 .123互补互补4. 一个角的补角是36°35′,这个角的度数 . 【解析】根据互为补角的定义,这个角=180°-36°35′=143°25′.
答案:143°25′通过本课时的学习,需要我们掌握对顶角的相关知识如下:
1.特征: ①两条直线相交形成的角;
②有一个公共顶点;
③没有公共边.
2.性质: 对顶角相等5.1.2 垂线1.在丰富的现实情境中,通过画、折等活动,进一步丰富对两条直线互相垂直的认识,掌握有关的符号表示.
2.会借助三角尺、量角器、方格纸画垂线,进一步丰富操作活动的经验.
3.在操作活动中,探索有关垂直的一些性质.平面内的两条直线有哪些位置关系?平行相交下面两种相交的情况有什么不同?两直线不垂直两直线垂直4.怎样用符号表示两条直线的垂直关系?1.什么叫做两条直线互相垂直?2.你能用三角尺、直尺、量角器画互相垂直的直线吗?5.过一点能画多少条已知直线的垂线?6.你是如何理解点到直线的距离的?3.怎样用折纸法折出垂线?定义:当两条直线AB,CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直.OBACD(1)你能用三角尺在白纸上画两条互相垂直的直线吗? (3)如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?(2)你能用量角器在白纸上画两条互相垂直的直线吗? 用三角尺作两条互相垂直的直线根据图示能折出互相垂直的直线,您不妨试试看!O图中,直线AB与直线CD垂直,记作:AB⊥CD;直线 m 与直线 n 垂直,记作:m⊥n ;互相垂直的两条直线的交点叫做垂足.是图形中“垂直(直角)” 的标记.垂直的表示在图中过点A作m的垂线,你能作多少条? ·A ·Amm平面内,过一点有且只有一条直线与已知直线垂直.看图回答你能用一句话表示这个结论吗?从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.直线外一点与直线上各点连成的所有线段中,垂线段最短.线段PA,PB,PC,PD谁最短?线段PB叫做点A到直线m的垂线段.【例】作一条直线l,在直线l上取一点A,在l外取一点B,试分别过点A,B用三角尺作直线的垂线.找出下图中互相垂直的直线.(1)(2)ABCDOBO⊥OD(或AO⊥OC)AC⊥BC(或CD⊥AB)【跟踪训练】1. 如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是( )
A.125° B.135°
C.145° D.155°【解析】选B.因为OE⊥AB,所以∠BOE=90°,又因为∠BOD=45°,所以∠EOD=45°,因为∠COD=180°,所以∠COE=∠COD- ∠ EOD=180°-45°=135°.2. 如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°【解析】选B.因为OC⊥OD,所以∠COD=90°,又因为∠AOB=180°,
所以∠DOB=∠AOB-∠COD-∠COA=180°-90°-36°=54°.3.如图,直线AB⊥CD,垂足为O,射线OP在∠AOD的内部,且∠POA=4∠POD,则∠COP︰∠BOP的值为( )
A.3︰2 B. 4︰1
C.9︰1 D. 5︰3 【解析】选A.因为AB⊥CD,所以∠AOD=90°,又因为∠POA=4∠POD,所以∠POA+∠POD=4∠POD+∠POD = ∠AOD= 90°,所以∠POD =18°,∠POA=4×18°=72°,
所以∠COP=∠COA+∠POA=90°+72°=162°,
∠BOP=∠BOD+∠POD=90°+18°=108°.
所以∠COP︰∠BOP=162°︰108°= 3︰2. 1.垂直的定义.
2.垂直的画法.
3.垂直的记法.
4.垂直的一个结论.
5.点到直线的距离.
6.丰富了对平行、垂直和角的认识. 对人不尊敬,首先就是对自己的不尊敬.5.1.3 同位角、内错角、同旁内角1.认识两条直线被第三条直线所截而产生的三种角——同位角、内错角、同旁内角.
2.能从复杂图形中找出基本图形,增强对图形的认识. 如图,两条直线a,b相交形成四个角∠1,∠2,
∠3,∠4∠1与∠3 ∠2与∠4 对顶角:互补的角:∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 1.两条直线被第三条直线所截(1)直线l与两直线a,b分别相交于点P,Q
(2)直线l截直线a,b于点P,Q
(3)直线a,b被直线l所截直线l叫做截线直线a,b叫做被截直线你认为截线和被截直线该怎样区分?问题:你能说出以下这些图形,哪两条直线被第三条
直线所截吗?直线a,b被直线l所截直线BC,DE 被直线AB所截labB在一个平面内,一条直线l与两条直线a,b分别相交于点P,Q(直线l 分别截直线a,b于点P,Q 或者就说两条直线a,b被直线l所截).两条直线被第三条直线所截,形成“三线八角”的图形.截线PQ图中∠1与∠5的位置有什么关系呢?∠1与∠5处于直线l
的_______,上方上方 且分别在直线a,b的
_______.这样位置的一对角就是 _______.像这样位于截线l的同侧,在两条被截直线a,b的同一方的同位角还有________、_________、__________. ∠2与∠6∠3与∠7∠4与∠8(1)同位角同一侧同一方同位角左 右2.特殊位置的角图中∠3与∠5的位置有什么关系呢?∠3与∠5处于直线l的_____,直线a,b的_________,这样位置的一对角就是
_______.像这样位于截线l的两侧,在两条直线a,b的内部的内错角还有 . ∠4与∠6左 右(2)内错角内 部两侧内部交错内错角图中∠4与∠5的位置有什么关系呢?∠4与∠5处于直线l的
_______,
_____,这样位置的一对角就是_________.像这样位于截线l的同侧,两条直线a,b的内部的同旁内角还有 . ∠3与∠6(3)同旁内角左 右同一侧同旁内角内部直线a,b的在两被截直线的内部,在截线的两侧内部交错 在两被截直线的内部,截线的同侧同位角 内错角同旁
内角位置关系基本模型在两被截直线的同一方,
在截线的同一侧位置相
同同位角、内错角、同旁内角是三种特殊位置关系的角,在找这些角时,要注意到两个角的公共边所在的直线是截线,其余两边是两条被截直线.1.如图,所标的六个角中,
∠1与 是同位角;
∠5与 是同旁内角;
∠2与 是内错角.∠6∠3 或∠4∠1 2.根据图形按要求填空:
(1)∠1与∠2是直线 和 被直线
所截而得的 .BCABDE同位角 做事是否成功,不在一时奋发,而在能否坚持.
数学 七年级上册 华东师大版
第5章 相交线与平行线
5.1 相交线
5.1 相交线
5.1.1 对顶角1.掌握对顶角的定义并能够在图形中识别出来.
2.能够用对顶角的性质解决有关的问题.大桥上的钢梁和钢索棋盘上的横线和竖线 学校操场上的双杠,教室中课桌面、黑板面相邻的两条边与相对的两条边……都给我们以平行线、相交线的形象.请你画出任意两条相交直线,看看这四个角有什
么关系?问题:两条相交直线形成的小于平角的角有几个?观察用剪刀剪布片的过程中有关角的变化. 任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系?它们的大小关系如何?∠3∠1∠2∠4∠1和∠2,4∠2和∠∠ 和∠,∠ 和∠143 4∠1和∠3,∠ 和∠ 2 3,对顶角的概念2314ABD∠1和∠3具有相同的顶点,且∠1的两边OA,OC分别与∠3的两边OB,OD互为反向延长线,我们把这样的两个角叫做对顶角.
性质:对顶角相等.CO1下列各图中∠1,∠2是对顶角吗?为什么?21221不是不是不是【例】已知:直线a,b相交,∠1=40°.
求∠2,∠3,∠4的度数. 解:∠3=∠1=40° (对顶角相等),
∠2=180°-∠1=180°-40°=140°(平角的定义),
∠4=∠2=140°(对顶角相等). 1. 如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A.20° B.25° C.30° D.70°【解析】选D.因为∠1=40°,所以∠BOC=140°,因为OD平分∠BOC,所以∠2=70°.2.如图,三条直线AB,CD,EF相交于一点O,∠AOC的对顶角是 ,∠COF的对顶角是_______. ∠BOD∠EOD3.如图,∠1=∠2,则∠2与∠3的关系是 ,∠1与∠3的关系是 .123互补互补4. 一个角的补角是36°35′,这个角的度数 . 【解析】根据互为补角的定义,这个角=180°-36°35′=143°25′.
答案:143°25′通过本课时的学习,需要我们掌握对顶角的相关知识如下:
1.特征: ①两条直线相交形成的角;
②有一个公共顶点;
③没有公共边.
2.性质: 对顶角相等5.1.2 垂线1.在丰富的现实情境中,通过画、折等活动,进一步丰富对两条直线互相垂直的认识,掌握有关的符号表示.
2.会借助三角尺、量角器、方格纸画垂线,进一步丰富操作活动的经验.
3.在操作活动中,探索有关垂直的一些性质.平面内的两条直线有哪些位置关系?平行相交下面两种相交的情况有什么不同?两直线不垂直两直线垂直4.怎样用符号表示两条直线的垂直关系?1.什么叫做两条直线互相垂直?2.你能用三角尺、直尺、量角器画互相垂直的直线吗?5.过一点能画多少条已知直线的垂线?6.你是如何理解点到直线的距离的?3.怎样用折纸法折出垂线?定义:当两条直线AB,CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直.OBACD(1)你能用三角尺在白纸上画两条互相垂直的直线吗? (3)如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?(2)你能用量角器在白纸上画两条互相垂直的直线吗? 用三角尺作两条互相垂直的直线根据图示能折出互相垂直的直线,您不妨试试看!O图中,直线AB与直线CD垂直,记作:AB⊥CD;直线 m 与直线 n 垂直,记作:m⊥n ;互相垂直的两条直线的交点叫做垂足.是图形中“垂直(直角)” 的标记.垂直的表示在图中过点A作m的垂线,你能作多少条? ·A ·Amm平面内,过一点有且只有一条直线与已知直线垂直.看图回答你能用一句话表示这个结论吗?从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.直线外一点与直线上各点连成的所有线段中,垂线段最短.线段PA,PB,PC,PD谁最短?线段PB叫做点A到直线m的垂线段.【例】作一条直线l,在直线l上取一点A,在l外取一点B,试分别过点A,B用三角尺作直线的垂线.找出下图中互相垂直的直线.(1)(2)ABCDOBO⊥OD(或AO⊥OC)AC⊥BC(或CD⊥AB)【跟踪训练】1. 如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是( )
A.125° B.135°
C.145° D.155°【解析】选B.因为OE⊥AB,所以∠BOE=90°,又因为∠BOD=45°,所以∠EOD=45°,因为∠COD=180°,所以∠COE=∠COD- ∠ EOD=180°-45°=135°.2. 如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°【解析】选B.因为OC⊥OD,所以∠COD=90°,又因为∠AOB=180°,
所以∠DOB=∠AOB-∠COD-∠COA=180°-90°-36°=54°.3.如图,直线AB⊥CD,垂足为O,射线OP在∠AOD的内部,且∠POA=4∠POD,则∠COP︰∠BOP的值为( )
A.3︰2 B. 4︰1
C.9︰1 D. 5︰3 【解析】选A.因为AB⊥CD,所以∠AOD=90°,又因为∠POA=4∠POD,所以∠POA+∠POD=4∠POD+∠POD = ∠AOD= 90°,所以∠POD =18°,∠POA=4×18°=72°,
所以∠COP=∠COA+∠POA=90°+72°=162°,
∠BOP=∠BOD+∠POD=90°+18°=108°.
所以∠COP︰∠BOP=162°︰108°= 3︰2. 1.垂直的定义.
2.垂直的画法.
3.垂直的记法.
4.垂直的一个结论.
5.点到直线的距离.
6.丰富了对平行、垂直和角的认识. 对人不尊敬,首先就是对自己的不尊敬.5.1.3 同位角、内错角、同旁内角1.认识两条直线被第三条直线所截而产生的三种角——同位角、内错角、同旁内角.
2.能从复杂图形中找出基本图形,增强对图形的认识. 如图,两条直线a,b相交形成四个角∠1,∠2,
∠3,∠4∠1与∠3 ∠2与∠4 对顶角:互补的角:∠1与∠2 ∠2与∠3 ∠3与∠4 ∠4与∠1 1.两条直线被第三条直线所截(1)直线l与两直线a,b分别相交于点P,Q
(2)直线l截直线a,b于点P,Q
(3)直线a,b被直线l所截直线l叫做截线直线a,b叫做被截直线你认为截线和被截直线该怎样区分?问题:你能说出以下这些图形,哪两条直线被第三条
直线所截吗?直线a,b被直线l所截直线BC,DE 被直线AB所截labB在一个平面内,一条直线l与两条直线a,b分别相交于点P,Q(直线l 分别截直线a,b于点P,Q 或者就说两条直线a,b被直线l所截).两条直线被第三条直线所截,形成“三线八角”的图形.截线PQ图中∠1与∠5的位置有什么关系呢?∠1与∠5处于直线l
的_______,上方上方 且分别在直线a,b的
_______.这样位置的一对角就是 _______.像这样位于截线l的同侧,在两条被截直线a,b的同一方的同位角还有________、_________、__________. ∠2与∠6∠3与∠7∠4与∠8(1)同位角同一侧同一方同位角左 右2.特殊位置的角图中∠3与∠5的位置有什么关系呢?∠3与∠5处于直线l的_____,直线a,b的_________,这样位置的一对角就是
_______.像这样位于截线l的两侧,在两条直线a,b的内部的内错角还有 . ∠4与∠6左 右(2)内错角内 部两侧内部交错内错角图中∠4与∠5的位置有什么关系呢?∠4与∠5处于直线l的
_______,
_____,这样位置的一对角就是_________.像这样位于截线l的同侧,两条直线a,b的内部的同旁内角还有 . ∠3与∠6(3)同旁内角左 右同一侧同旁内角内部直线a,b的在两被截直线的内部,在截线的两侧内部交错 在两被截直线的内部,截线的同侧同位角 内错角同旁
内角位置关系基本模型在两被截直线的同一方,
在截线的同一侧位置相
同同位角、内错角、同旁内角是三种特殊位置关系的角,在找这些角时,要注意到两个角的公共边所在的直线是截线,其余两边是两条被截直线.1.如图,所标的六个角中,
∠1与 是同位角;
∠5与 是同旁内角;
∠2与 是内错角.∠6∠3 或∠4∠1 2.根据图形按要求填空:
(1)∠1与∠2是直线 和 被直线
所截而得的 .BCABDE同位角 做事是否成功,不在一时奋发,而在能否坚持.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
