七年级数学上册第2章有理数2.4绝对值与相反数教学课件(17张ppt)(新版)苏科版
文档属性
| 名称 | 七年级数学上册第2章有理数2.4绝对值与相反数教学课件(17张ppt)(新版)苏科版 |

|
|
| 格式 | zip | ||
| 文件大小 | 385.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-17 00:00:00 | ||
图片预览





文档简介
课件17张PPT。教学课件
数学 七年级上册 江苏科技版
第2章 有理数
2.4 绝对值与相反数 小明的家在学校西边3 km处,小丽的家在学校东边2 km处.假如他们步行的速度相同,谁先到学校?
思考:1.A,B两点离原点的距离各是多少?
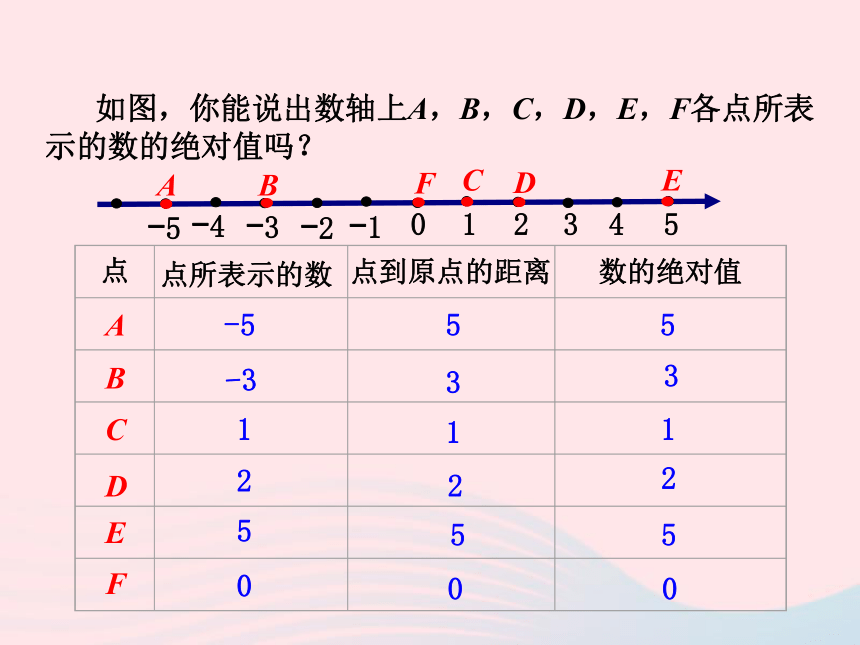
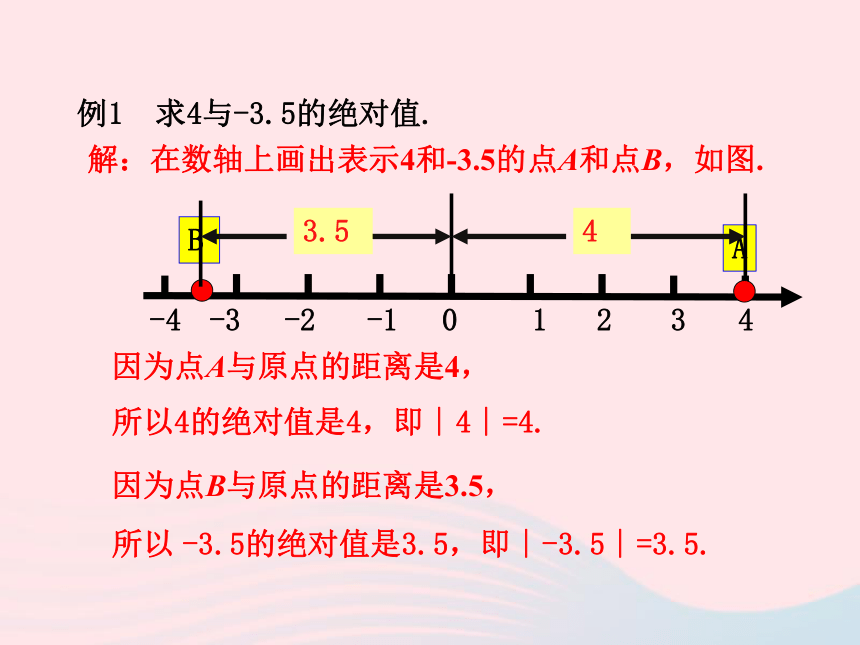
2.A,B两点离原点的距离与它们表示的数是正数还是负数有没有关系? 一、绝对值的概念和性质 如图,你能说出数轴上A,B,C,D,E,F各点所表示的数的绝对值吗?ABCDEF-555-333111222555000有理数的绝对值的求法:1.画数轴,标出有理数所在的点,得到点到原点的距离.2.求得有理数的绝对值.例1 求4与-3.5的绝对值.解:在数轴上画出表示4和-3.5的点A和点B,如图.因为点A与原点的距离是4,所以4的绝对值是4,即∣4∣=4.因为点B与原点的距离是3.5,所以 -3.5的绝对值是3.5,即∣-3.5∣=3.5.2.(1)到原点距离为3的数是 .(2)绝对值为3的数是 .(3)绝对值为-3的数是 .5.“任何数的绝对值都是正数”的说法对吗?练一练3.绝对值最小的数是 .4.绝对值小于4.5是 . 1.观察数轴上点A,B的位置及其到原点的距离,你有什么发现?解:(1)点A,B在原点两侧,分别表示-5和5;(2)点A,B与原点的距离都是5.二、相反数的概念及其表示相反数的几何意义:
几何意义:位于原点两侧且到原点距离相等的点所表示的两个数.2.观察下列各对有理数,从符号和绝对值方面你发现了什么?
5与-5; 2.5与-2.5;与与相反数的代数意义:
代数意义:符号不同、绝对值相同的两个数称作互为相反数,其中一个是另一个的相反数.解:符号不同、绝对值相同.
3.如何表示4,-3.5, 的相反数?
解:4的相反数为-4;-3.5的相反数为3.5;
的相反数为
相反数的表示:
(1)表示一个数(不是0)的相反数,可以再这个数的前面添一个“-”,即数a的相反数为-a.
(2)0的相反数是0.例2 求下列各数的相反数:
58,-4,3.14.解:58的相反数为-58;
-4的相反数为4;
3.14的相反数为-3.14.例3 填空:(1)3.5的相反数表示为 ;(2)-2.5的相反数表示为 ;(3)-(+4)是 的相反数;(4)-(-7)是 的相反数.-(-2.5)4-3.5-7思考:如何化简化简多重符号的方法:根据相反数的求法逐步由内向外化简.例4 化简:(1)-(+2.5)= ;(2)-(-2.5)= ;(3)+(-2.5)= ;(4)+(+2.5)= .-2.5-2.5+2.5+2.5三、绝对值的性质(1)绝对值是它本身的数是非负数,绝对值是它的相反数的数是非正数,0是绝对值最小的数.
(2)任何数都有且只有一个绝对值,任何数的绝对值都是非负数.
(3)绝对值是某个正数的数有两个,它们互为相反数.
(4)互为相反数的两个数的绝对值相等,反之,绝对值相等的两个数可能相等,也可能互为相反数.例2 比较-3与-6的大小.解:因为∣-3∣=3,∣-6∣=6,且3 < 6,
所以-3 > -6.四、利用绝对值比较数的大小法则:
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.比较-3,-0.4,-2的绝对值的大小,并用“<”把它们连接起来.练一练谈谈你这一节课有哪些收获.小结
数学 七年级上册 江苏科技版
第2章 有理数
2.4 绝对值与相反数 小明的家在学校西边3 km处,小丽的家在学校东边2 km处.假如他们步行的速度相同,谁先到学校?
思考:1.A,B两点离原点的距离各是多少?
2.A,B两点离原点的距离与它们表示的数是正数还是负数有没有关系? 一、绝对值的概念和性质 如图,你能说出数轴上A,B,C,D,E,F各点所表示的数的绝对值吗?ABCDEF-555-333111222555000有理数的绝对值的求法:1.画数轴,标出有理数所在的点,得到点到原点的距离.2.求得有理数的绝对值.例1 求4与-3.5的绝对值.解:在数轴上画出表示4和-3.5的点A和点B,如图.因为点A与原点的距离是4,所以4的绝对值是4,即∣4∣=4.因为点B与原点的距离是3.5,所以 -3.5的绝对值是3.5,即∣-3.5∣=3.5.2.(1)到原点距离为3的数是 .(2)绝对值为3的数是 .(3)绝对值为-3的数是 .5.“任何数的绝对值都是正数”的说法对吗?练一练3.绝对值最小的数是 .4.绝对值小于4.5是 . 1.观察数轴上点A,B的位置及其到原点的距离,你有什么发现?解:(1)点A,B在原点两侧,分别表示-5和5;(2)点A,B与原点的距离都是5.二、相反数的概念及其表示相反数的几何意义:
几何意义:位于原点两侧且到原点距离相等的点所表示的两个数.2.观察下列各对有理数,从符号和绝对值方面你发现了什么?
5与-5; 2.5与-2.5;与与相反数的代数意义:
代数意义:符号不同、绝对值相同的两个数称作互为相反数,其中一个是另一个的相反数.解:符号不同、绝对值相同.
3.如何表示4,-3.5, 的相反数?
解:4的相反数为-4;-3.5的相反数为3.5;
的相反数为
相反数的表示:
(1)表示一个数(不是0)的相反数,可以再这个数的前面添一个“-”,即数a的相反数为-a.
(2)0的相反数是0.例2 求下列各数的相反数:
58,-4,3.14.解:58的相反数为-58;
-4的相反数为4;
3.14的相反数为-3.14.例3 填空:(1)3.5的相反数表示为 ;(2)-2.5的相反数表示为 ;(3)-(+4)是 的相反数;(4)-(-7)是 的相反数.-(-2.5)4-3.5-7思考:如何化简化简多重符号的方法:根据相反数的求法逐步由内向外化简.例4 化简:(1)-(+2.5)= ;(2)-(-2.5)= ;(3)+(-2.5)= ;(4)+(+2.5)= .-2.5-2.5+2.5+2.5三、绝对值的性质(1)绝对值是它本身的数是非负数,绝对值是它的相反数的数是非正数,0是绝对值最小的数.
(2)任何数都有且只有一个绝对值,任何数的绝对值都是非负数.
(3)绝对值是某个正数的数有两个,它们互为相反数.
(4)互为相反数的两个数的绝对值相等,反之,绝对值相等的两个数可能相等,也可能互为相反数.例2 比较-3与-6的大小.解:因为∣-3∣=3,∣-6∣=6,且3 < 6,
所以-3 > -6.四、利用绝对值比较数的大小法则:
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.比较-3,-0.4,-2的绝对值的大小,并用“<”把它们连接起来.练一练谈谈你这一节课有哪些收获.小结
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
