高中物理鲁科版课时作业波与相对论(选修3-4) 3 Word版含解析
文档属性
| 名称 | 高中物理鲁科版课时作业波与相对论(选修3-4) 3 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 520.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-09-16 09:06:38 | ||
图片预览




文档简介
课时作业3
一、光的折射和折射率
1.(2018洛阳校级月考)(多选)一束光从空气射向折射率n=的某种玻璃的表面,如图所示.i代表入射角,则( )
A.当入射角i=0°时不会发生折射现象
B.无论入射角i是多大,折射角r都不会超过45°
C.欲使折射角r=30°,应以i=60°的角度入射
D.当入射角i满足tan i=时,反射光线跟折射光线恰好互相垂直
BD 解析:当入射角i=0°时光能从空气进入玻璃,故发生了折射;当入射角是90°时,根据折射定律n=,解得r=45°,所以无论入射角i是多大,折射角r都不会超过45°;欲使折射角r=30°,根据折射定律n=,解得i=45°;当tan i=,根据折射定律n==tan i,解得sin r=cos i,所以反射光线跟折射光线恰好互相垂直.
2.(2018云南腾冲一模)(多选)如图所示,一细束红光与一细束蓝光平行射到同一个三棱镜上,经折射后交于光屏上的同一点M.若用n1和n2分别表示三棱镜对红光和蓝光的折射率,下列说法正确的是( )
A.n1>n2,a为蓝光,b为红光
B.n1<n2,a为蓝光,b为红光
C.a光在玻璃中的传播速度比b光小
D.a光在玻璃中的传播速度比b光大
E.a光的频率大于b光的频率
BCE 解析:由图看出,a光通过三棱镜后偏折角较大,根据折射定律得知三棱镜对a光的折射率较大,则知a为蓝光,b为红光,且有n1<n2,则a光的频率大于b光的频率;由公式v=分析可知a光在玻璃中的传播速度比b光小.
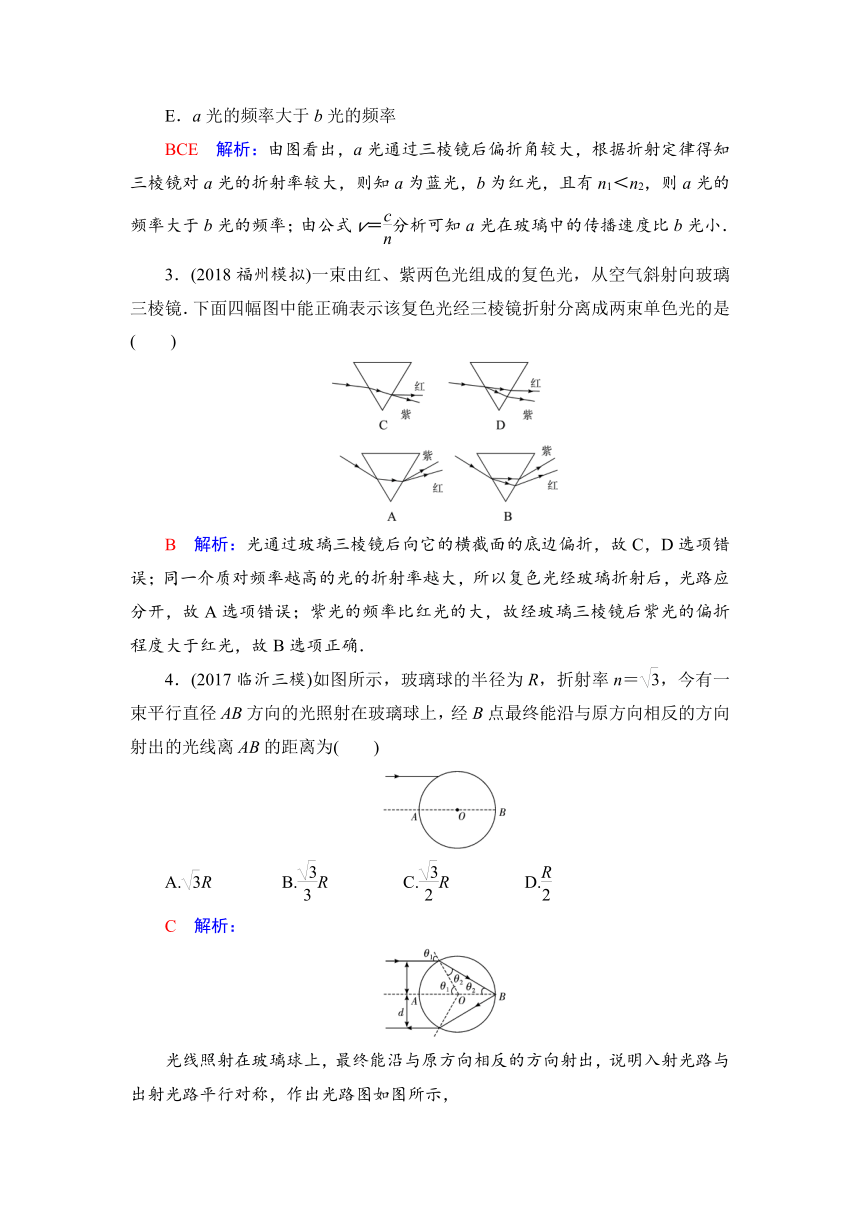
3.(2018福州模拟)一束由红、紫两色光组成的复色光,从空气斜射向玻璃三棱镜.下面四幅图中能正确表示该复色光经三棱镜折射分离成两束单色光的是( )
B 解析:光通过玻璃三棱镜后向它的横截面的底边偏折,故C,D选项错误;同一介质对频率越高的光的折射率越大,所以复色光经玻璃折射后,光路应分开,故A选项错误;紫光的频率比红光的大,故经玻璃三棱镜后紫光的偏折程度大于红光,故B选项正确.
4.(2017临沂三模)如图所示,玻璃球的半径为R,折射率n=,今有一束平行直径AB方向的光照射在玻璃球上,经B点最终能沿与原方向相反的方向射出的光线离AB的距离为( )
A.R B.R C.R D.
C 解析:
光线照射在玻璃球上,最终能沿与原方向相反的方向射出,说明入射光路与出射光路平行对称,作出光路图如图所示,
则θ1=2θ2,又由折射定律得n=,解得cos θ2=,即θ2=30°,θ1=60°,则d=Rsin θ1,所以d=R.
二、全反射
5.(2018蚌埠二模)光导纤维由很细的内芯和外套两层组成,内芯的折射率比外套大,光传播时在内芯和外套的界面发生全反射,如图所示.为了研究简单,现设外套为空气,内芯的折射率为n,一束光线由空气射入内芯,在内芯与空气的界面恰好发生全反射.若光速为c,则光线通过长度为L的光导纤维所用的时间为( )
A. B. C. D.
C 解析:设临界角为C,则光的传播方向与光导纤维的方向之间的夹角为(90°-C),光通过长度为L的光导纤维时的路程为s==,
光在光导纤维中的传播速度v=
又由于n=
所以光的传播时间t===.
6. (2017日照一模)一束白光从顶角为θ的三棱镜的一边以较大的入射角i射入并通过三棱镜后,在屏P上可得到彩色光带,如图所示,在入射角i逐渐减小到零的过程中,假如屏上的彩色光带先后全部消失,则( )
A.红光最先消失,紫光最后消失
B.紫光最先消失,红光最后消失
C.紫光最先消失,黄光最后消失
D.红光最先消失,黄光最后消失
B 解析:紫光的折射率最大,由sin C=,紫光的临界角最小,当入射角i逐渐减小到零的过程中,光线射到棱镜右侧面的入射角逐渐增大,紫光的入射角最先达到临界角,发生全反射,则紫光最先消失,红光最后消失.
三、光的折射和全反射的综合应用
7.
(2018洛阳校级月考)如图所示,扇形AOB为透明柱状介质的横截面,圆心角∠AOB=60°.一束平行于角平分线OM的单色光由OA射入介质,经OA折射的光线恰平行于OB,以下对该介质的折射率的值及折射光线中恰好射到M点的光线能不能发生全反射的说法正确的是( )
A.,不能发生全反射 B.,能发生全反射
C.,不能发生全反射 D.,能发生全反射
A 解析:
画出光路图,并根据几何关系标出角度,如图所示.由图可知,介质的折射率n==;因为sin 30°=<==sin C,所以折射光线中恰好射到M点的光线不能发生全反射.
8.[2017课标Ⅲ,34(2)]如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(ⅰ)从球面射出的光线对应的入射光线到光轴距离的最大值;
(ⅱ)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
解析:(ⅰ)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有
nsin ic=1②
由几何关系有
sin i=③
联立①②③式并利用题给条件,得
l=R④
(ⅱ)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsin i1=sin r1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
=⑥
由几何关系有
∠C=r1-i1⑦
sin i1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R⑨
答案:(ⅰ)R (ⅱ)R(或2.74R)
9.(2017天津和平质量调查,2)如图所示,OO′是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于OO′轴等距离且平行的两束不同单色细光束,从玻璃体射出后相交于OO′下方的P点,由此可以得出的结论是( )
A.在同种玻璃中传播,A光的传播速度一定大于B光
B.以相同角度斜射到同一玻璃板透过平行表面后,B光侧移量大
C.分别照射同一光电管,若B光能引起光电效应,A光一定也能
D.以相同的入射角从水中射入空气,在空气中只能看到一种光时,一定是A光
C 解析:由图可知A光的折射率nA大于B光的折射率nB,又由v=,可知vAvB,则以相同角度斜射到同一玻璃板透过平行表面后,A光侧移量大,B项错误.由于nA>nB,则vA>vB,若分别照射同一光电管,若B光能引起光电效应,A光一定也能,C项正确.在空气中只能看到一种光时,应是折射率较小的B光,D项错误.
【素能提升】
10.(2018全国2卷)如图,是一直角三棱镜的横截面,,,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
答案:(ⅰ)光线在BC面上折射,由折射定律有
sini1=nsinr1①
式中,n为棱镜的折射率,i1和r1分别是该光线在BC面上的入射角和折射角。光线在AC面上发生全反射,由反射定律有
i2=r2②
式中i2和r2分别是该光线在AC面上的入射角和反射角。光线在AB面上发生折射,由折射定律有
nsini3=sinr3③
式中i3和r3分别是该光线在AB面上的入射角和折射角。由几何关系得
i2=r2=60°,r1=i3=30°④
F点的出射光相对于D点的入射光的偏角为
δ=(r1–i1)+(180°–i2–r2)+(r3–i3)⑤
由①②③④⑤式得
δ=60°⑥
(ⅱ)光线在AC面上发生全反射,光线在AB面上不发生全反射,有
nsini2≥nsinC>nsini3⑦
式中C是全反射临界角,满足
nsinC=1⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为
≤n≤2⑨
11.(2017全国新课标理综Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
解析:设从光源发出直接射到D点的光线的入射角为i1,折射角为r1.在剖面内作光源相对于反光壁的镜像对称点C,连接C、D,交反光壁于E点,由光源射向E点的光线,反射后沿ED射向D点.光线在D点的入射角为i2,折射角为r2,如图所示.
设液体的折射率为n,由折射定律有
nsin i1=sin r1①
nsin i2=sin r2②
由题意知
r1+r2=90°③
联立①②③式得
n2=④
由几何关系可知
sin i1==⑤
sin i2==⑥
联立④⑤⑥式得n≈1.55⑦
答案:1.55
12.如图所示,某同学利用方格坐标纸测定半圆形玻璃砖的折射率,OA是画在纸上的直线,他在直线OA适当位置先后竖直插上P1,P2两枚大头针,如图放上玻璃砖(如粗黑线所示),然后插上P3,P4大头针.
(1)他确定P3大头针位置的方法应当是_____________.
(2)若该同学实验操作规范准确,其记录的情况如图所示.该同学还用圆规做了一个以O为圆心,半径与玻璃砖相同的半圆(如图中虚线所示).请您帮这位同学算出玻璃砖的折射率,写出必要的计算过程.
解析:(1)透过玻璃砖看,P3大头针挡住P1,P2两枚大头针的像.
(2)设每个方格的边长为1,如图,由折射定律可得:
n====1.5.
答案:见解析
13.(2018全国3卷)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点做AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察。恰好可以看到小标记的像;过O点做AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
解析:过D点作AB边的发现NN′,连接OD,则∠ODN=α为O点发出的光纤在D点的入射角;设该光线在D点的折射角为β,如图所示。根据折射定律有
nsinα=sinβ①
式中n为三棱镜的折射率
由几何关系可知
∠β=60°②
∠EOF=30°③
在ΔOEF中有
EF=OEsin∠EOF④
由③④式和题给条件得
OE=2cm⑤
根据题给条件可知,△OED为等腰三角形,有
α=30°⑥
由①②⑥式得
n=⑦
14.(2016全国卷Ⅰ)如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m.从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为.
(1)求池内的水深;
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m.当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°.求救生员的眼睛到池边的水平距离(结果保留1位有效数字).
解析:(1)如图,设到达池边的光线的入射角为i.依题意,水的折射率n=,光线的折射角θ=90°.由折射定律有nsin i=sin θ①
由几何关系有sin i=②
式中,l=3 m,h是池内水的深度.联立①②式并代入题给数据得
h= m≈2.6 m③
(2)设此时救生员的眼睛到池边的距离为x.依题意,救生员的视线与竖直方向的夹角为θ′=45°.由折射定律有nsin i′=sin θ′④
式中,i′是光线在水面的入射角.设池底点光源A到入射点的水平距离为a.由几何关系有
sin i′=⑤
x+l=a+h′⑥
式中h′=2 m.联立③④⑤⑥式得x=(3-1) m
≈0.7 m⑦
答案:(1)2.6 m (2)0.7 m
15.[2017江淮十校三模,34(2)]如图所示,在真空中有一个折射率为n、半径为r的质地均匀的小球.细激光束在真空中沿BC传播,BC与小球球心O的距离为l(l①光在C点发生折射的折射角的正弦值;
②细激光束在小球中传播的时间.
解析:①激光束两次折射的光路如图所示,按照光的折射定律有
n=
式中α与β分别是相应的入射角和折射角
由几何关系可知sin α=
解得sin β=
②根据n=,得v=
光在介质中传播的路径CD的长为s=2r cos β
光在小球内的传播时间Δt====
答案:① ②
解题关键:①正确作出光路图.②正确应用光的折射定律.③明确图中各角度之间的关系.④由几何关系求光传播的路程.⑤速度v=的应用.
16.[2017河北唐山一中模拟,34(2)]如图所示,在一厚度为d,折射率为n的大玻璃板下表面,有一半径为r的圆形发光面.已知真空中的光速为c.
①求从玻璃板上表面射出的光在玻璃中传播的最短时间tmin.
②为了从玻璃的上方看不见圆形发光面,在玻璃板的上表面贴有一块不透光的圆形纸片,求贴圆形纸片的最小面积Smin.
解析:①当光垂直于玻璃板的上下表面时,其在玻璃中传播的时间最短,有
tmin=,其中v=
解得tmin=
②设E为圆形发光面边缘上的一点,若由该点发出的光线恰好在玻璃的上表面D处发生全反射,则此光线的入射角等于临界角,如图所示,由几何关系有Δr=d tan C
又sin C=
解得Δr=
故所贴圆形纸片的最小半径为R=r+Δr
又Smin=πR2
解得Smin=π
答案:① ②π
一、光的折射和折射率
1.(2018洛阳校级月考)(多选)一束光从空气射向折射率n=的某种玻璃的表面,如图所示.i代表入射角,则( )
A.当入射角i=0°时不会发生折射现象
B.无论入射角i是多大,折射角r都不会超过45°
C.欲使折射角r=30°,应以i=60°的角度入射
D.当入射角i满足tan i=时,反射光线跟折射光线恰好互相垂直
BD 解析:当入射角i=0°时光能从空气进入玻璃,故发生了折射;当入射角是90°时,根据折射定律n=,解得r=45°,所以无论入射角i是多大,折射角r都不会超过45°;欲使折射角r=30°,根据折射定律n=,解得i=45°;当tan i=,根据折射定律n==tan i,解得sin r=cos i,所以反射光线跟折射光线恰好互相垂直.
2.(2018云南腾冲一模)(多选)如图所示,一细束红光与一细束蓝光平行射到同一个三棱镜上,经折射后交于光屏上的同一点M.若用n1和n2分别表示三棱镜对红光和蓝光的折射率,下列说法正确的是( )
A.n1>n2,a为蓝光,b为红光
B.n1<n2,a为蓝光,b为红光
C.a光在玻璃中的传播速度比b光小
D.a光在玻璃中的传播速度比b光大
E.a光的频率大于b光的频率
BCE 解析:由图看出,a光通过三棱镜后偏折角较大,根据折射定律得知三棱镜对a光的折射率较大,则知a为蓝光,b为红光,且有n1<n2,则a光的频率大于b光的频率;由公式v=分析可知a光在玻璃中的传播速度比b光小.
3.(2018福州模拟)一束由红、紫两色光组成的复色光,从空气斜射向玻璃三棱镜.下面四幅图中能正确表示该复色光经三棱镜折射分离成两束单色光的是( )
B 解析:光通过玻璃三棱镜后向它的横截面的底边偏折,故C,D选项错误;同一介质对频率越高的光的折射率越大,所以复色光经玻璃折射后,光路应分开,故A选项错误;紫光的频率比红光的大,故经玻璃三棱镜后紫光的偏折程度大于红光,故B选项正确.
4.(2017临沂三模)如图所示,玻璃球的半径为R,折射率n=,今有一束平行直径AB方向的光照射在玻璃球上,经B点最终能沿与原方向相反的方向射出的光线离AB的距离为( )
A.R B.R C.R D.
C 解析:
光线照射在玻璃球上,最终能沿与原方向相反的方向射出,说明入射光路与出射光路平行对称,作出光路图如图所示,
则θ1=2θ2,又由折射定律得n=,解得cos θ2=,即θ2=30°,θ1=60°,则d=Rsin θ1,所以d=R.
二、全反射
5.(2018蚌埠二模)光导纤维由很细的内芯和外套两层组成,内芯的折射率比外套大,光传播时在内芯和外套的界面发生全反射,如图所示.为了研究简单,现设外套为空气,内芯的折射率为n,一束光线由空气射入内芯,在内芯与空气的界面恰好发生全反射.若光速为c,则光线通过长度为L的光导纤维所用的时间为( )
A. B. C. D.
C 解析:设临界角为C,则光的传播方向与光导纤维的方向之间的夹角为(90°-C),光通过长度为L的光导纤维时的路程为s==,
光在光导纤维中的传播速度v=
又由于n=
所以光的传播时间t===.
6. (2017日照一模)一束白光从顶角为θ的三棱镜的一边以较大的入射角i射入并通过三棱镜后,在屏P上可得到彩色光带,如图所示,在入射角i逐渐减小到零的过程中,假如屏上的彩色光带先后全部消失,则( )
A.红光最先消失,紫光最后消失
B.紫光最先消失,红光最后消失
C.紫光最先消失,黄光最后消失
D.红光最先消失,黄光最后消失
B 解析:紫光的折射率最大,由sin C=,紫光的临界角最小,当入射角i逐渐减小到零的过程中,光线射到棱镜右侧面的入射角逐渐增大,紫光的入射角最先达到临界角,发生全反射,则紫光最先消失,红光最后消失.
三、光的折射和全反射的综合应用
7.
(2018洛阳校级月考)如图所示,扇形AOB为透明柱状介质的横截面,圆心角∠AOB=60°.一束平行于角平分线OM的单色光由OA射入介质,经OA折射的光线恰平行于OB,以下对该介质的折射率的值及折射光线中恰好射到M点的光线能不能发生全反射的说法正确的是( )
A.,不能发生全反射 B.,能发生全反射
C.,不能发生全反射 D.,能发生全反射
A 解析:
画出光路图,并根据几何关系标出角度,如图所示.由图可知,介质的折射率n==;因为sin 30°=<==sin C,所以折射光线中恰好射到M点的光线不能发生全反射.
8.[2017课标Ⅲ,34(2)]如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(ⅰ)从球面射出的光线对应的入射光线到光轴距离的最大值;
(ⅱ)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
解析:(ⅰ)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有
nsin ic=1②
由几何关系有
sin i=③
联立①②③式并利用题给条件,得
l=R④
(ⅱ)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsin i1=sin r1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
=⑥
由几何关系有
∠C=r1-i1⑦
sin i1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R⑨
答案:(ⅰ)R (ⅱ)R(或2.74R)
9.(2017天津和平质量调查,2)如图所示,OO′是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于OO′轴等距离且平行的两束不同单色细光束,从玻璃体射出后相交于OO′下方的P点,由此可以得出的结论是( )
A.在同种玻璃中传播,A光的传播速度一定大于B光
B.以相同角度斜射到同一玻璃板透过平行表面后,B光侧移量大
C.分别照射同一光电管,若B光能引起光电效应,A光一定也能
D.以相同的入射角从水中射入空气,在空气中只能看到一种光时,一定是A光
C 解析:由图可知A光的折射率nA大于B光的折射率nB,又由v=,可知vA
【素能提升】
10.(2018全国2卷)如图,是一直角三棱镜的横截面,,,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
答案:(ⅰ)光线在BC面上折射,由折射定律有
sini1=nsinr1①
式中,n为棱镜的折射率,i1和r1分别是该光线在BC面上的入射角和折射角。光线在AC面上发生全反射,由反射定律有
i2=r2②
式中i2和r2分别是该光线在AC面上的入射角和反射角。光线在AB面上发生折射,由折射定律有
nsini3=sinr3③
式中i3和r3分别是该光线在AB面上的入射角和折射角。由几何关系得
i2=r2=60°,r1=i3=30°④
F点的出射光相对于D点的入射光的偏角为
δ=(r1–i1)+(180°–i2–r2)+(r3–i3)⑤
由①②③④⑤式得
δ=60°⑥
(ⅱ)光线在AC面上发生全反射,光线在AB面上不发生全反射,有
nsini2≥nsinC>nsini3⑦
式中C是全反射临界角,满足
nsinC=1⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为
≤n≤2⑨
11.(2017全国新课标理综Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
解析:设从光源发出直接射到D点的光线的入射角为i1,折射角为r1.在剖面内作光源相对于反光壁的镜像对称点C,连接C、D,交反光壁于E点,由光源射向E点的光线,反射后沿ED射向D点.光线在D点的入射角为i2,折射角为r2,如图所示.
设液体的折射率为n,由折射定律有
nsin i1=sin r1①
nsin i2=sin r2②
由题意知
r1+r2=90°③
联立①②③式得
n2=④
由几何关系可知
sin i1==⑤
sin i2==⑥
联立④⑤⑥式得n≈1.55⑦
答案:1.55
12.如图所示,某同学利用方格坐标纸测定半圆形玻璃砖的折射率,OA是画在纸上的直线,他在直线OA适当位置先后竖直插上P1,P2两枚大头针,如图放上玻璃砖(如粗黑线所示),然后插上P3,P4大头针.
(1)他确定P3大头针位置的方法应当是_____________.
(2)若该同学实验操作规范准确,其记录的情况如图所示.该同学还用圆规做了一个以O为圆心,半径与玻璃砖相同的半圆(如图中虚线所示).请您帮这位同学算出玻璃砖的折射率,写出必要的计算过程.
解析:(1)透过玻璃砖看,P3大头针挡住P1,P2两枚大头针的像.
(2)设每个方格的边长为1,如图,由折射定律可得:
n====1.5.
答案:见解析
13.(2018全国3卷)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点做AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察。恰好可以看到小标记的像;过O点做AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
解析:过D点作AB边的发现NN′,连接OD,则∠ODN=α为O点发出的光纤在D点的入射角;设该光线在D点的折射角为β,如图所示。根据折射定律有
nsinα=sinβ①
式中n为三棱镜的折射率
由几何关系可知
∠β=60°②
∠EOF=30°③
在ΔOEF中有
EF=OEsin∠EOF④
由③④式和题给条件得
OE=2cm⑤
根据题给条件可知,△OED为等腰三角形,有
α=30°⑥
由①②⑥式得
n=⑦
14.(2016全国卷Ⅰ)如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m.从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为.
(1)求池内的水深;
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m.当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°.求救生员的眼睛到池边的水平距离(结果保留1位有效数字).
解析:(1)如图,设到达池边的光线的入射角为i.依题意,水的折射率n=,光线的折射角θ=90°.由折射定律有nsin i=sin θ①
由几何关系有sin i=②
式中,l=3 m,h是池内水的深度.联立①②式并代入题给数据得
h= m≈2.6 m③
(2)设此时救生员的眼睛到池边的距离为x.依题意,救生员的视线与竖直方向的夹角为θ′=45°.由折射定律有nsin i′=sin θ′④
式中,i′是光线在水面的入射角.设池底点光源A到入射点的水平距离为a.由几何关系有
sin i′=⑤
x+l=a+h′⑥
式中h′=2 m.联立③④⑤⑥式得x=(3-1) m
≈0.7 m⑦
答案:(1)2.6 m (2)0.7 m
15.[2017江淮十校三模,34(2)]如图所示,在真空中有一个折射率为n、半径为r的质地均匀的小球.细激光束在真空中沿BC传播,BC与小球球心O的距离为l(l
②细激光束在小球中传播的时间.
解析:①激光束两次折射的光路如图所示,按照光的折射定律有
n=
式中α与β分别是相应的入射角和折射角
由几何关系可知sin α=
解得sin β=
②根据n=,得v=
光在介质中传播的路径CD的长为s=2r cos β
光在小球内的传播时间Δt====
答案:① ②
解题关键:①正确作出光路图.②正确应用光的折射定律.③明确图中各角度之间的关系.④由几何关系求光传播的路程.⑤速度v=的应用.
16.[2017河北唐山一中模拟,34(2)]如图所示,在一厚度为d,折射率为n的大玻璃板下表面,有一半径为r的圆形发光面.已知真空中的光速为c.
①求从玻璃板上表面射出的光在玻璃中传播的最短时间tmin.
②为了从玻璃的上方看不见圆形发光面,在玻璃板的上表面贴有一块不透光的圆形纸片,求贴圆形纸片的最小面积Smin.
解析:①当光垂直于玻璃板的上下表面时,其在玻璃中传播的时间最短,有
tmin=,其中v=
解得tmin=
②设E为圆形发光面边缘上的一点,若由该点发出的光线恰好在玻璃的上表面D处发生全反射,则此光线的入射角等于临界角,如图所示,由几何关系有Δr=d tan C
又sin C=
解得Δr=
故所贴圆形纸片的最小半径为R=r+Δr
又Smin=πR2
解得Smin=π
答案:① ②π
同课章节目录
- 第1章 机械振动
- 导 入 从我国古代的“鱼洗”说起
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 生活中的振动
- 第2章 机械波
- 导 入 身边的波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第3章 电磁波
- 导 入 无处不在的电磁波
- 第1节 电磁波的产生
- 第2节 电磁波的发射、传播和接收
- 第3节 电磁波的应用及防护
- 专题探究 振动与波的实验与调研
- 第4章 光的折射与全反射
- 导 入 美妙的彩虹
- 第1节 光的折射定律
- 第2节 光的全反射
- 第3节 光导纤维及其应用
- 第5章 光的干涉 衍射 偏振
- 导 入 从五彩斑斓的肥皂泡说起
- 第1节 光的干涉
- 第2节 光的衍射
- 第3节 光的偏振
- 第4节 激光与全息照相
- 专题探究 光学部分的实验与调研
- 第6章 相对论与天体物理
- 导 入 从双生子佯谬谈起
- 第1节 牛顿眼中的世界
- 第2节 爱因斯坦眼中的世界
- 第3节 广义相对论初步
- 第4节 探索宇宙
