高中数学必修二教案 2. 2.4 平面与平面平行的性质
文档属性
| 名称 | 高中数学必修二教案 2. 2.4 平面与平面平行的性质 |
|
|
| 格式 | zip | ||
| 文件大小 | 84.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-16 19:26:58 | ||
图片预览


文档简介
集体备课电子教案
高一年级 数学备课组(总第 课时) 主备人: 时间: 年 月 日
课 题
2.2.4 平面与平面平行的性质
第8课时
教
学
目
标
1.理解平面与平面的性质定理的含义.
2.能用三种语言准确描述平面与平面的性质定理.
3.能用平面与平面的性质定理证明一些空间平行关系的简单命题.
教学重点
平面与平面平行的性质及应用.
教学难点
平面与平面平行性质定理的的探索过程及应用.
教学方法
引导发现法,采用以思导学的方式
教学过程:步骤、内容、教学活动
二次备课
【问题探究】
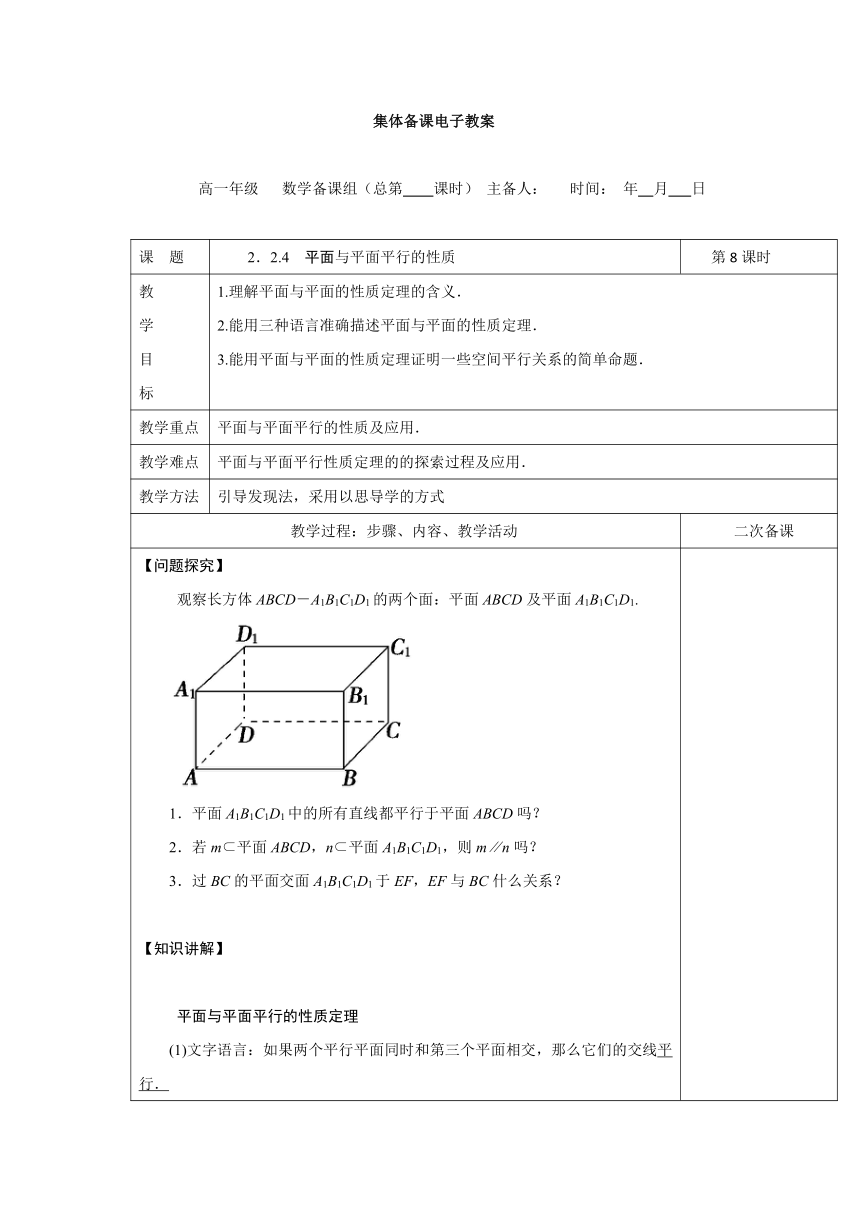
观察长方体ABCD-A1B1C1D1的两个面:平面ABCD及平面A1B1C1D1.
1.平面A1B1C1D1中的所有直线都平行于平面ABCD吗?
2.若m?平面ABCD,n?平面A1B1C1D1,则m∥n吗?
3.过BC的平面交面A1B1C1D1于EF,EF与BC什么关系?
【知识讲解】
平面与平面平行的性质定理
(1)文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
(2)符号语言:α∥β,α∩γ=a,β∩γ=b?a∥b.
(3)图形语言:如图所示.
(4)作用:证明两直线平行.
【知识运用】
?例1若平面α∥平面β,a?α,下列说法正确的是( )
①a与β内任一直线平行; ②a与β内无数条直线平行;
③a与β内任一直线不垂直; ④a与β无公共点.
A.①③ B.②④ C.②③ D.①③④
?课堂练习
a∥α,b∥β,α∥β,则a与b位置关系是( )
A.平行 B.异面
C.相交 D.平行或异面或相交
?例2如图,平面四边形ABCD的四个顶点A、B、C、D均在平行四边形A′B′C′D′所确定一个平面α外,且AA′、BB′、CC′、DD′互相平行.
求证:四边形ABCD是平行四边形.
?课堂练习
如图,已知α∥β,点P是平面α、β外的一点(不在α与β之间),直线PB、PD分别与α、β相交于点A、B和C、D.
(1)求证:AC∥BD;
(2)已知PA=4 cm,AB=5 cm,PC=3 cm,求PD的长.
【课堂小结】
1.三种平行关系可以任意转化,其相互转化关系如图所示:
2.证明线与线、线与面的平行关系的一般规律是:“见了已知想性质,见了求证想判定”,也就是说“发现已知,转化结论,沟通已知与未知的关系”.这是分析和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段.
【课外作业】
同步导练 第1--8题
板
书
设
计
教
学
反
思
高一年级 数学备课组(总第 课时) 主备人: 时间: 年 月 日
课 题
2.2.4 平面与平面平行的性质
第8课时
教
学
目
标
1.理解平面与平面的性质定理的含义.
2.能用三种语言准确描述平面与平面的性质定理.
3.能用平面与平面的性质定理证明一些空间平行关系的简单命题.
教学重点
平面与平面平行的性质及应用.
教学难点
平面与平面平行性质定理的的探索过程及应用.
教学方法
引导发现法,采用以思导学的方式
教学过程:步骤、内容、教学活动
二次备课
【问题探究】
观察长方体ABCD-A1B1C1D1的两个面:平面ABCD及平面A1B1C1D1.
1.平面A1B1C1D1中的所有直线都平行于平面ABCD吗?
2.若m?平面ABCD,n?平面A1B1C1D1,则m∥n吗?
3.过BC的平面交面A1B1C1D1于EF,EF与BC什么关系?
【知识讲解】
平面与平面平行的性质定理
(1)文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
(2)符号语言:α∥β,α∩γ=a,β∩γ=b?a∥b.
(3)图形语言:如图所示.
(4)作用:证明两直线平行.
【知识运用】
?例1若平面α∥平面β,a?α,下列说法正确的是( )
①a与β内任一直线平行; ②a与β内无数条直线平行;
③a与β内任一直线不垂直; ④a与β无公共点.
A.①③ B.②④ C.②③ D.①③④
?课堂练习
a∥α,b∥β,α∥β,则a与b位置关系是( )
A.平行 B.异面
C.相交 D.平行或异面或相交
?例2如图,平面四边形ABCD的四个顶点A、B、C、D均在平行四边形A′B′C′D′所确定一个平面α外,且AA′、BB′、CC′、DD′互相平行.
求证:四边形ABCD是平行四边形.
?课堂练习
如图,已知α∥β,点P是平面α、β外的一点(不在α与β之间),直线PB、PD分别与α、β相交于点A、B和C、D.
(1)求证:AC∥BD;
(2)已知PA=4 cm,AB=5 cm,PC=3 cm,求PD的长.
【课堂小结】
1.三种平行关系可以任意转化,其相互转化关系如图所示:
2.证明线与线、线与面的平行关系的一般规律是:“见了已知想性质,见了求证想判定”,也就是说“发现已知,转化结论,沟通已知与未知的关系”.这是分析和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段.
【课外作业】
同步导练 第1--8题
板
书
设
计
教
学
反
思
