高中数学必修二教案 2. 3.1 直线与平面垂直的判定
文档属性
| 名称 | 高中数学必修二教案 2. 3.1 直线与平面垂直的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 78.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-16 19:30:26 | ||
图片预览

文档简介
集体备课电子教案
高一年级 数学备课组(总第 课时) 主备人: 时间: 年 月 日
课 题
2.3.1 直线与平面垂直的判定
第9课时
教
学
目
标
1. 了解直线与平面垂直的定义.
2. 理解直线与平面垂直的判定定理,并会用其判断直线与平面垂直.
3. 理解直线与平面所成角的概念,并能解决简单的线面角问题.
教学重点
直线与平面垂直的定义和判定定理.
教学难点
操作确认并概括出直线与平面垂直的定义和判定定理.
教学方法
启发式和探究式
教学过程:步骤、内容、教学活动
二次备课
【问题探究】
1. 在阳光下观察直立于地面的旗杆及它在地面上的影子,随着时间的变化,影子的位置在移动,在各个时刻旗杆所在的直线与其影子所在的直线什么关系?
2. 将一块三角形纸片ABC沿折痕AD折起,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触).观察折痕AD与桌面的位置关系.
(1)折痕AD与桌面一定垂直吗?
(2)当折痕AD满足什么条件时,AD与桌面垂直?
【知识讲解】
1.直线与平面垂直的定义
文字语言
图形语言
符号语言
如果直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直, l叫做平面α的垂线,平面α叫做直线l的垂面,它们惟一的公共点P
叫做垂足
l⊥α
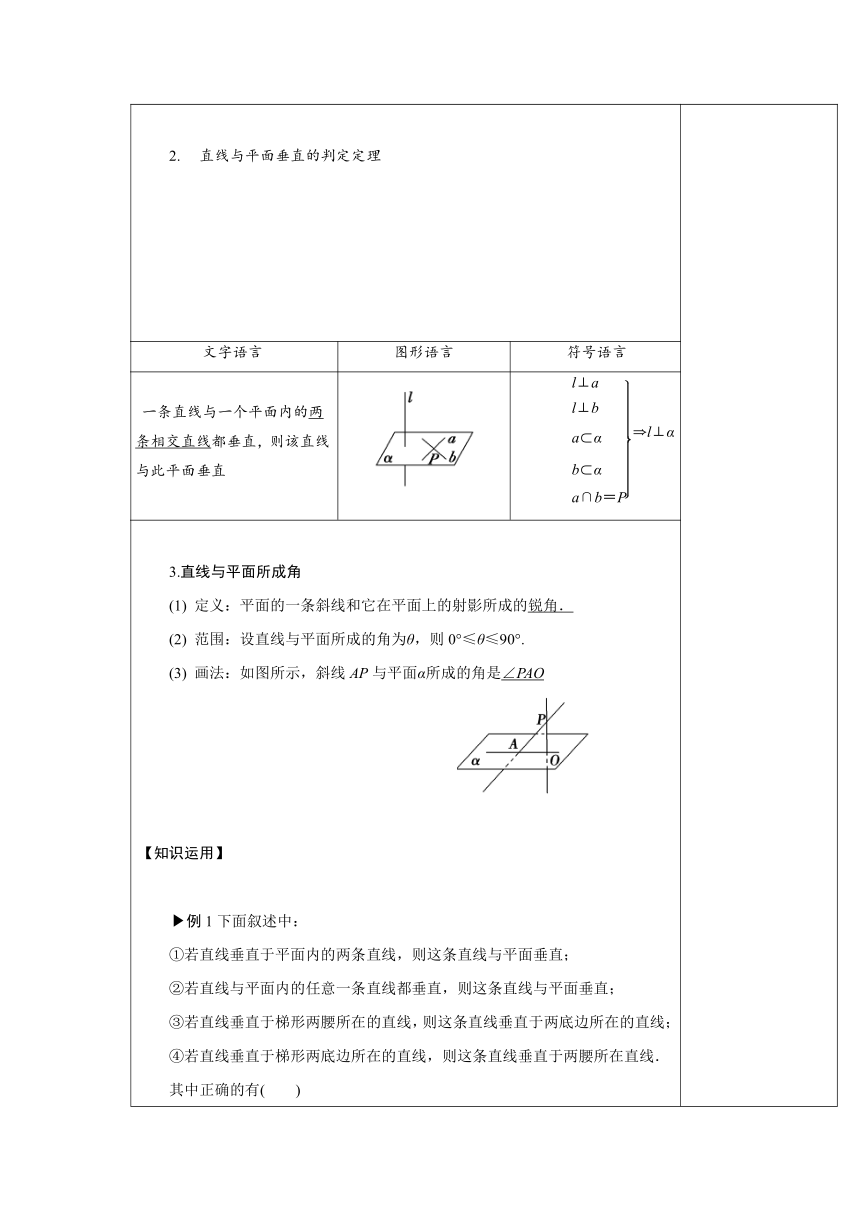
直线与平面垂直的判定定理
文字语言
图形语言
符号语言
直线与一个平面内的两条相交直线都垂直,则该直线
与此平面垂直
?l⊥α
3.直线与平面所成角
(1) 定义:平面的一条斜线和它在平面上的射影所成的锐角.
(2) 范围:设直线与平面所成的角为θ,则0°≤θ≤90°.
(3) 画法:如图所示,斜线AP与平面α所成的角是∠PAO
【知识运用】
?例1下面叙述中:
①若直线垂直于平面内的两条直线,则这条直线与平面垂直;
②若直线与平面内的任意一条直线都垂直,则这条直线与平面垂直;
③若直线垂直于梯形两腰所在的直线,则这条直线垂直于两底边所在的直线;④若直线垂直于梯形两底边所在的直线,则这条直线垂直于两腰所在直线.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
?课堂练习
有下列说法:
①如果一条直线和一个平面平行,那么它和这个平面内的任意直线都不垂直.
②如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
③过点A垂直于直线a的所有直线都在过点A且垂直于a的平面内.
其中错误的是( )
A.①② B.①③ C.②③ D.①②③
?例2 如图,已知△ABC中,∠ACB=90°,SA⊥平面ABC,AD⊥SC于D,求证:AD⊥平面SBC.
?课堂练习
如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心,求证:EF⊥平面BB1O.
?例3如图,在正方体ABCD—A1B1C1D1中,
(1)求A1B与平面AA1D1D所成的角;
(2)求A1B与平面BB1D1D所成的角.
?课堂练习
如图所示,Rt△BMC中,斜边BM=5,它在平面ABC上的射影AB长为4,∠MBC=60°,求MC与平面CAB所成角的正弦值.
【课堂小结】
1.线面垂直的定义具有双重性,既可以由线面垂直得出线线垂直,也可以由线线垂直得出线面垂直.
2.求线面角的关键是找直线在相应平面内的射影,并借助直角三角形的边角关系求线面角.
3.线线垂直和线面垂直体现了知识间的互化,在学习中体会等价转化思想.
【课外作业】
同步导练 第1--8题
板
书
设
计
教
学
反
思
高一年级 数学备课组(总第 课时) 主备人: 时间: 年 月 日
课 题
2.3.1 直线与平面垂直的判定
第9课时
教
学
目
标
1. 了解直线与平面垂直的定义.
2. 理解直线与平面垂直的判定定理,并会用其判断直线与平面垂直.
3. 理解直线与平面所成角的概念,并能解决简单的线面角问题.
教学重点
直线与平面垂直的定义和判定定理.
教学难点
操作确认并概括出直线与平面垂直的定义和判定定理.
教学方法
启发式和探究式
教学过程:步骤、内容、教学活动
二次备课
【问题探究】
1. 在阳光下观察直立于地面的旗杆及它在地面上的影子,随着时间的变化,影子的位置在移动,在各个时刻旗杆所在的直线与其影子所在的直线什么关系?
2. 将一块三角形纸片ABC沿折痕AD折起,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触).观察折痕AD与桌面的位置关系.
(1)折痕AD与桌面一定垂直吗?
(2)当折痕AD满足什么条件时,AD与桌面垂直?
【知识讲解】
1.直线与平面垂直的定义
文字语言
图形语言
符号语言
如果直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直, l叫做平面α的垂线,平面α叫做直线l的垂面,它们惟一的公共点P
叫做垂足
l⊥α
直线与平面垂直的判定定理
文字语言
图形语言
符号语言
直线与一个平面内的两条相交直线都垂直,则该直线
与此平面垂直
?l⊥α
3.直线与平面所成角
(1) 定义:平面的一条斜线和它在平面上的射影所成的锐角.
(2) 范围:设直线与平面所成的角为θ,则0°≤θ≤90°.
(3) 画法:如图所示,斜线AP与平面α所成的角是∠PAO
【知识运用】
?例1下面叙述中:
①若直线垂直于平面内的两条直线,则这条直线与平面垂直;
②若直线与平面内的任意一条直线都垂直,则这条直线与平面垂直;
③若直线垂直于梯形两腰所在的直线,则这条直线垂直于两底边所在的直线;④若直线垂直于梯形两底边所在的直线,则这条直线垂直于两腰所在直线.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
?课堂练习
有下列说法:
①如果一条直线和一个平面平行,那么它和这个平面内的任意直线都不垂直.
②如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.
③过点A垂直于直线a的所有直线都在过点A且垂直于a的平面内.
其中错误的是( )
A.①② B.①③ C.②③ D.①②③
?例2 如图,已知△ABC中,∠ACB=90°,SA⊥平面ABC,AD⊥SC于D,求证:AD⊥平面SBC.
?课堂练习
如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心,求证:EF⊥平面BB1O.
?例3如图,在正方体ABCD—A1B1C1D1中,
(1)求A1B与平面AA1D1D所成的角;
(2)求A1B与平面BB1D1D所成的角.
?课堂练习
如图所示,Rt△BMC中,斜边BM=5,它在平面ABC上的射影AB长为4,∠MBC=60°,求MC与平面CAB所成角的正弦值.
【课堂小结】
1.线面垂直的定义具有双重性,既可以由线面垂直得出线线垂直,也可以由线线垂直得出线面垂直.
2.求线面角的关键是找直线在相应平面内的射影,并借助直角三角形的边角关系求线面角.
3.线线垂直和线面垂直体现了知识间的互化,在学习中体会等价转化思想.
【课外作业】
同步导练 第1--8题
板
书
设
计
教
学
反
思
