高中数学必修二教案 第3章小结与复习
文档属性
| 名称 | 高中数学必修二教案 第3章小结与复习 | 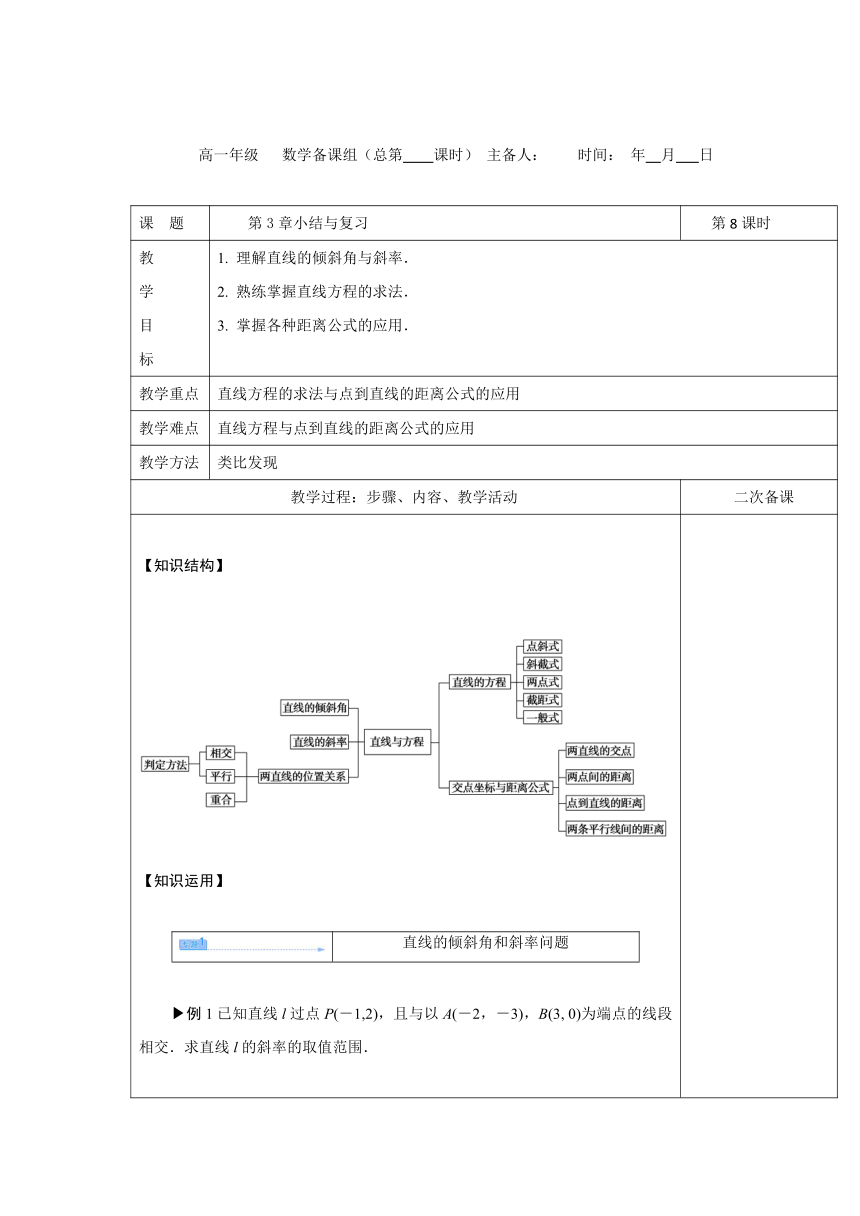 | |
| 格式 | zip | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-17 15:18:08 | ||
图片预览


文档简介
高一年级 数学备课组(总第 课时) 主备人: 时间: 年 月 日
课 题
第3章小结与复习
第8课时
教
学
目
标
1. 理解直线的倾斜角与斜率.
2. 熟练掌握直线方程的求法.
3. 掌握各种距离公式的应用.
教学重点
直线方程的求法与点到直线的距离公式的应用
教学难点
直线方程与点到直线的距离公式的应用
教学方法
类比发现
教学过程:步骤、内容、教学活动
二次备课
【知识结构】
【知识运用】
直线的倾斜角和斜率问题
?例1已知直线l过点P(-1,2),且与以A(-2,-3),B(3, 0)为端点的线段相交.求直线l的斜率的取值范围.
?课堂练习
已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
直线的方程
?例2 已知在第一象限的△ABC中,A(1,1),B(5,1),∠A=60°,∠B=45°,求:
(1)AB边所在直线的方程;
(2)AC边与BC边所在直线的方程.
?课堂练习
过点A(4,1)且在两坐标轴上的截距相等的直线方程是( )
A.x+y=5 B.x-y=5
C.x+y=5或x-4y=0 D.x-y=5或x+4y=0
直线的平行与垂直问题
?例3已知直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,求m的值,使得: (1)l1⊥l2; (2)l1∥l2.
?课堂练习
已知直线l的方程为3x+4y-12=0,分别求满足下列条件直线l′的方程.
(1)过点(-1,3),且与l平行;
(2)过点(-1,3),且与l垂直.
对称问题
?例4光线沿直线l1:x-2y+5=0射入,遇到直线l:3x-2y+7=0后反射,求反射光线所在的直线方程.
?课堂练习
求点A(2,2)关于直线2x-4y+9=0的对称点坐标.
分类讨论思想
?例5设直线l的方程为(a+1)x+y+2-a=0(a∈R)在两坐标轴上的截距相等,求直线l的方程.
?课堂练习
直线l经过点P(2,3),且在x,y轴上的截距互为相反数,试求该直线的方程.
【课堂小结】
1.倾斜角和斜率分别从“形”和“数”两个方面刻画了直线的倾斜程度.倾斜角α与斜率k的对应关系和单调性是解题的易错点,应引起特别重视.
2.直线方程的点斜式、斜截式、两点式、截距式都有各自的限制条件,不能表示所有的直线.直线方程的一般式则可以表示所有直线.在解题的时候,如果没有特别说明,最后的结果都要化成一般式.
3. 利用直线的方程判定两条直线的平行或垂直关系是这部分知识常涉及的题型.求解时,可以利用斜率之间的关系判定;若方程都是一般式,知道平行或垂直关系,求参数的值时也可用如下方法:
直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.
(1)l1∥l2时,可令A1B2-A2B1=0,解得参数的值后,再代入方程验证,排除重合的情况;
(2)l1⊥l2时,可利用A1A2+B1B2=0直接求参数的值.
【课外作业】
教材 A组 第1--12题
板
书
设
计
教
学
反
思
