人教A版高中数学必修五教案 3.3.2 简单的线性规划问题
文档属性
| 名称 | 人教A版高中数学必修五教案 3.3.2 简单的线性规划问题 |  | |
| 格式 | zip | ||
| 文件大小 | 79.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-17 16:04:23 | ||
图片预览


文档简介
3.3.2简单的线性规划问题
一、教学背景
1.本节课是《普通高中课程标准实验教科书数学》人教A版必修5第三章《不等式》中3.3.2《简单的线性规划问题》的第一课时。主要内容是线性规划的相关概念和简单的线性规划问题的解法。
2.本节课的教学对象是河北省秦皇岛市抚宁区第一中学高一文班学生。
二、教学目标
(一)知识与技能
1.?了解约束条件、目标函数、可行解、可行域、最优解等基本概念。
2.?会用图解法解决简单线性规划问题,即求目标函数的最大值或最小值。
(二)过程与方法
在线性规划问题的探究过程中,引导学生通过观察、分析、操作、归纳、概括的基本环节,达到知识的建构。增强学生的观察、联想、细心作图的能力,把握化归思想和数形结合两大数学思想。
注重培养学生积极主动、勇于探索的学习方式,整节课着重创造师生互动、生生互动的良好学习环境,学生在老师的引导下亲身经历动手实践、动脑思考等方法探究线性规划的简单问题获取直接结题经验。
(三)情感态度与价值观
学习中渗透函数、数形结合、化归等重要数学思想,培养学生“数形结合”的应用数学的意识,激发学生的学习兴趣。
结合本节教学内容,让学生成为课堂活动的主导,体验探究学习、合作学习的乐趣,并从中获得成功的体验,增强学生学习数学知识的自信心。培养实事求是、理论与实际相结合的科学态度和科学道德。
三、教学重点和难点
教学重点:图解法解线性规划问题。
教学难点:准确求得线性规划问题的最优解。
四、教学过程
(一)复习回顾
在同一坐标系上作出下列直线:;;;;。
投影展示学生的画图作业,引导学生观察5条直线的特征:平行。
得出结论:形如的直线与平行。
直线中的叫做纵截距:直线与轴交点的纵坐标。
(二)学习新知
老师:上一节课我们学习了二元一次不等式组和平面区域,这节课咱们接着往下学习。
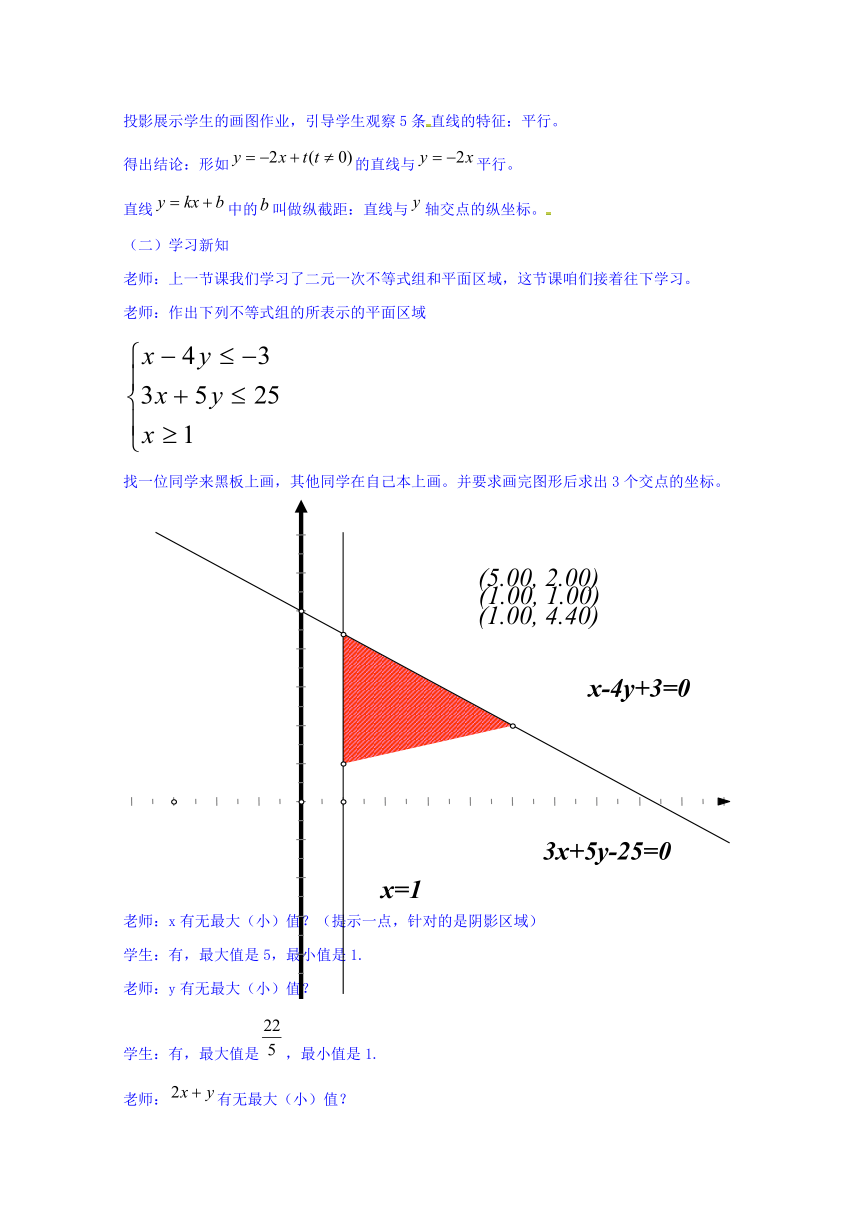
老师:作出下列不等式组的所表示的平面区域
找一位同学来黑板上画,其他同学在自己本上画。并要求画完图形后求出3个交点的坐标。
老师:x有无最大(小)值?(提示一点,针对的是阴影区域)
学生:有,最大值是5,最小值是1.
老师:y有无最大(小)值?
学生:有,最大值是,最小值是1.
老师:有无最大(小)值?
学生:有…
老师:很多学生也说有,但是到底是多少我们现在还不知道。这也是我们这节课要学习的内容。首先我们借助这道题目强调几个概念。
(1)线性约束条件:在上述问题中,不等式组是一组变量的约束条件,这组约束条件都是关于的一次不等式,故又称线性约束条件.
(2)线性目标函数:关于的一次式是欲达到最大值或最小值所涉及的变量的解析式,叫线性目标函数。
(3)线性规划问题:一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题。
(4)可行解、可行域和最优解:满足线性约束条件的解叫可行解;由所有可行解组成的集合叫做可行域;使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。
老师:这就是这节课要讲的简单的线性规划问题(并板书标题)。
老师:将(1)看作是直线l的方程,那么z有什么几何意义?
学生:化成,发现z就是b。
老师:那b具有什么样的几何意义来着?
学生:与y轴交点的纵坐标。
老师:把求z的最值问题转化成求对应直线与y轴交点的纵坐标的最值。我们发现与谁平行?
学生:。
老师:引导学生找两点在黑板上画出该直线。
老师:平行移动使学生自己顺利的说出在A点取最小值,在B点取最大值。
老师:画出过A点的直线,强调其与y轴交点的纵坐标就是z的最小值。画出过B点的直线,强调其与y轴交点的纵坐标就是z的最大值。
老师:规范思路,单独叫学生回答问题。
老师:做题一共分几步?
学生:画(求交点)、移、求、答。
规律总结:设计第(1)问意在展示解决一般线性规划问题的方法和基本步骤。图解法是解决线性规划问题的有效方法,其重点是利用z的几何意义求解。平行移动直线()时,看最先接触可行域和最后离开可行域时它经过的是哪个点(哪些点),那么这样的点就是最优解,最优解一般是在可行域的边界处取得。
老师:约束条件不变,目标函数改为(2)?(给学生思考时间,易错题)
老师:首先我们把化成?
学生:。
老师:与上一个目标函数对比,-z容易出错误。
老师:是?
学生:。
老师:引导学生找两点画出该直线,虚线表示。
老师:平行移动往上移动经过?
学生:C点。
老师:直线最高纵截距最大,也是-z?
学生:最大。
老师:-z最大也是z?
学生:最小。
规律总结:设计第(2)问意在提醒学生,解线性规划问题时,一定要判断最优解的对应点是最大值点,还是最小值点。对于目标函数,当时,直线截距最大时,有最大值,截距最小时,有最小值;当时,则相反。
老师:约束条件不变,目标函数再改为(3)?(给学生思考时间)
老师:变形?
学生:。
老师:?
学生:。
老师:过哪两个点?
学生:
老师:画出来的直线有什么特征?
学生:与BC平行。
老师:平行移动,最开始经过?
学生:A.
老师:经过A,z取得最?
学生:最大值。
老师:继续移动,与BC?
学生:重合时,取得最大值?
老师:最优解是?
学生:BC线段上所有的点。
规律总结:设计第(3)问的目的是在提醒学生,最优解不一定是一个,有时最优解有多个,或者无数个。本例最优解对应的最大值点就有无数个。
五、课堂小结
老师:找同学说说这节课我们学习了什么内容?
学生:几个概念,做线性规划题目的步骤。
老师帮助幻灯片展示:
解线性规划题目的一般步骤:
画:准确画出题目当中线性约束条件所表示的可行域;
移:在线性目标函数所表示的一组平行线中,通过平移发现与可行域有公共点且纵截距最大或最小的直线;
求:通过联立两条直线的方程解方程组求出最优解;
答。
板书设计
3.3.2简单线性规划问题
(1)(2)(3)
七、教学反思
求得线性规划最优解的方法是精确作图,借助数形结合将代数问题几何化。本节教学应引导学生准确把握集合、函数、化归、数形结合等数学思想方法,将实际问题数学化,代数问题几何化。为3.3.2简单线性规划问题(第二课时)线性规划在实际生活中的应用做铺垫。
一、教学背景
1.本节课是《普通高中课程标准实验教科书数学》人教A版必修5第三章《不等式》中3.3.2《简单的线性规划问题》的第一课时。主要内容是线性规划的相关概念和简单的线性规划问题的解法。
2.本节课的教学对象是河北省秦皇岛市抚宁区第一中学高一文班学生。
二、教学目标
(一)知识与技能
1.?了解约束条件、目标函数、可行解、可行域、最优解等基本概念。
2.?会用图解法解决简单线性规划问题,即求目标函数的最大值或最小值。
(二)过程与方法
在线性规划问题的探究过程中,引导学生通过观察、分析、操作、归纳、概括的基本环节,达到知识的建构。增强学生的观察、联想、细心作图的能力,把握化归思想和数形结合两大数学思想。
注重培养学生积极主动、勇于探索的学习方式,整节课着重创造师生互动、生生互动的良好学习环境,学生在老师的引导下亲身经历动手实践、动脑思考等方法探究线性规划的简单问题获取直接结题经验。
(三)情感态度与价值观
学习中渗透函数、数形结合、化归等重要数学思想,培养学生“数形结合”的应用数学的意识,激发学生的学习兴趣。
结合本节教学内容,让学生成为课堂活动的主导,体验探究学习、合作学习的乐趣,并从中获得成功的体验,增强学生学习数学知识的自信心。培养实事求是、理论与实际相结合的科学态度和科学道德。
三、教学重点和难点
教学重点:图解法解线性规划问题。
教学难点:准确求得线性规划问题的最优解。
四、教学过程
(一)复习回顾
在同一坐标系上作出下列直线:;;;;。
投影展示学生的画图作业,引导学生观察5条直线的特征:平行。
得出结论:形如的直线与平行。
直线中的叫做纵截距:直线与轴交点的纵坐标。
(二)学习新知
老师:上一节课我们学习了二元一次不等式组和平面区域,这节课咱们接着往下学习。
老师:作出下列不等式组的所表示的平面区域
找一位同学来黑板上画,其他同学在自己本上画。并要求画完图形后求出3个交点的坐标。
老师:x有无最大(小)值?(提示一点,针对的是阴影区域)
学生:有,最大值是5,最小值是1.
老师:y有无最大(小)值?
学生:有,最大值是,最小值是1.
老师:有无最大(小)值?
学生:有…
老师:很多学生也说有,但是到底是多少我们现在还不知道。这也是我们这节课要学习的内容。首先我们借助这道题目强调几个概念。
(1)线性约束条件:在上述问题中,不等式组是一组变量的约束条件,这组约束条件都是关于的一次不等式,故又称线性约束条件.
(2)线性目标函数:关于的一次式是欲达到最大值或最小值所涉及的变量的解析式,叫线性目标函数。
(3)线性规划问题:一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题。
(4)可行解、可行域和最优解:满足线性约束条件的解叫可行解;由所有可行解组成的集合叫做可行域;使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。
老师:这就是这节课要讲的简单的线性规划问题(并板书标题)。
老师:将(1)看作是直线l的方程,那么z有什么几何意义?
学生:化成,发现z就是b。
老师:那b具有什么样的几何意义来着?
学生:与y轴交点的纵坐标。
老师:把求z的最值问题转化成求对应直线与y轴交点的纵坐标的最值。我们发现与谁平行?
学生:。
老师:引导学生找两点在黑板上画出该直线。
老师:平行移动使学生自己顺利的说出在A点取最小值,在B点取最大值。
老师:画出过A点的直线,强调其与y轴交点的纵坐标就是z的最小值。画出过B点的直线,强调其与y轴交点的纵坐标就是z的最大值。
老师:规范思路,单独叫学生回答问题。
老师:做题一共分几步?
学生:画(求交点)、移、求、答。
规律总结:设计第(1)问意在展示解决一般线性规划问题的方法和基本步骤。图解法是解决线性规划问题的有效方法,其重点是利用z的几何意义求解。平行移动直线()时,看最先接触可行域和最后离开可行域时它经过的是哪个点(哪些点),那么这样的点就是最优解,最优解一般是在可行域的边界处取得。
老师:约束条件不变,目标函数改为(2)?(给学生思考时间,易错题)
老师:首先我们把化成?
学生:。
老师:与上一个目标函数对比,-z容易出错误。
老师:是?
学生:。
老师:引导学生找两点画出该直线,虚线表示。
老师:平行移动往上移动经过?
学生:C点。
老师:直线最高纵截距最大,也是-z?
学生:最大。
老师:-z最大也是z?
学生:最小。
规律总结:设计第(2)问意在提醒学生,解线性规划问题时,一定要判断最优解的对应点是最大值点,还是最小值点。对于目标函数,当时,直线截距最大时,有最大值,截距最小时,有最小值;当时,则相反。
老师:约束条件不变,目标函数再改为(3)?(给学生思考时间)
老师:变形?
学生:。
老师:?
学生:。
老师:过哪两个点?
学生:
老师:画出来的直线有什么特征?
学生:与BC平行。
老师:平行移动,最开始经过?
学生:A.
老师:经过A,z取得最?
学生:最大值。
老师:继续移动,与BC?
学生:重合时,取得最大值?
老师:最优解是?
学生:BC线段上所有的点。
规律总结:设计第(3)问的目的是在提醒学生,最优解不一定是一个,有时最优解有多个,或者无数个。本例最优解对应的最大值点就有无数个。
五、课堂小结
老师:找同学说说这节课我们学习了什么内容?
学生:几个概念,做线性规划题目的步骤。
老师帮助幻灯片展示:
解线性规划题目的一般步骤:
画:准确画出题目当中线性约束条件所表示的可行域;
移:在线性目标函数所表示的一组平行线中,通过平移发现与可行域有公共点且纵截距最大或最小的直线;
求:通过联立两条直线的方程解方程组求出最优解;
答。
板书设计
3.3.2简单线性规划问题
(1)(2)(3)
七、教学反思
求得线性规划最优解的方法是精确作图,借助数形结合将代数问题几何化。本节教学应引导学生准确把握集合、函数、化归、数形结合等数学思想方法,将实际问题数学化,代数问题几何化。为3.3.2简单线性规划问题(第二课时)线性规划在实际生活中的应用做铺垫。
