2.3 绝对值 课件
图片预览






文档简介
(共26张PPT)
数学北师大版
七年级上
第二章 有理数及其运算
3. 绝对值
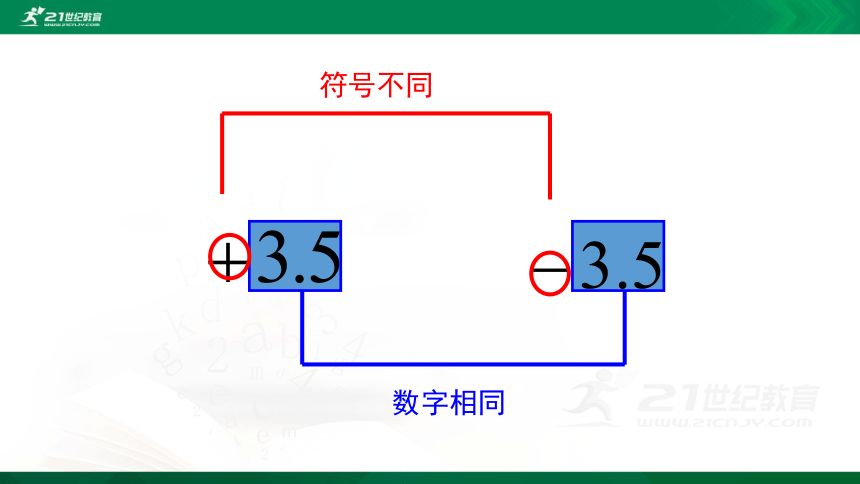
思考:+3与-3,-5与+5,-1.5与1.5这三对数有什么共同点和不同点?
数字相同
符号不同
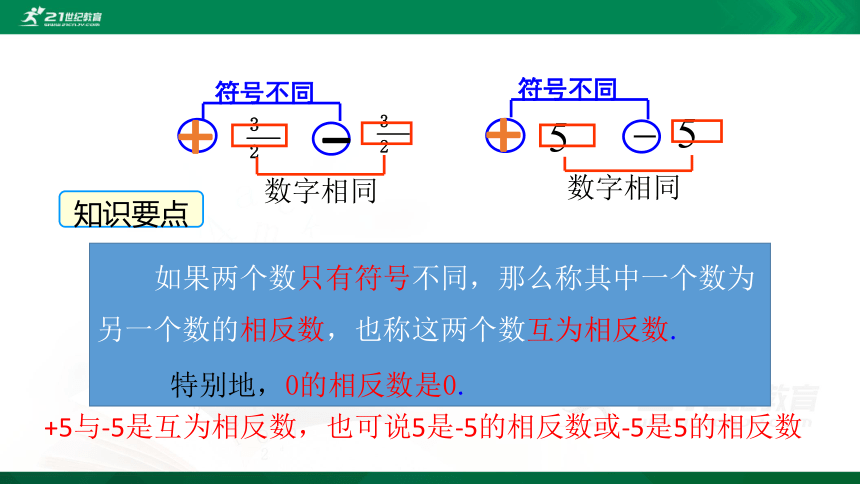
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.
特别地,0的相反数是0.
数字相同
符号不同
+
-
数字相同
符号不同
+
知识要点
+5与-5是互为相反数,也可说5是-5的相反数或-5是5的相反数
练一练
判断题,看谁回答的又对又快!
(1)-10是10的相反数( )
(2)10是10的相反数( )
(3)1.5与-1.5互为相反数( )
(4)-2是相反数 ( )
×
√
√
×
练一练
以下各数它们的相反数是什么?
-1, 0, , -400, +0.888 ,2019
答: , , , , ,
1
0
-
400
-0.888
-2019
-7.2是7.2的相反数。那么-(-7.2)是多少呢?运用相反数的知识解答
解:-(-7.2)可以看作是-7.2的相反数,故得到7.2。
总结规律:二个负号得到正号,可以说是“负负得正”
注意:二个符号在一起必须用括号-(-0.5)
而不能写成- -0.5
×
求一个数的相反数只要在前面加上一个负号即可。
如8.2的相反数就是
8.2
-
再如-2.7的相反数是
即2.7
-(-2.7)
二个符号在一起必须用括号
那么a的相反数是多少?-b的相反数又是什么?
a的相反数是-a
-b的相反数b
-(-2.7)=2.7
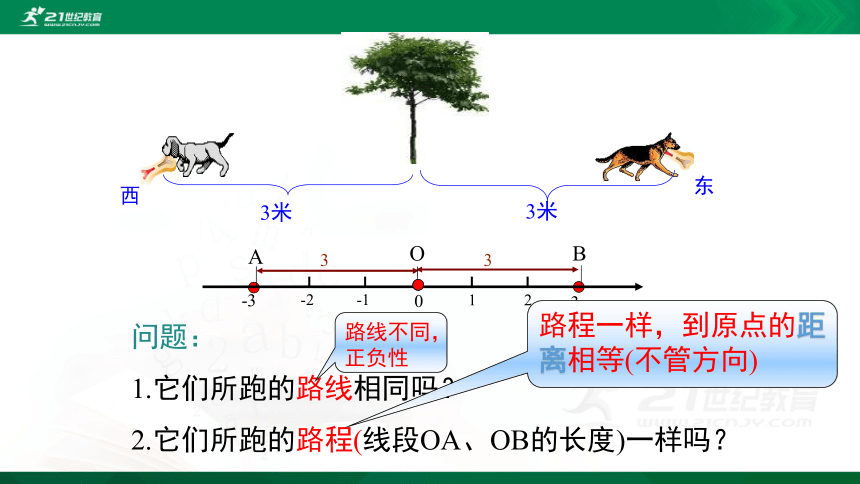
问题:
1.它们所跑的路线相同吗?
2.它们所跑的路程(线段OA、OB的长度)一样吗?
西
东
3米
3米
3
3
A
O
B
0
3
-3
1
2
-2
-1
路线不同,正负性
路程一样,到原点的距离相等(不管方向)
观察下图,回答问题:
3和-3互为相反数所对应的点在数轴上的位置有什么关系?
0
1
2
3
4
-1
-2
-3
5
在数轴上,表示互为相反数的两个点,位于原点的两侧,且与原点的距离相等。
练一练,在下图中画出点a的相反数的点来
0
a
-a
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
知识要点
请问到原点的距离为3个单位长度的点表示什么数?
互为相反数的绝对值有什么关系:
“+3的绝对值等于3”用数学符号表示为:
-3的绝对值呢?
0的绝对值呢?
│+3│=3
│-3│=3
│0│=0
0
1
2
3
4
-1
-2
-3
5
互为相反数的绝对值相等
想一想
如果a表示有理数,那么│a│有什么含义?
答: |a|表示数a的绝对值;
|a|表示数轴上数a对应的点与原点的距离.
一个字母可以表示任意有理数,即可以是正数,也可以是负数。这里的a即可代表正数,也可代表负数也可代表0
议一议
1.怎样表示a的相反数?
2.互为相反数的两个数的绝对值又有什么关系呢?
a
-a
相反数
|a|= |-a|
3.若:|a|= |b|,则:a与b有什么关系?
a=b
a=-b
4.你理解上面的“符号后的‘数’ 相同”的意思了吗?
例1、求下列各数的绝对值 :
- 7.8, 7.8, - 21, 21,- , , 0
解: | -7.8 | = 7.8;
议一议:互为相反数的两个数的绝对值有什么关系?
一个数的绝对值与这个数有什么关系?
| 7.8 | = 7.8;
| - 21| = 21 ;
| 21 | = 21 ;
| - | = ;
| | = ;
| 0 | = 0.
思考:-21=21对吗?∣-21∣是负数吗?
注意绝对值的符号不能忘记写了
我发现:互为相反数的两个数的绝对值相等.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
例 比较-1和–5的大小:
解: (利用数轴比较两个负数的大小)如图
0
1
2
3
-1
-2
-3
-4
-5
因为- 5在–1左边,所以 - 5﹤ - 1 ;
再看 | -1| = 1, | -5 | = 5 ,
而 - 1> - 5 .
由此二个负数比较大小,用绝对值来比较可得出什么结论,
负数比较大小,绝对值大的反而小
例 比较下列每组数的大小:
(1) -1和–5; (2)- 和- 2.7 .
解法一(利用绝对值比较两个负数的大小)
解:(1) ∵ | -1| = 1, | -5 | = 5 ,
1﹤5,
∴ - 1> - 5 .
(2)∵ | - | = , |- 2.7| =2.7,
﹤2.7,
∴ - ﹥-2.7
解法二 (利用数轴比较两个负数的大小)如图
0
1
2
3
-1
-2
-3
-4
-5
因为- 5在–1左边,所以 - 5﹤ - 1 ;
0
1
2
3
-1
-2
-3
-4
-5
-2.7
-
因为- 2.7在 - 的左边,所以- 2.7﹤ -
1.在数轴上距离原点2个单位长度的点表示的数是___,也就是说绝对值等于2的数是___ .
2和-2,也可合起来写 +2
2.在数轴上表示下列各数,并求它们的绝对值:
, 6 , -3 ,
3.比较下列各组数的大小:
(1) (2)
(3) (4)
4.下面的说法是否正确?请将错误的改正过来.
(1)有理数的绝对值一定比0大;
(2)有理数的相反数一定比0小;
(3)如果两个数的绝对值相等,那么这两个数相等;
(4)互为相反数的两个数的绝对值相等.
(5)字母a表示一个有理数那么-a是负数。
可以等于0
可以是正数,0和负数
还有可能是互为相反数
-a可以是正数,0和负数
1.相反数:如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数。
0的相反数是0
a的相反数是-a
2.绝对值:在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.
一个数 的绝对值记作:│ │
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0 的绝对值是 0.
互为相反数的两个数的绝对值相等.
任何一个有理数的绝对值都是 .
非负数
3.会用绝对值比较两个负数的大小:
两个负数比较大小,绝对值大的反而小.
当堂检测
1. │-5│= , │+3│= ,│0│= .
2.一个数的绝对值是它本身,那么这个数一定是
__________________。
3.用“>、<、=”号填空
│+8│ │-8│ , -5 -8. -4____8
4.如果一个数的绝对值等于 4,那么这个数等于__________.
5.绝对值小于3的整数有___个,分别是 ______________.
1、 某日上午,出租车司机小李在南北走向的商业大道上运营,如果规定向北为正,向南为负,出租车的行车里程如下(单位:km):
-17,-4,+13,-10,-12,+3,-13,+15,+20.
若每千米耗油0.2升,则这天上午该出租车共耗油多少升?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
七年级上
第二章 有理数及其运算
3. 绝对值
思考:+3与-3,-5与+5,-1.5与1.5这三对数有什么共同点和不同点?
数字相同
符号不同
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.
特别地,0的相反数是0.
数字相同
符号不同
+
-
数字相同
符号不同
+
知识要点
+5与-5是互为相反数,也可说5是-5的相反数或-5是5的相反数
练一练
判断题,看谁回答的又对又快!
(1)-10是10的相反数( )
(2)10是10的相反数( )
(3)1.5与-1.5互为相反数( )
(4)-2是相反数 ( )
×
√
√
×
练一练
以下各数它们的相反数是什么?
-1, 0, , -400, +0.888 ,2019
答: , , , , ,
1
0
-
400
-0.888
-2019
-7.2是7.2的相反数。那么-(-7.2)是多少呢?运用相反数的知识解答
解:-(-7.2)可以看作是-7.2的相反数,故得到7.2。
总结规律:二个负号得到正号,可以说是“负负得正”
注意:二个符号在一起必须用括号-(-0.5)
而不能写成- -0.5
×
求一个数的相反数只要在前面加上一个负号即可。
如8.2的相反数就是
8.2
-
再如-2.7的相反数是
即2.7
-(-2.7)
二个符号在一起必须用括号
那么a的相反数是多少?-b的相反数又是什么?
a的相反数是-a
-b的相反数b
-(-2.7)=2.7
问题:
1.它们所跑的路线相同吗?
2.它们所跑的路程(线段OA、OB的长度)一样吗?
西
东
3米
3米
3
3
A
O
B
0
3
-3
1
2
-2
-1
路线不同,正负性
路程一样,到原点的距离相等(不管方向)
观察下图,回答问题:
3和-3互为相反数所对应的点在数轴上的位置有什么关系?
0
1
2
3
4
-1
-2
-3
5
在数轴上,表示互为相反数的两个点,位于原点的两侧,且与原点的距离相等。
练一练,在下图中画出点a的相反数的点来
0
a
-a
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
知识要点
请问到原点的距离为3个单位长度的点表示什么数?
互为相反数的绝对值有什么关系:
“+3的绝对值等于3”用数学符号表示为:
-3的绝对值呢?
0的绝对值呢?
│+3│=3
│-3│=3
│0│=0
0
1
2
3
4
-1
-2
-3
5
互为相反数的绝对值相等
想一想
如果a表示有理数,那么│a│有什么含义?
答: |a|表示数a的绝对值;
|a|表示数轴上数a对应的点与原点的距离.
一个字母可以表示任意有理数,即可以是正数,也可以是负数。这里的a即可代表正数,也可代表负数也可代表0
议一议
1.怎样表示a的相反数?
2.互为相反数的两个数的绝对值又有什么关系呢?
a
-a
相反数
|a|= |-a|
3.若:|a|= |b|,则:a与b有什么关系?
a=b
a=-b
4.你理解上面的“符号后的‘数’ 相同”的意思了吗?
例1、求下列各数的绝对值 :
- 7.8, 7.8, - 21, 21,- , , 0
解: | -7.8 | = 7.8;
议一议:互为相反数的两个数的绝对值有什么关系?
一个数的绝对值与这个数有什么关系?
| 7.8 | = 7.8;
| - 21| = 21 ;
| 21 | = 21 ;
| - | = ;
| | = ;
| 0 | = 0.
思考:-21=21对吗?∣-21∣是负数吗?
注意绝对值的符号不能忘记写了
我发现:互为相反数的两个数的绝对值相等.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
例 比较-1和–5的大小:
解: (利用数轴比较两个负数的大小)如图
0
1
2
3
-1
-2
-3
-4
-5
因为- 5在–1左边,所以 - 5﹤ - 1 ;
再看 | -1| = 1, | -5 | = 5 ,
而 - 1> - 5 .
由此二个负数比较大小,用绝对值来比较可得出什么结论,
负数比较大小,绝对值大的反而小
例 比较下列每组数的大小:
(1) -1和–5; (2)- 和- 2.7 .
解法一(利用绝对值比较两个负数的大小)
解:(1) ∵ | -1| = 1, | -5 | = 5 ,
1﹤5,
∴ - 1> - 5 .
(2)∵ | - | = , |- 2.7| =2.7,
﹤2.7,
∴ - ﹥-2.7
解法二 (利用数轴比较两个负数的大小)如图
0
1
2
3
-1
-2
-3
-4
-5
因为- 5在–1左边,所以 - 5﹤ - 1 ;
0
1
2
3
-1
-2
-3
-4
-5
-2.7
-
因为- 2.7在 - 的左边,所以- 2.7﹤ -
1.在数轴上距离原点2个单位长度的点表示的数是___,也就是说绝对值等于2的数是___ .
2和-2,也可合起来写 +2
2.在数轴上表示下列各数,并求它们的绝对值:
, 6 , -3 ,
3.比较下列各组数的大小:
(1) (2)
(3) (4)
4.下面的说法是否正确?请将错误的改正过来.
(1)有理数的绝对值一定比0大;
(2)有理数的相反数一定比0小;
(3)如果两个数的绝对值相等,那么这两个数相等;
(4)互为相反数的两个数的绝对值相等.
(5)字母a表示一个有理数那么-a是负数。
可以等于0
可以是正数,0和负数
还有可能是互为相反数
-a可以是正数,0和负数
1.相反数:如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数。
0的相反数是0
a的相反数是-a
2.绝对值:在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.
一个数 的绝对值记作:│ │
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0 的绝对值是 0.
互为相反数的两个数的绝对值相等.
任何一个有理数的绝对值都是 .
非负数
3.会用绝对值比较两个负数的大小:
两个负数比较大小,绝对值大的反而小.
当堂检测
1. │-5│= , │+3│= ,│0│= .
2.一个数的绝对值是它本身,那么这个数一定是
__________________。
3.用“>、<、=”号填空
│+8│ │-8│ , -5 -8. -4____8
4.如果一个数的绝对值等于 4,那么这个数等于__________.
5.绝对值小于3的整数有___个,分别是 ______________.
1、 某日上午,出租车司机小李在南北走向的商业大道上运营,如果规定向北为正,向南为负,出租车的行车里程如下(单位:km):
-17,-4,+13,-10,-12,+3,-13,+15,+20.
若每千米耗油0.2升,则这天上午该出租车共耗油多少升?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
