人教A版高中数学必修一 2.2.2对数函数及其性质教案(二)教案
文档属性
| 名称 | 人教A版高中数学必修一 2.2.2对数函数及其性质教案(二)教案 |  | |
| 格式 | zip | ||
| 文件大小 | 111.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-18 17:56:33 | ||
图片预览

文档简介
对数函数及其性质
一、教材与学情分析:
本节课为人教版(A版)普通高中课程标准实验教科书(必修1)第二章对数函数及其性质的第二课时,其主要包括三个内容,①同底数的两个对数比较大小(例8) ②对数函数的实际应用(例9).③反函数.例8中3个小题都是同底的对数函数比较大小,相互联系,逐个深入,利用对数函数单调性求解。对数函数的实际应用题部分,主要是让学生体会到对数在实际生活中有广泛的应用,培养学生数学应用意识,提高学生应用数学知识解决实际问题的能力.两个内容实际上统一在函数图象和性质的运用上,使得两个内容不是孤立的知识点,而是服务于对数函数的学习.对于反函数课标要求了解指数函数和对数函数是互为反函数,教学中我们将在反函数的教学中对两种函数图象和性质做一个简单梳理,通过学习进一步明确指、对数函数的关系,培养学生联系的观点,在揭示两种函数的关系中,加深对两种函数的认识.
反函数实际上是指、对数函数关系的整体呈现,具体的体现在函数性质的许多方面,教学中通过几何画板课件,直观展示这种数学关系下,函数性质的变化,有利于发展学生数形结合的思想.使学生感受到数与形的统一,内容与形式的和谐.
本节应用题教学中,通过对教材中例题和练习题的改编,使题目在实际生活的背景中体现更丰富的数学原理,更能引导学生综合运用对数函数的知识,解决问题,既激发了学生学数学、用数学的兴趣,也在解题训练上提升了一个台阶.
二、教学目标:
1.知识与技能
①进一步理解对数函数的图象和性质。
②能应用对数函数性质解决实际中的问题.
③了解反函数的概念,理解同底数的指数函数与对数函数互为反函数.在反函数的研究中加深对指数函数和对数函数性质的理解.
2.过程与方法
①在对数函数图象和性质的教学中,进一步领悟函数思想、等价转化、分类讨论、数形结合的思想.
②在反函数的研究过程中,学生通过观察和类比函数图象,体会两种函数性质上的联系.
③培养学生对应用数学知识解决实际问题的能力,在解题中把具体的实际问题化归为数学问题.
3.情感、态度、价值观
①培养学生严谨的科学态度. 启发学生用所获得的结果去解释实际现象.
②用联系的观点分析问题,认识事物之间的相互转化.
三、重点、难点:
重点:对数函数性质的深化及其应用.
难点:1.对反函数概念的理解,并从中理解指、对数函数图象和性质的关系.
2.如何把具体的实际问题化归为数学问题,利用对数函数模型进行求解.
四、教法:启发引导,探索发现(多媒体辅助教学).
五、学法与教具:
学法:通过图象,理解对数函数与指数函数的关系. 强调要有数形结合、分类讨论、转化的数学思想
教具:多媒体、几何画板
六、教学过程:
(一).复习铺垫导入新课
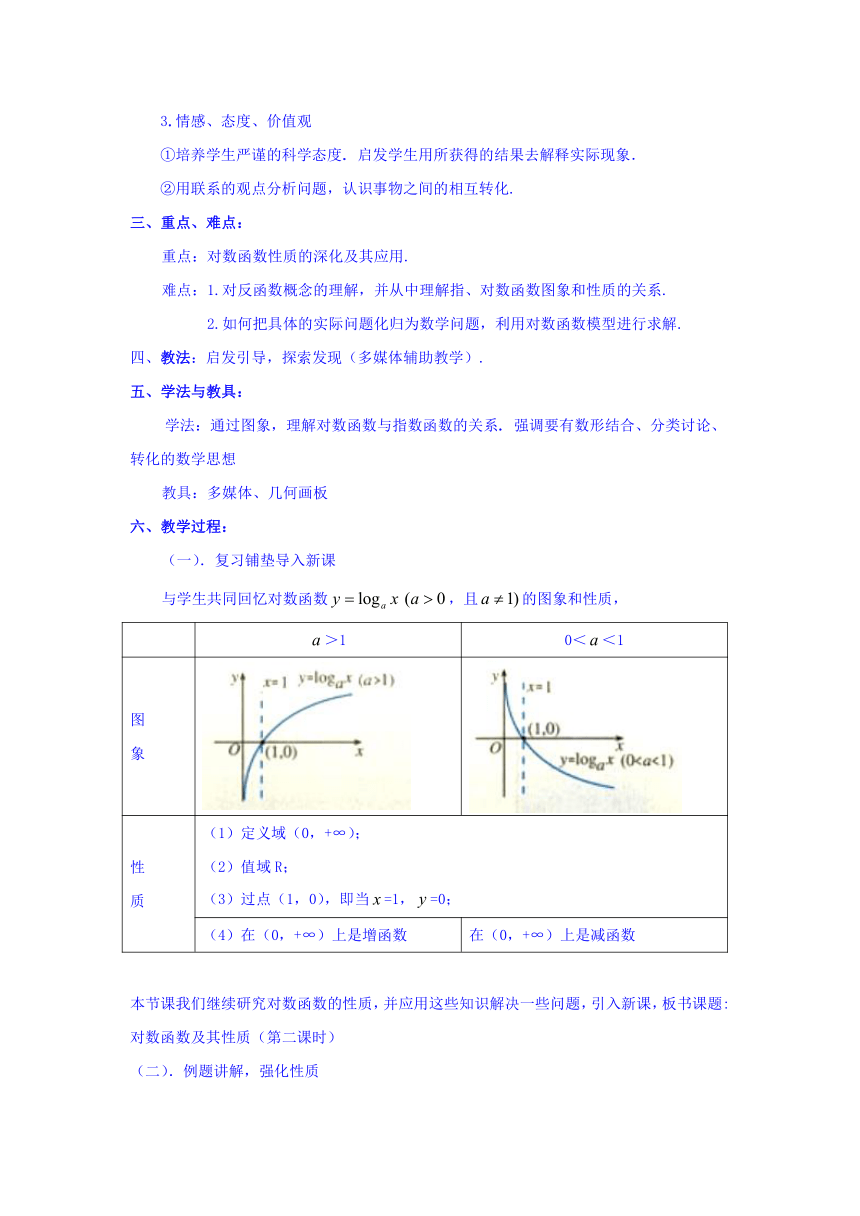
与学生共同回忆对数函数,且的图象和性质,
>1
0<<1
图
象
性
质
(1)定义域(0,+∞);
(2)值域R;
(3)过点(1,0),即当=1,=0;
(4)在(0,+∞)上是增函数
在(0,+∞)上是减函数
本节课我们继续研究对数函数的性质,并应用这些知识解决一些问题,引入新课,板书课题: 对数函数及其性质(第二课时)
(二).例题讲解,强化性质
教师课件展示两个例题
例8 比较下列各组数中两个值的大小:
(1) , (2) ,
(3),
与学生共同完成,教师板书,强化分类讨论的数学思想。
设计意图:例8以渐进式的方式呈现三个题目,(1)(2)注意构造函数应用单调性,(3)在学生认知冲突之后,用分类讨论的思想解题。
例9 溶液的酸碱度是通过pH值来刻画的,pH值的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是mol/L.
(1)已知纯净水中氢离子的浓度为[H+]=10-7mol/L,计算纯净水的pH值.
(2)根据联合国卫生组织的标准,当人体的血液PH值接近7.45的时候,我们可以称之为偏碱性体质,这种体制是最健康的.而中国广西巴马的水不仅矿物质非常丰富,水质PH值为7.5成弱碱性.和人体血液的PH值7.5基本吻合.求巴马水中氢离子的浓度. ()
(3)根据对数函数性质及上述pH值的计算公式,说明溶液的酸碱度与溶液中氢离子的浓度之间的变化关系.
设计意图:例9主要考察学生对实际问题题意的理解,把具体的实际问题化归为数学问题.把课本(2)改为(1),增加(2),对比两组数据,体会溶液的酸碱度与溶液中氢离子的浓度之间的变化关系.可以从的单调性去说明,启发学生用所获得的结果去解释实际现象.本题要求学生独立将实际问题转化为数学问题;在练习本上独立解决.教师指正,之后通过对“对数函数”应用(如航天技术、考古学、生物学等领域)的大致介绍,使学生感受数学的应用价值.强调数学应用思想
(II)学生练习:练习一
1.已知,,,,则( )
A. B. C. D.
2.比较大小:
(1) ;
(2) .(写出推理过程)
3.声强级L(单位:dB)由公式: 给出,其中I为声强(单位:W/m2 ).
(1)平时常人交谈时的声强约为10-6W/m2,求其声强级.
(2)一般正常人听觉能忍受的最高声强为1W/m2 ,能听到的最低声强为10-12W/m2.求人听觉的声强级范围.
设计意图:前两题均是利用了对数函数的图象和性质,但题目编制中注意引导学生转化成例8的问题模型来解决,在强化函数性质同时,培养学生转化与化归的数学思想.第3题本题主要考察学生对实际问题题意的理解,把具体的实际问题化归为数学问题.(1)直接求函数值,(2)强化对数函数单调性应用,培养学生转化的数学思想.培养学生严谨的学习习惯.
(三).深入研究,拓展延伸
(I)教师屏幕展示指数函数和对数函数的简单性质,
指数函数
对数函数
定义域
值域
定点
并组织学生讨论:指、对数函数有何关系:性质中的值是互换的。
教师通过具体的函数引导学生从解析中认识反函数的意义,
(II)以反函数提出的问题为载体,具体研究两种函数性质的一些统一性。
既然指、对数函数中的的值是互换的。那么他又是如何将这样的特点反映在函数的性质上呢?结合图象以性质中值的关系猜想对数函数的相关性质,并作进一步的归纳:
学生猜想
几何画板演示,直观感知操作确认,并把问题推广到一般,归纳性质:同正异负
教学中关注数形结合的思想,尤其是数形结合具体体现形式,培养学生主动应用数形结合思想解决问题的能力。
(四)课堂练习二
1.判断下列数值的正负:
0; 0; 0.
2. 设,则( )
A a研究与探讨(课下完成)
3.比较大小: ; .
(五)小结所学,形成系统:带领学生从知识与方法两个方面进行回顾与总结,
指出:在知识方面,本节知道同底的指数函数和对数函数是互为反函数,又通过反函数类比研究了对数函数的一些性质。在数学思想方法上体会到分类讨论、数形结合、转化与化归在数学解题中的应用,也应用知识解决相关问题的过程中,认识到了对数函数在实际生活中有广泛的应用.实际上对数函数还广泛应用于航天技术、考古学、生物学等领域.
(六)作业:
,
阅读P76探究与发现 “互为反函数的两个函数图象之间的关系”
一、教材与学情分析:
本节课为人教版(A版)普通高中课程标准实验教科书(必修1)第二章对数函数及其性质的第二课时,其主要包括三个内容,①同底数的两个对数比较大小(例8) ②对数函数的实际应用(例9).③反函数.例8中3个小题都是同底的对数函数比较大小,相互联系,逐个深入,利用对数函数单调性求解。对数函数的实际应用题部分,主要是让学生体会到对数在实际生活中有广泛的应用,培养学生数学应用意识,提高学生应用数学知识解决实际问题的能力.两个内容实际上统一在函数图象和性质的运用上,使得两个内容不是孤立的知识点,而是服务于对数函数的学习.对于反函数课标要求了解指数函数和对数函数是互为反函数,教学中我们将在反函数的教学中对两种函数图象和性质做一个简单梳理,通过学习进一步明确指、对数函数的关系,培养学生联系的观点,在揭示两种函数的关系中,加深对两种函数的认识.
反函数实际上是指、对数函数关系的整体呈现,具体的体现在函数性质的许多方面,教学中通过几何画板课件,直观展示这种数学关系下,函数性质的变化,有利于发展学生数形结合的思想.使学生感受到数与形的统一,内容与形式的和谐.
本节应用题教学中,通过对教材中例题和练习题的改编,使题目在实际生活的背景中体现更丰富的数学原理,更能引导学生综合运用对数函数的知识,解决问题,既激发了学生学数学、用数学的兴趣,也在解题训练上提升了一个台阶.
二、教学目标:
1.知识与技能
①进一步理解对数函数的图象和性质。
②能应用对数函数性质解决实际中的问题.
③了解反函数的概念,理解同底数的指数函数与对数函数互为反函数.在反函数的研究中加深对指数函数和对数函数性质的理解.
2.过程与方法
①在对数函数图象和性质的教学中,进一步领悟函数思想、等价转化、分类讨论、数形结合的思想.
②在反函数的研究过程中,学生通过观察和类比函数图象,体会两种函数性质上的联系.
③培养学生对应用数学知识解决实际问题的能力,在解题中把具体的实际问题化归为数学问题.
3.情感、态度、价值观
①培养学生严谨的科学态度. 启发学生用所获得的结果去解释实际现象.
②用联系的观点分析问题,认识事物之间的相互转化.
三、重点、难点:
重点:对数函数性质的深化及其应用.
难点:1.对反函数概念的理解,并从中理解指、对数函数图象和性质的关系.
2.如何把具体的实际问题化归为数学问题,利用对数函数模型进行求解.
四、教法:启发引导,探索发现(多媒体辅助教学).
五、学法与教具:
学法:通过图象,理解对数函数与指数函数的关系. 强调要有数形结合、分类讨论、转化的数学思想
教具:多媒体、几何画板
六、教学过程:
(一).复习铺垫导入新课
与学生共同回忆对数函数,且的图象和性质,
>1
0<<1
图
象
性
质
(1)定义域(0,+∞);
(2)值域R;
(3)过点(1,0),即当=1,=0;
(4)在(0,+∞)上是增函数
在(0,+∞)上是减函数
本节课我们继续研究对数函数的性质,并应用这些知识解决一些问题,引入新课,板书课题: 对数函数及其性质(第二课时)
(二).例题讲解,强化性质
教师课件展示两个例题
例8 比较下列各组数中两个值的大小:
(1) , (2) ,
(3),
与学生共同完成,教师板书,强化分类讨论的数学思想。
设计意图:例8以渐进式的方式呈现三个题目,(1)(2)注意构造函数应用单调性,(3)在学生认知冲突之后,用分类讨论的思想解题。
例9 溶液的酸碱度是通过pH值来刻画的,pH值的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是mol/L.
(1)已知纯净水中氢离子的浓度为[H+]=10-7mol/L,计算纯净水的pH值.
(2)根据联合国卫生组织的标准,当人体的血液PH值接近7.45的时候,我们可以称之为偏碱性体质,这种体制是最健康的.而中国广西巴马的水不仅矿物质非常丰富,水质PH值为7.5成弱碱性.和人体血液的PH值7.5基本吻合.求巴马水中氢离子的浓度. ()
(3)根据对数函数性质及上述pH值的计算公式,说明溶液的酸碱度与溶液中氢离子的浓度之间的变化关系.
设计意图:例9主要考察学生对实际问题题意的理解,把具体的实际问题化归为数学问题.把课本(2)改为(1),增加(2),对比两组数据,体会溶液的酸碱度与溶液中氢离子的浓度之间的变化关系.可以从的单调性去说明,启发学生用所获得的结果去解释实际现象.本题要求学生独立将实际问题转化为数学问题;在练习本上独立解决.教师指正,之后通过对“对数函数”应用(如航天技术、考古学、生物学等领域)的大致介绍,使学生感受数学的应用价值.强调数学应用思想
(II)学生练习:练习一
1.已知,,,,则( )
A. B. C. D.
2.比较大小:
(1) ;
(2) .(写出推理过程)
3.声强级L(单位:dB)由公式: 给出,其中I为声强(单位:W/m2 ).
(1)平时常人交谈时的声强约为10-6W/m2,求其声强级.
(2)一般正常人听觉能忍受的最高声强为1W/m2 ,能听到的最低声强为10-12W/m2.求人听觉的声强级范围.
设计意图:前两题均是利用了对数函数的图象和性质,但题目编制中注意引导学生转化成例8的问题模型来解决,在强化函数性质同时,培养学生转化与化归的数学思想.第3题本题主要考察学生对实际问题题意的理解,把具体的实际问题化归为数学问题.(1)直接求函数值,(2)强化对数函数单调性应用,培养学生转化的数学思想.培养学生严谨的学习习惯.
(三).深入研究,拓展延伸
(I)教师屏幕展示指数函数和对数函数的简单性质,
指数函数
对数函数
定义域
值域
定点
并组织学生讨论:指、对数函数有何关系:性质中的值是互换的。
教师通过具体的函数引导学生从解析中认识反函数的意义,
(II)以反函数提出的问题为载体,具体研究两种函数性质的一些统一性。
既然指、对数函数中的的值是互换的。那么他又是如何将这样的特点反映在函数的性质上呢?结合图象以性质中值的关系猜想对数函数的相关性质,并作进一步的归纳:
学生猜想
几何画板演示,直观感知操作确认,并把问题推广到一般,归纳性质:同正异负
教学中关注数形结合的思想,尤其是数形结合具体体现形式,培养学生主动应用数形结合思想解决问题的能力。
(四)课堂练习二
1.判断下列数值的正负:
0; 0; 0.
2. 设,则( )
A a
3.比较大小: ; .
(五)小结所学,形成系统:带领学生从知识与方法两个方面进行回顾与总结,
指出:在知识方面,本节知道同底的指数函数和对数函数是互为反函数,又通过反函数类比研究了对数函数的一些性质。在数学思想方法上体会到分类讨论、数形结合、转化与化归在数学解题中的应用,也应用知识解决相关问题的过程中,认识到了对数函数在实际生活中有广泛的应用.实际上对数函数还广泛应用于航天技术、考古学、生物学等领域.
(六)作业:
,
阅读P76探究与发现 “互为反函数的两个函数图象之间的关系”
