2.3幂函数 27张
图片预览







文档简介
(共29张PPT)
§2.3幂函数
高中数学必修 ①人教版A
一、复习引入
1、求函数y=x1/2的定义域
2、判断函数y=x3的奇偶性
二、自学
思考1:如果张红购买了每千克1元的水果x千克,她需要付的钱数为y(元),试将y表示成x的函数.
思考2:如果正方形的边长为x,面积为y,试将y表示成x的函数.
思考3:如果正方体的边长为x,体积为y,试将y表示成x的函数.
思考4:如果一个正方形场地的面积为x,正方形的边长为y,试将y表示成x的函数.
思考5:如果某人x秒内骑车行进了1km,他骑车的平均速度为y,试将y表示成x的函数.
思考6:以上是我们生活中遇到的几个函数问题,这些函数是指数函数吗?你能发现这几个函数的解析式有什么共同特点吗?
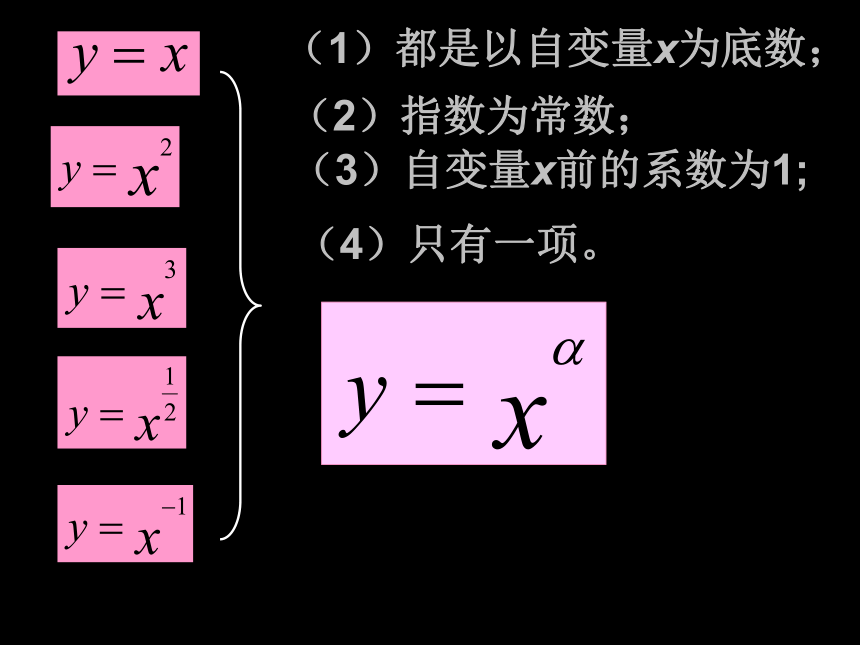
(1)都是以自变量x为底数;
(2)指数为常数;
(3)自变量x前的系数为1;
(4)只有一项。
一、定义
几点说明:
例1:
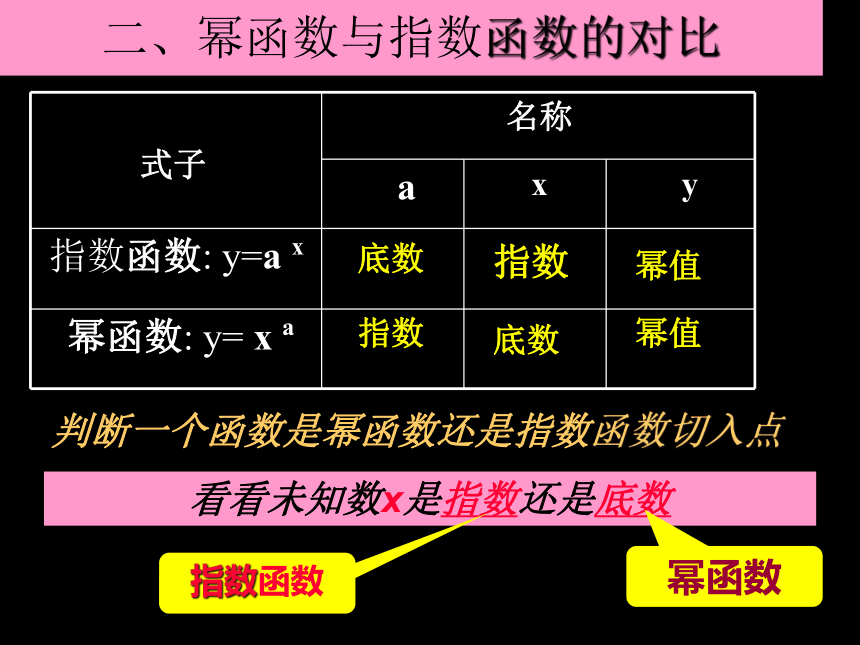
二、幂函数与指数函数的对比
底数
指数
指数
底数
幂值
幂值
判断一个函数是幂函数还是指数函数切入点
看看未知数x是指数还是底数
幂函数
指数函数
式子 名称
a x y
指数函数: y=a x
幂函数: y= x a
(指数函数)
(幂函数)
(指数函数)
(幂函数)
快速反应
(指数函数)
(幂函数)
三、五个常用幂函数的图像和性质
定义域:
值 域:
奇偶性:
单调性:
定义域:
值 域:
奇偶性:
单调性:
定义域:
值 域:
奇偶性:
单调性:
-8
-1
0
1
8
27
0
1
0
x
y
y=x3
/
/
64
2
x … -2 -1 0 1 2 3 4 …
y=x3 … …
y=x1/2 … …
定义域:
值 域:
奇偶性:
单调性:
定义域:
值 域:
奇偶性:
单调性:
函数 的图像
幂函数的定义域、值域、奇偶性和单调性,随常数α取值的不同而不同.
y = x
R
R
R
[0,+∞)
R
[0,+∞)
R
[0,+∞)
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
在R上是增函数
在(-∞,0]上是减函数,在(0, +∞)上是增函数
在R上是增函数
在(0,+∞)上是增函数
在( -∞,0),(0, +∞)上是减函数
(1,1)
奇偶性
y = x2
y= x3
定义域
值 域
单调性
公共点
下面将5个函数的图像画在同一坐标系中
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
y=x
在第一象限内,
a >0,在(0,+∞)上为增函数;
a <0,在(0,+∞)上为减函数.
幂函数的图象都通过点(1,1)
α为奇数时,幂函数为奇函数,
α为偶数时,幂函数为偶函数.
方法技巧:分子有理化
解:(1)y= x0.8在(0,∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8
(2)y=x0.3在(0,∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3
(3)y=x-2/5在(0,∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5
练习(4)
2)
4)
<
<
>
>
知识理解、运用
a=1
小结: 幂函数的性质:
1.所有幂函数的图象都通过点(1,1);
幂函数的定义域、值域、奇偶性和单调性,随常数α取值的不同而不同.
如果α<0,则幂函数
在(0,+∞)上为减函数。
3.如果α>0,则幂函数
在(0,+∞)上为增函数;
2.当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数.
作业:
利用单调性判断下列各值的大小。
§2.3幂函数
高中数学必修 ①人教版A
一、复习引入
1、求函数y=x1/2的定义域
2、判断函数y=x3的奇偶性
二、自学
思考1:如果张红购买了每千克1元的水果x千克,她需要付的钱数为y(元),试将y表示成x的函数.
思考2:如果正方形的边长为x,面积为y,试将y表示成x的函数.
思考3:如果正方体的边长为x,体积为y,试将y表示成x的函数.
思考4:如果一个正方形场地的面积为x,正方形的边长为y,试将y表示成x的函数.
思考5:如果某人x秒内骑车行进了1km,他骑车的平均速度为y,试将y表示成x的函数.
思考6:以上是我们生活中遇到的几个函数问题,这些函数是指数函数吗?你能发现这几个函数的解析式有什么共同特点吗?
(1)都是以自变量x为底数;
(2)指数为常数;
(3)自变量x前的系数为1;
(4)只有一项。
一、定义
几点说明:
例1:
二、幂函数与指数函数的对比
底数
指数
指数
底数
幂值
幂值
判断一个函数是幂函数还是指数函数切入点
看看未知数x是指数还是底数
幂函数
指数函数
式子 名称
a x y
指数函数: y=a x
幂函数: y= x a
(指数函数)
(幂函数)
(指数函数)
(幂函数)
快速反应
(指数函数)
(幂函数)
三、五个常用幂函数的图像和性质
定义域:
值 域:
奇偶性:
单调性:
定义域:
值 域:
奇偶性:
单调性:
定义域:
值 域:
奇偶性:
单调性:
-8
-1
0
1
8
27
0
1
0
x
y
y=x3
/
/
64
2
x … -2 -1 0 1 2 3 4 …
y=x3 … …
y=x1/2 … …
定义域:
值 域:
奇偶性:
单调性:
定义域:
值 域:
奇偶性:
单调性:
函数 的图像
幂函数的定义域、值域、奇偶性和单调性,随常数α取值的不同而不同.
y = x
R
R
R
[0,+∞)
R
[0,+∞)
R
[0,+∞)
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
在R上是增函数
在(-∞,0]上是减函数,在(0, +∞)上是增函数
在R上是增函数
在(0,+∞)上是增函数
在( -∞,0),(0, +∞)上是减函数
(1,1)
奇偶性
y = x2
y= x3
定义域
值 域
单调性
公共点
下面将5个函数的图像画在同一坐标系中
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
y=x
在第一象限内,
a >0,在(0,+∞)上为增函数;
a <0,在(0,+∞)上为减函数.
幂函数的图象都通过点(1,1)
α为奇数时,幂函数为奇函数,
α为偶数时,幂函数为偶函数.
方法技巧:分子有理化
解:(1)y= x0.8在(0,∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8
(2)y=x0.3在(0,∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3
(3)y=x-2/5在(0,∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5
练习(4)
2)
4)
<
<
>
>
知识理解、运用
a=1
小结: 幂函数的性质:
1.所有幂函数的图象都通过点(1,1);
幂函数的定义域、值域、奇偶性和单调性,随常数α取值的不同而不同.
如果α<0,则幂函数
在(0,+∞)上为减函数。
3.如果α>0,则幂函数
在(0,+∞)上为增函数;
2.当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数.
作业:
利用单调性判断下列各值的大小。
