必修1 第二章 基本初等函数小结 19张
文档属性
| 名称 | 必修1 第二章 基本初等函数小结 19张 |

|
|
| 格式 | zip | ||
| 文件大小 | 790.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-18 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
基本初等函数本章小结
代 兵
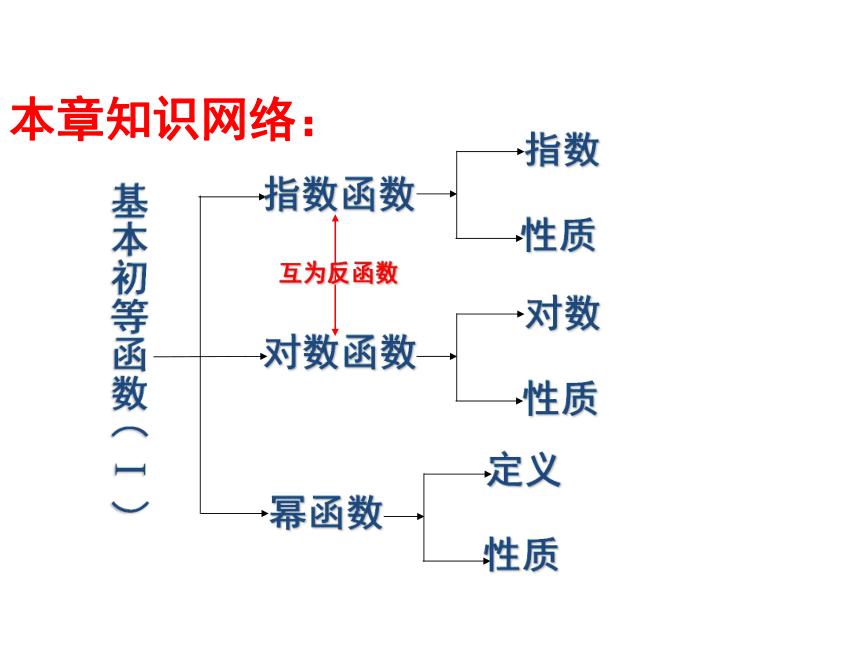
本章知识网络:
高中数学必修1同步辅导课程——基本初等函数本章小结
基本初等函数(Ⅰ)
指数函数
幂函数
对数函数
指数
性质
对数
性质
定义
性质
互为反函数
指数函数与对数函数的联系:
高中数学必修1同步辅导课程——基本初等函数本章小结
图像:
例1:(1)化简:
高中数学必修1同步辅导课程——基本初等函数本章小结
典型题例:
(2)求值:
变式:(1)已知:
的值。
高中数学必修1同步辅导课程——基本初等函数本章小结
的值。
(2)已知:
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
例3:
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
变式2:
设函数
上不是单调函数的条件是( )
O
y
x
1
,则
在区间(m,2m+1)(m>0)
高中数学必修1同步辅导课程——基本初等函数本章小结
变式2:已知函数f(x)=ln[(5+k)x2+6x+k+5]
(1)若f(x)的定义域为R,求实数k的取值范围;
高中数学必修1同步辅导课程——基本初等函数本章小结
变式2:已知函数f(x)=ln[(5+k)x2+6x+k+5]
(2)若f(x)的值域为R,求实数k的取值范围;
高中数学必修1同步辅导课程——基本初等函数本章小结
(1)定义域为R,意味着真数恒大于零.
对于不等式(5+k)x2+6x+k+5>0不能简单认为是二次不等式.注意分类讨论(二次项系数含有参数).
(2)设y=logau(x)(0真数u(x)就必须取遍(0,+∞)内的所有值,u(x)在作为真数之前,是否出现负值或零无关紧要,关键是u(x)的取值要包含(0,+∞)中的所有值.
至于u(x)中的负值及零只要通过定义域要求去掉即可.
解题回顾:
变式2:已知函数f(x)=ln[(5+k)x2+6x+k+5]
(1)若f(x)的定义域为R,求实数k的取值范围;
(2)若f(x)的值域为R,求实数k的取值范围;
高中数学必修1同步辅导课程——基本初等函数本章小结
课堂总结:
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
指数函数
指数
性质
根式:a的n次方根
分数指数幂:
运算性质:
解析式:
图像:
定义域:R
单调性:a>1时为增函数,0定点:(0,1)
值域:( );
高中数学必修1同步辅导课程——基本初等函数本章小结
对数函数
对数
性质
运算性质:
解析式:
图像:
定义域:( )
定点:(1,0)
值域:R
定义: ,x叫做以a为底N的对数
换底公式:
单调性:a>1时为增函数,0高中数学必修1同步辅导课程——基本初等函数本章小结
幂函数
定义:形如 (a是常数)
五个具体
的幂函数
(a=-1, ,0,1,2)
如果a>0,则图象过点(0,0)、(1,1)并在(0,+∞)上为增函数;
如果a<0,则图象过点(1,1),
并在(0,+∞)上为减函数;
基本初等函数本章小结
代 兵
本章知识网络:
高中数学必修1同步辅导课程——基本初等函数本章小结
基本初等函数(Ⅰ)
指数函数
幂函数
对数函数
指数
性质
对数
性质
定义
性质
互为反函数
指数函数与对数函数的联系:
高中数学必修1同步辅导课程——基本初等函数本章小结
图像:
例1:(1)化简:
高中数学必修1同步辅导课程——基本初等函数本章小结
典型题例:
(2)求值:
变式:(1)已知:
的值。
高中数学必修1同步辅导课程——基本初等函数本章小结
的值。
(2)已知:
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
例3:
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
变式2:
设函数
上不是单调函数的条件是( )
O
y
x
1
,则
在区间(m,2m+1)(m>0)
高中数学必修1同步辅导课程——基本初等函数本章小结
变式2:已知函数f(x)=ln[(5+k)x2+6x+k+5]
(1)若f(x)的定义域为R,求实数k的取值范围;
高中数学必修1同步辅导课程——基本初等函数本章小结
变式2:已知函数f(x)=ln[(5+k)x2+6x+k+5]
(2)若f(x)的值域为R,求实数k的取值范围;
高中数学必修1同步辅导课程——基本初等函数本章小结
(1)定义域为R,意味着真数恒大于零.
对于不等式(5+k)x2+6x+k+5>0不能简单认为是二次不等式.注意分类讨论(二次项系数含有参数).
(2)设y=logau(x)(0
至于u(x)中的负值及零只要通过定义域要求去掉即可.
解题回顾:
变式2:已知函数f(x)=ln[(5+k)x2+6x+k+5]
(1)若f(x)的定义域为R,求实数k的取值范围;
(2)若f(x)的值域为R,求实数k的取值范围;
高中数学必修1同步辅导课程——基本初等函数本章小结
课堂总结:
高中数学必修1同步辅导课程——基本初等函数本章小结
高中数学必修1同步辅导课程——基本初等函数本章小结
指数函数
指数
性质
根式:a的n次方根
分数指数幂:
运算性质:
解析式:
图像:
定义域:R
单调性:a>1时为增函数,0
值域:( );
高中数学必修1同步辅导课程——基本初等函数本章小结
对数函数
对数
性质
运算性质:
解析式:
图像:
定义域:( )
定点:(1,0)
值域:R
定义: ,x叫做以a为底N的对数
换底公式:
单调性:a>1时为增函数,0
幂函数
定义:形如 (a是常数)
五个具体
的幂函数
(a=-1, ,0,1,2)
如果a>0,则图象过点(0,0)、(1,1)并在(0,+∞)上为增函数;
如果a<0,则图象过点(1,1),
并在(0,+∞)上为减函数;
