第一章 反比例函数单元测试题(含答案)
图片预览


文档简介
鲁教版数学九年级第一单元测试题(A)
时间:60分钟 满分:100分
一、选择题(30分)
1.(淮安中考)若点A(-2,3)在反比例函数的图象上,则k的值是( )
A. -6 B. -2 C.2 D.6
2.(衡阳中考)对于反比例函数,下列说法不正确的是( )
A.图象分布在第二、四象限 B.当x>0时,y随x的增大而增大
C.图象经过点(1,-2) D.若点A(x1,y1),B(x2,y2)都在图象上,且x13.(徐州中考)如果点(3,-4)在反比例函数的图象上,那么下列各点中,在此图象上的是( )
A.(3,4) B.(-2,-6) C.(-2,6) D.(-3,-4)
4.已知反比例函数,当1A.010
5.(扬州中考)已知点A(x1,3),B(x2,6)都在反比例函数的图象上,则下列关系式一定正确的是( )
A.x16.一司机驾驶汽车从甲地去乙地,他以80千米/小时的平均速度用了4小时到达乙地,当他按原路匀速返回时,汽车的速度v(千米/小时)与时间t(小时)之间的函数关系式是( )
A.v=320t B. C.v=20t D.
7.如图,直线与x轴交于点A,与双曲线交于点B,若S△AOB=2,则b的值是( )
A.4 B.3 C.2 D.1
8.(大庆中考)在同一直角坐标系中,函数和的图象大致是( )
9.(黄石中考)已知一次函数y1=x-3和反比例函数y2=的图象在平面直角坐标系中交于A、B两点,当y1>y2时,x的取值范围是( )
A.x<-1或x>4 B.-1<x<0或x>4 C.-1<x<0或0<x<4 D.x<-1或0<x<4
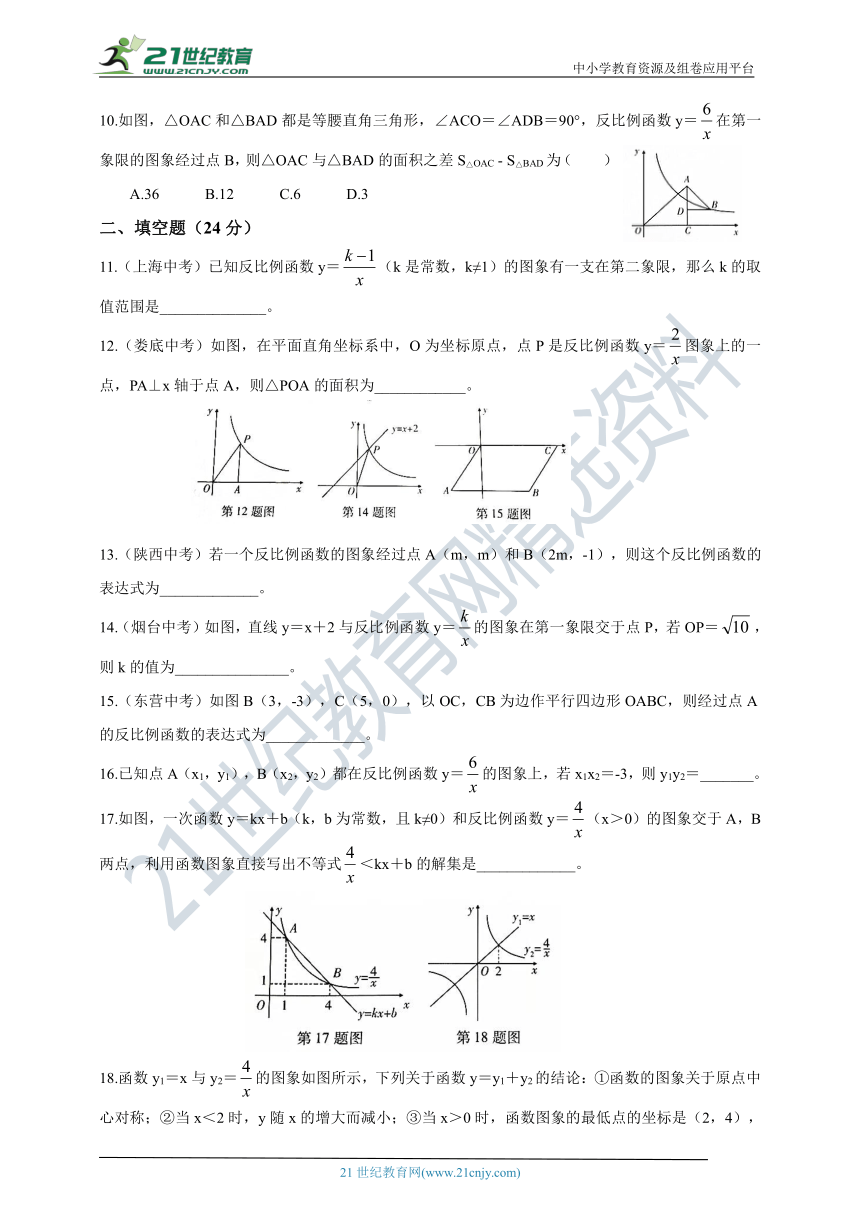
10.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC - S△BAD为( )
A.36 B.12 C.6 D.3
二、填空题(24分)
11.(上海中考)已知反比例函数y=(k是常数,k≠1)的图象有一支在第二象限,那么k的取值范围是______________。
12.(娄底中考)如图,在平面直角坐标系中,O为坐标原点,点P是反比例函数y=图象上的一点,PA⊥x轴于点A,则△POA的面积为____________。
13.(陕西中考)若一个反比例函数的图象经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为_____________。
14.(烟台中考)如图,直线y=x+2与反比例函数y=的图象在第一象限交于点P,若OP=,则k的值为_______________。
15.(东营中考)如图B(3,-3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的表达式为_____________。
16.已知点A(x1,y1),B(x2,y2)都在反比例函数y=的图象上,若x1x2=-3,则y1y2=_______。
17.如图,一次函数y=kx+b(k,b为常数,且k≠0)和反比例函数y=(x>0)的图象交于A,B两点,利用函数图象直接写出不等式<kx+b的解集是_____________。
18.函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数图象的最低点的坐标是(2,4),其中所有正确结论的序号是______________。
三、解答题(6+8+10+10+12=36分)
19.如图,已知反比例函数y=图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2。
(1)求k和m的值。
(2)若点C(x,y)也在反比例函数y=的图象上,当-3≤x≤-1时,求函数y的取值范围。
20.(杭州中考)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货。设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)。
(1)求v关于t的函数表达式。
(2)若要求不超过5小时卸完船上的这批货物,则平均每小时至少要卸货多少吨?
21.(潍坊中考)如图,直线y=3x - 5与反比例函数y=的图象相交于A(2,m),B(n,- 6)两点,连接OA,OB。
(1)求k和n的值。
(2)求△AOB的面积。
22.(菏泽中考)如图,已知点D在反比例函数y=的图象上,过点D作DB⊥y轴,垂足为B(0,3),直线y=kx+b经过点A(5,0),与y轴交于点C且BD=OC,OC:OA=2:5。
(1)求反比例函数y=和一次函数y=kx+b的表达式。
(2)直接写出关于x的不等式>kx+b的解集。
23.如图,直线y=2x+3与y轴交于点A,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0)。
(1)求反比例函数的表达式。
(2)点D(a,1)是反比例函数y=(x>0)象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由。
参考答案
一、1.A 2.D 3.C 4.C 5.A 6.B 7.D 8.B 9.B 10.D
二、11.k<1 12.1 13. y= 14. 3 15.y=
- 12 17. 1< x < 4 18.①③
三、19.解(1)△AOB的面积为2,∴k=4,∴反比例函数的表达式为。∵反比例函数的图象经过点A(4,m),∴。
(2)∵当x=-3时,;当x=-1时,y=-4,又∵反比例函数在x<0时,y随x的增大而减小,∴当-3≤x≤-1时,y的取值范围为-4≤y≤。
20.解:(1)由题意可得vt=100,则v=(t>0).
(2)∵要求不超过5小时卸完船上的这批货物,∴0<t≤5,则v≥=20,即平均每小时至少要卸货20吨。
21.解:(1)∵点B(n,- 6)在直线y=3x - 5上,∴ - 6=3n - 5,解得n=,∴B(,- 6)。∵反比例函数y=的图象连点B,∴k - 1=-×(-6)=2,∴k=3.
(2)设直线y=3x - 5分别与x轴、y轴交于C,D两点。当y=0时,3x-5=0,x=,即OC=。当x=0时,y=3×0 - 5= - 5,即OD=5。∴A(2,m)在直线y=3x - 5上,∴m=3×2 - 5=1,即A(2,1),∴S△AOB=S△BOD+S△COD+S△AOC=。
22.解:(1)BD=OC,OC:OA=2:5,点A(5,0),点B(0,3),∴OA=5,OC=BD=2,OB=3。又∵点C在y轴负轴,点D在第二象限,∴点C的坐标为(0,-2),点D的坐标为(-2,3)。∵点D(-2,3)在反比例函数y=的图象上,∴a=-2×3= - 6,∴反比例函数的表式为y=。将A(5,0),C(0,-2)代入y=k+b,得,解得,∴一次函数的表达式为。(2)不等式>kx+b的解集为x<0。
23.解:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),∴在直线y=2x+3中,当x=1时,y=2+3=5,∴点B的坐标为(1,5),又∵点B(1,5)在反比例函数y=上,∴k=1×5=5,∴反比例函的表达式为y=。
(2)将点D(a,1)代入y=,得a=5,∴点D标为(5,1)。设点D(5,1)关于x轴的对称点为D'(5,-1)。设点B(1,5),点D'(5,-1)的直线表达式为y=kx+b,得,解得,∴直线BD'的表达式为y=。根据题意知,直线BD'与x轴的交点即为所求点P,当y=0时,=0,解得,故点P的坐标为(,0)。
时间:60分钟 满分:100分
一、选择题(30分)
1.(淮安中考)若点A(-2,3)在反比例函数的图象上,则k的值是( )
A. -6 B. -2 C.2 D.6
2.(衡阳中考)对于反比例函数,下列说法不正确的是( )
A.图象分布在第二、四象限 B.当x>0时,y随x的增大而增大
C.图象经过点(1,-2) D.若点A(x1,y1),B(x2,y2)都在图象上,且x1
A.(3,4) B.(-2,-6) C.(-2,6) D.(-3,-4)
4.已知反比例函数,当1
5.(扬州中考)已知点A(x1,3),B(x2,6)都在反比例函数的图象上,则下列关系式一定正确的是( )
A.x1
A.v=320t B. C.v=20t D.
7.如图,直线与x轴交于点A,与双曲线交于点B,若S△AOB=2,则b的值是( )
A.4 B.3 C.2 D.1
8.(大庆中考)在同一直角坐标系中,函数和的图象大致是( )
9.(黄石中考)已知一次函数y1=x-3和反比例函数y2=的图象在平面直角坐标系中交于A、B两点,当y1>y2时,x的取值范围是( )
A.x<-1或x>4 B.-1<x<0或x>4 C.-1<x<0或0<x<4 D.x<-1或0<x<4
10.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC - S△BAD为( )
A.36 B.12 C.6 D.3
二、填空题(24分)
11.(上海中考)已知反比例函数y=(k是常数,k≠1)的图象有一支在第二象限,那么k的取值范围是______________。
12.(娄底中考)如图,在平面直角坐标系中,O为坐标原点,点P是反比例函数y=图象上的一点,PA⊥x轴于点A,则△POA的面积为____________。
13.(陕西中考)若一个反比例函数的图象经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为_____________。
14.(烟台中考)如图,直线y=x+2与反比例函数y=的图象在第一象限交于点P,若OP=,则k的值为_______________。
15.(东营中考)如图B(3,-3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的表达式为_____________。
16.已知点A(x1,y1),B(x2,y2)都在反比例函数y=的图象上,若x1x2=-3,则y1y2=_______。
17.如图,一次函数y=kx+b(k,b为常数,且k≠0)和反比例函数y=(x>0)的图象交于A,B两点,利用函数图象直接写出不等式<kx+b的解集是_____________。
18.函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数图象的最低点的坐标是(2,4),其中所有正确结论的序号是______________。
三、解答题(6+8+10+10+12=36分)
19.如图,已知反比例函数y=图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2。
(1)求k和m的值。
(2)若点C(x,y)也在反比例函数y=的图象上,当-3≤x≤-1时,求函数y的取值范围。
20.(杭州中考)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货。设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)。
(1)求v关于t的函数表达式。
(2)若要求不超过5小时卸完船上的这批货物,则平均每小时至少要卸货多少吨?
21.(潍坊中考)如图,直线y=3x - 5与反比例函数y=的图象相交于A(2,m),B(n,- 6)两点,连接OA,OB。
(1)求k和n的值。
(2)求△AOB的面积。
22.(菏泽中考)如图,已知点D在反比例函数y=的图象上,过点D作DB⊥y轴,垂足为B(0,3),直线y=kx+b经过点A(5,0),与y轴交于点C且BD=OC,OC:OA=2:5。
(1)求反比例函数y=和一次函数y=kx+b的表达式。
(2)直接写出关于x的不等式>kx+b的解集。
23.如图,直线y=2x+3与y轴交于点A,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0)。
(1)求反比例函数的表达式。
(2)点D(a,1)是反比例函数y=(x>0)象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由。
参考答案
一、1.A 2.D 3.C 4.C 5.A 6.B 7.D 8.B 9.B 10.D
二、11.k<1 12.1 13. y= 14. 3 15.y=
- 12 17. 1< x < 4 18.①③
三、19.解(1)△AOB的面积为2,∴k=4,∴反比例函数的表达式为。∵反比例函数的图象经过点A(4,m),∴。
(2)∵当x=-3时,;当x=-1时,y=-4,又∵反比例函数在x<0时,y随x的增大而减小,∴当-3≤x≤-1时,y的取值范围为-4≤y≤。
20.解:(1)由题意可得vt=100,则v=(t>0).
(2)∵要求不超过5小时卸完船上的这批货物,∴0<t≤5,则v≥=20,即平均每小时至少要卸货20吨。
21.解:(1)∵点B(n,- 6)在直线y=3x - 5上,∴ - 6=3n - 5,解得n=,∴B(,- 6)。∵反比例函数y=的图象连点B,∴k - 1=-×(-6)=2,∴k=3.
(2)设直线y=3x - 5分别与x轴、y轴交于C,D两点。当y=0时,3x-5=0,x=,即OC=。当x=0时,y=3×0 - 5= - 5,即OD=5。∴A(2,m)在直线y=3x - 5上,∴m=3×2 - 5=1,即A(2,1),∴S△AOB=S△BOD+S△COD+S△AOC=。
22.解:(1)BD=OC,OC:OA=2:5,点A(5,0),点B(0,3),∴OA=5,OC=BD=2,OB=3。又∵点C在y轴负轴,点D在第二象限,∴点C的坐标为(0,-2),点D的坐标为(-2,3)。∵点D(-2,3)在反比例函数y=的图象上,∴a=-2×3= - 6,∴反比例函数的表式为y=。将A(5,0),C(0,-2)代入y=k+b,得,解得,∴一次函数的表达式为。(2)不等式>kx+b的解集为x<0。
23.解:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),∴在直线y=2x+3中,当x=1时,y=2+3=5,∴点B的坐标为(1,5),又∵点B(1,5)在反比例函数y=上,∴k=1×5=5,∴反比例函的表达式为y=。
(2)将点D(a,1)代入y=,得a=5,∴点D标为(5,1)。设点D(5,1)关于x轴的对称点为D'(5,-1)。设点B(1,5),点D'(5,-1)的直线表达式为y=kx+b,得,解得,∴直线BD'的表达式为y=。根据题意知,直线BD'与x轴的交点即为所求点P,当y=0时,=0,解得,故点P的坐标为(,0)。
