北师大版初中数学七年级上册知识讲解,巩固练习(教学资料,补习资料):第14讲 线段、射线、直线(基础)
文档属性
| 名称 | 北师大版初中数学七年级上册知识讲解,巩固练习(教学资料,补习资料):第14讲 线段、射线、直线(基础) |  | |
| 格式 | zip | ||
| 文件大小 | 266.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-18 11:51:55 | ||
图片预览




文档简介
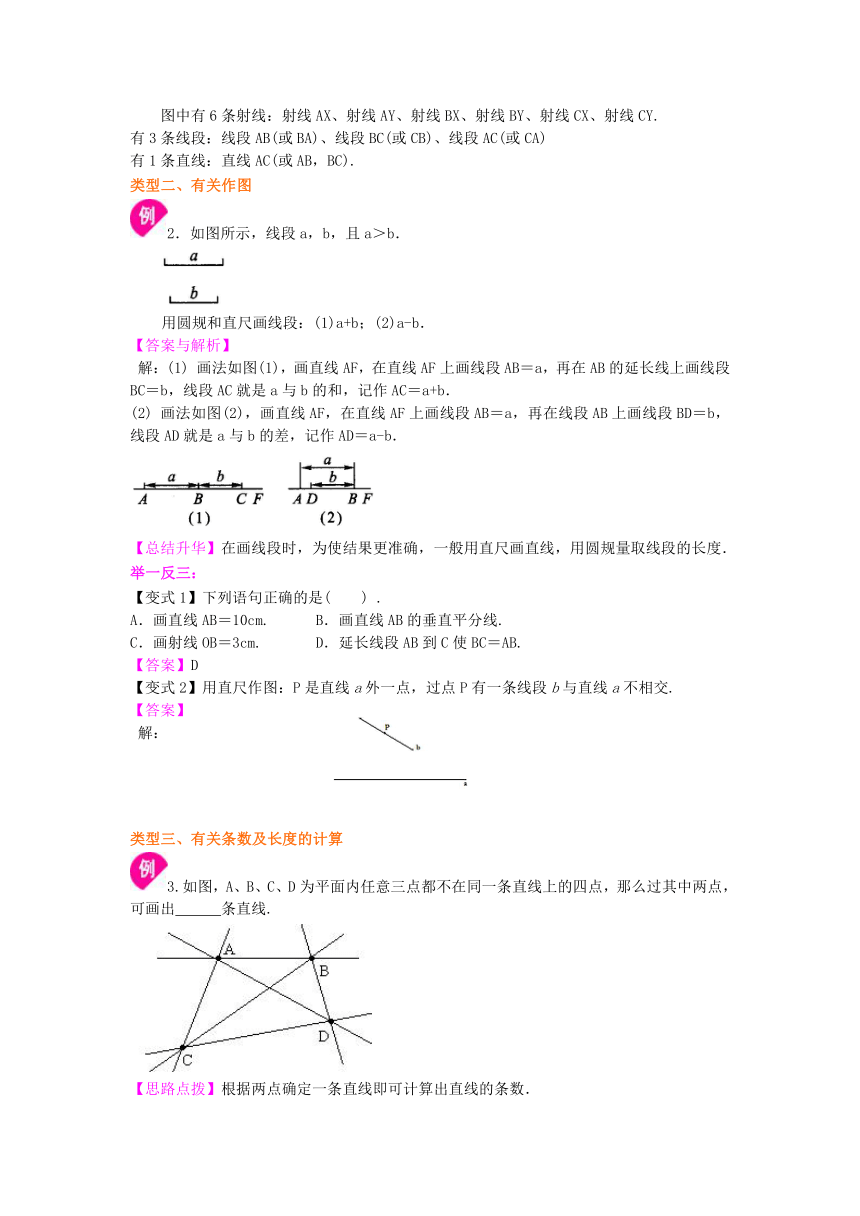
线段、射线、直线(基础)知识讲解
【学习目标】
1.在现实情境中进一步理解线段、射线、直线,并会用不同的方式表示;
2. 通过操作活动,了解“两点确定一条直线”的几何事实,积累数学活动经验;
3. 能够运用几何事实解释和解决具体情境中的实际问题;
4. 通过从事观察、比较、概括等活动,发展抽象思维能力和有条理的数学表达能力.
【要点梳理】
要点一、线段、射线、直线的概念及表示方法
1.概念:绷紧的琴弦、黑板的边沿都可以近似地看作线段,如果把“线段”作为最简单、最基本原始概念,则用“线段”定义射线和直线如下:
(1)将线段向一个方向无限延长就形成了射线.
(2)将线段向两个方向无限延长就形成了直线.
要点诠释:
(1)线段有两个端点,可以度量,可以比较长短.
(2)射线只向一方无限延伸,有一个端点,不能度量,不能比较大小.
(3)直线是向两方无限延伸的,无端点,不可度量,不能比较大小.
(4)线段、射线、直线都没有粗细.
2.表示方法:如图1、图2、图3,线段、射线、直线的表示方法都有两种:它们都可以用两个大写字母表示,也可以一个小写字母表示.
要点诠释:
(1)从表示方法上看,虽然它们都可以用一个小写字母表示,也可以用两个大写字母表示,但直线取得是直线上任意两点的字母,线段用的是两个端点的字母,射线用的是一个端点和任意一点的字母,而直线和线段的两个大写字母没有顺序之分,但射线的两个大写字母有顺序之分,第一个大写字母必须是表示端点.即端点相同,而延伸方向不同,表示不同的射线.如下图4中射线OA,射线OB是不同的射线;
端点相同且延伸方向也相同的射线,表示同一条射线.如下图5中射线OA、射线OB、射线OC都表示同一条射线.
(2)表示直线、射线与线段时,勿忘在字母的前面写上“直线”“射线”“线段”字样.
3.线段、射线、直线的区别与联系
线段
射线
直线
图示
表示方法
线段AB或线段a
射线OA或射线a
直线AB或直线a
端点
两个
一个
无
长度
可度量
不可度量
不可度量
延伸性
不向两方延伸
向一方无限延伸
向两方无限延伸
要点二、基本性质
1. 直线的性质:经过两点有且只有一条直线.简单说成:两点确定一条直线.
要点诠释:
(1)点和直线的位置关系有两种:
①点在直线上,或者说直线经过这个点.如图6中,点O在直线l上,也可以说成是直线l经过点O;
②点在直线外,或者说直线不经过这个点.如图6中,点P在直线l外,也可以说直线l不经过点P.
(2)两条不同的直线相交只有一个交点.
2.线段的基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.
如图7所示,在A,B两点所连的线中,线段AB的长度是最短的.
要点诠释:
(1)连接两点间的线段的长度,叫做这两点的距离.
(2)两条线段可能无公共点,可能有一个公共点,也可能有无穷多个公共点.
要点三、比较线段的长短
1. “作一条线段等于已知线段”的两种方法:
法一:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a.
法二:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a的长度,再画一条等于这个长度的线段.
要点诠释:几何中连结两点,即画出以这两点为端点的线段.
2.线段的比较:
(1)度量法:用刻度尺量出两条线段的长度,再比较长短.
(2)叠合法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:
3.线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如下图,点C是线段AB的中点,则,或AB=2AC=2BC.
要点诠释:若点C是线段AB的中点,则点C一定在线段AB上.
【典型例题】
类型一、相关概念
1.下列说法中,正确的是( ) .
A.射线OA与射线AO是同一条射线.
B.线段AB与线段BA是同一条线段.
C.过一点只能画一条直线.
D.三条直线两两相交,必有三个交点.
【答案】B
【解析】射线OA的端点是O,射线AO的端点是A,所以射线OA与射线AO不是同一条射线,故A错误;过一点能画无数条直线,所以C错误;三条直线两两相交,有三个交点或一个交点(三条直线相交于一点时),所以D错误;线段AB与线段BA是同一条线段,所以B正确.
【总结升华】直线和线段用两个大写字母表示时,与字母的前后顺序无关,但射线必须是表示端点的字母写在前面,不能互换.
举一反三:
【变式1】以下说法中正确的是??( ).
A.延长线段AB到C B.延长射线AB
C.直线AB的端点之一是A D.延长射线OA到C
【答案】A
【变式2】如图所示,请分别指出图中的线段、射线和直线的条数,并把它们分别表示出来.
【答案】
解:如下图所示,在直线上点A左侧和点C右侧分别任取点X和Y.
图中有6条射线:射线AX、射线AY、射线BX、射线BY、射线CX、射线CY.
有3条线段:线段AB(或BA)、线段BC(或CB)、线段AC(或CA)
有1条直线:直线AC(或AB,BC).
类型二、有关作图
2.如图所示,线段a,b,且a>b.
用圆规和直尺画线段:(1)a+b;(2)a-b.
【答案与解析】
解:(1) 画法如图(1),画直线AF,在直线AF上画线段AB=a,再在AB的延长线上画线段BC=b,线段AC就是a与b的和,记作AC=a+b.
(2) 画法如图(2),画直线AF,在直线AF上画线段AB=a,再在线段AB上画线段BD=b,线段AD就是a与b的差,记作AD=a-b.
【总结升华】在画线段时,为使结果更准确,一般用直尺画直线,用圆规量取线段的长度.
举一反三:
【变式1】下列语句正确的是( ) .
A.画直线AB=10cm. B.画直线AB的垂直平分线.
C.画射线OB=3cm. D.延长线段AB到C使BC=AB.
【答案】D
【变式2】用直尺作图:P是直线a外一点,过点P有一条线段b与直线a不相交.
【答案】
解:
类型三、有关条数及长度的计算
3.如图,A、B、C、D为平面内任意三点都不在同一条直线上的四点,那么过其中两点,可画出 条直线.
【思路点拨】根据两点确定一条直线即可计算出直线的条数.
【答案】6条直线
【解析】由两点确定一条直线知,点A与B,C,D三点各确定一条直线,同理点B与C、D各确定一条直线,C与D确定一条直线,综上:共有直线:3+2+1=6(条).
【总结升华】平面上有个点,其中任意三点不在一条直线上,则最多确定的直线条数为:.
举一反三:
【变式1】如图所示,已知线段AB上有三个定点C、D、E.
(1)图中共有几条线段?
(2)如果在线段CD上增加一点,则增加了几条线段?你能从中发现什么规律吗?
【答案】
解:(1)线段的条数:4+3+2+1=10(条);
(2)如果在线段CD上增加一点P,则P与其它五个点各组成一条线段,因此,增加了5条线段.
(注解:若在线段AB上增加一点,则增加2条线段,此时线段总条数为1+2;若再增加一点,则又增加了3条线段,此时线段总条数为1+2+3;…;当线段AB上增加到n个点(即增加n-2个点)时,线段的总条数为1+2+……+(n-1)=n(n-1) .)
【变式2】如图直线m上有4个点A、B、C、D,则图中共有________条射线.
【答案】8
4.(2019春?启东市月考)已知点C在线段AB上,线段AC=7cm,BC=5cm,点M、N分别是AC、BC的中点,求MN的长度.
【思路点拨】根据M、N分别为AC、BC的中点,根据AC、BC的长求出MC与CN的长,由MC+CN求出MN的长即可.
【答案与解析】
解:∵AC=7cm,BC=5cm,点M、N分别是AC、BC的中点,
∴MC=AC=3.5cm,CN=BC=2.5cm,
则MN=MC+CN=3.5+2.5=6(cm).
【总结升华】此题考查了线段的和差,熟练掌握线段中点定义是解本题的关键.
举一反三:
【变式】(2018春?淄博校级期中)如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B. 4cm C. 1cm D. 6cm
【答案】B.
解:∵点M是AC的中点,点N是BC的中点,
∴AC=2MC,BC=2NC,
∴AC﹣BC=(MC﹣NC)×2=2×2=4(cm),
即AC比BC长4cm.
类型四、最短问题
5.(2018?新疆)如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B B. A→C→F→B C. A→C→E→F→B D. A→C→M→B
【答案】B.
【解析】
根据两点之间的线段最短,
可得C、B两点之间的最短距离是线段CB的长度,
所以想尽快赶到书店,一条最近的路线是:A→C→F→B.
【总结升华】“两点之间线段最短”在实际生活中有广泛的应用,此类问题要与线段的性质联系起来,这里线段最短是指线段的长度最短,连接两点的线段的长度叫做两点间的距离,线段是图形,线段长度是数值.
举一反三:
【变式】 (1)如图1所示,把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?
(2)如图2,公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比,这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理.
【答案】
解:(1)河道的长度变小了.
(2)由于“两点之间,线段最短”,这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.
【巩固练习】
一、选择题
1.手电筒射出的光线,给我们的形象是( ).
A.直线 B.射线 C.线段 D.折线
2.下列各图中直线的表示法正确的是( ).
3.点P在线段EF上,现有四个等式①PE=PF;②PE=EF;③EF=PE;④2PE=EF;其中能表示点P是EF中点的有( ).
A.4个 B.3个 C.2个 D.1个
4.如图中分别有直线、射线、线段,能相交的是( ).
5.(2018?黄冈中学自主招生)如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点.若想求出MN的长度,那么只需条件( )
A.AB=12 B. BC=4 C. AM=5 D. CN=2
6.(2019?宜昌)如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
二、填空题
7.(2019春?威海期中)平面内不同的两点确定一条直线,不同的三点最多确定三条直线,平面内不同的六个点最多可确定 条直线.
8.在修建崇钦高速公路时,有时需要将弯曲的道路改直,依据是 .
9. 如图所示,数一数,图中共有________条线段,________条射线,________条直线,其中以B为端点的线段是________;经过点D的直线是________,可以表示出来的射线有________条.
10.如图所示,
(1)AC=BC+ ;
(2)CD=AD- ;
(3)CD= -BC;
(4)AB+BC= -CD.
11. 如图所示,直线_______和直线______相交于点P;直线AB和直线EF相交于点______;点R是直线________和直线________的交点.
12.(2018秋?太原期末)如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC= cm.
三、解答题
13.(2018秋?越秀区期末)如图,已知AB=2cm,延长线段AB至点C,使BC=2AB,点D是线段AC的中点,用刻度尺画出图形,并求线段BD的长度.
14.如图,延长线段AB到C,使,D为AC的中点,DC=2,求AB的长.
15.已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若线段AC=6,BC=4,求线段MN的长度;
(2)若AB=a,求线段MN的长度;
(3)若将(1)小题中“点C在线段AB上”改为“点C在直线AB上”,(1)小题的结果会有变化吗?求出MN的长度.
【答案与解析】
一、选择题
1.【答案】B;
【解析】手电筒本身看作射线的端点,射出的光线看作向前方无限延伸.
2.【答案】C;
【解析】要牢记直线、射线、线段的表示方法.
3.【答案】A;
【解析】点P是线段AB的中点,表示方法不唯一.
4.【答案】B;
5.【答案】A.
【解析】根据点M是线段AC的中点,点N是线段BC的中点,可知:,∴只要已知AB即可.
6.【答案】D;
【解析】解:∵用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,
∴线段AB的长小于点A绕点C到B的长度,
∴能正确解释这一现象的数学知识是两点之间,线段最短,
故选D.
二、填空题
7. 【答案】15;
【解析】解:平面内不同的六个点最多可确定 15条直线.
故答案为:15.
8. 【答案】两点之间线段最短;
【解析】线段的性质:两点之间线段最短.
9. 【答案】6 ,18, 4,线段AB、线段BC、线段BD;直线AD、直线BD、直线CD, 10;
【解析】注意利用线段、射线、直线的表示法进行区别.
10.【答案】AB, AC,BD,AD;
11.【答案】AB, CD, O, CD, EF;
12.【答案】6.
三、解答题
13.【解析】
解:如图:
,
由BC=2AB,AB=2cm,得
BC=4cm,
由线段的和差,得
AC=AB+BC=2+4=6cm,
由点D是线段AC的中点,得
AD=AC=×6=3cm.
由线段的和差,得
BD=AD﹣AB=3﹣2=1cm.
14.【解析】
解:设,则,所以有:
又∵D为线段AC的中点且
∴
解得:
所以AB的长为.
15. 【解析】
解:(1)∵ AC=6,BC=4,∴ AB=6+4=10
又∵ 点M是AC的中点,点N是BC的中点,
∴ MC=AM=AC,CN=BN=BC,
∴ MN=MC+CN=AC+BC=(AC+BC)=AB=5(cm).
(2)由(1)中已知AB=10cm求出MN=5cm,分析(1)的推算过程可知MN=AB,
故当AB=a时,MN=,
从而得到规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
(3)分类讨论:
当点C在点B的右侧时,如图可得:
;
当点C在线段AB上时,如(1);
当点C在点A的左侧时,不满足题意.
综上可得:点C在直线AB上时,MN的长为1或5.
【学习目标】
1.在现实情境中进一步理解线段、射线、直线,并会用不同的方式表示;
2. 通过操作活动,了解“两点确定一条直线”的几何事实,积累数学活动经验;
3. 能够运用几何事实解释和解决具体情境中的实际问题;
4. 通过从事观察、比较、概括等活动,发展抽象思维能力和有条理的数学表达能力.
【要点梳理】
要点一、线段、射线、直线的概念及表示方法
1.概念:绷紧的琴弦、黑板的边沿都可以近似地看作线段,如果把“线段”作为最简单、最基本原始概念,则用“线段”定义射线和直线如下:
(1)将线段向一个方向无限延长就形成了射线.
(2)将线段向两个方向无限延长就形成了直线.
要点诠释:
(1)线段有两个端点,可以度量,可以比较长短.
(2)射线只向一方无限延伸,有一个端点,不能度量,不能比较大小.
(3)直线是向两方无限延伸的,无端点,不可度量,不能比较大小.
(4)线段、射线、直线都没有粗细.
2.表示方法:如图1、图2、图3,线段、射线、直线的表示方法都有两种:它们都可以用两个大写字母表示,也可以一个小写字母表示.
要点诠释:
(1)从表示方法上看,虽然它们都可以用一个小写字母表示,也可以用两个大写字母表示,但直线取得是直线上任意两点的字母,线段用的是两个端点的字母,射线用的是一个端点和任意一点的字母,而直线和线段的两个大写字母没有顺序之分,但射线的两个大写字母有顺序之分,第一个大写字母必须是表示端点.即端点相同,而延伸方向不同,表示不同的射线.如下图4中射线OA,射线OB是不同的射线;
端点相同且延伸方向也相同的射线,表示同一条射线.如下图5中射线OA、射线OB、射线OC都表示同一条射线.
(2)表示直线、射线与线段时,勿忘在字母的前面写上“直线”“射线”“线段”字样.
3.线段、射线、直线的区别与联系
线段
射线
直线
图示
表示方法
线段AB或线段a
射线OA或射线a
直线AB或直线a
端点
两个
一个
无
长度
可度量
不可度量
不可度量
延伸性
不向两方延伸
向一方无限延伸
向两方无限延伸
要点二、基本性质
1. 直线的性质:经过两点有且只有一条直线.简单说成:两点确定一条直线.
要点诠释:
(1)点和直线的位置关系有两种:
①点在直线上,或者说直线经过这个点.如图6中,点O在直线l上,也可以说成是直线l经过点O;
②点在直线外,或者说直线不经过这个点.如图6中,点P在直线l外,也可以说直线l不经过点P.
(2)两条不同的直线相交只有一个交点.
2.线段的基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.
如图7所示,在A,B两点所连的线中,线段AB的长度是最短的.
要点诠释:
(1)连接两点间的线段的长度,叫做这两点的距离.
(2)两条线段可能无公共点,可能有一个公共点,也可能有无穷多个公共点.
要点三、比较线段的长短
1. “作一条线段等于已知线段”的两种方法:
法一:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a.
法二:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a的长度,再画一条等于这个长度的线段.
要点诠释:几何中连结两点,即画出以这两点为端点的线段.
2.线段的比较:
(1)度量法:用刻度尺量出两条线段的长度,再比较长短.
(2)叠合法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:
3.线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如下图,点C是线段AB的中点,则,或AB=2AC=2BC.
要点诠释:若点C是线段AB的中点,则点C一定在线段AB上.
【典型例题】
类型一、相关概念
1.下列说法中,正确的是( ) .
A.射线OA与射线AO是同一条射线.
B.线段AB与线段BA是同一条线段.
C.过一点只能画一条直线.
D.三条直线两两相交,必有三个交点.
【答案】B
【解析】射线OA的端点是O,射线AO的端点是A,所以射线OA与射线AO不是同一条射线,故A错误;过一点能画无数条直线,所以C错误;三条直线两两相交,有三个交点或一个交点(三条直线相交于一点时),所以D错误;线段AB与线段BA是同一条线段,所以B正确.
【总结升华】直线和线段用两个大写字母表示时,与字母的前后顺序无关,但射线必须是表示端点的字母写在前面,不能互换.
举一反三:
【变式1】以下说法中正确的是??( ).
A.延长线段AB到C B.延长射线AB
C.直线AB的端点之一是A D.延长射线OA到C
【答案】A
【变式2】如图所示,请分别指出图中的线段、射线和直线的条数,并把它们分别表示出来.
【答案】
解:如下图所示,在直线上点A左侧和点C右侧分别任取点X和Y.
图中有6条射线:射线AX、射线AY、射线BX、射线BY、射线CX、射线CY.
有3条线段:线段AB(或BA)、线段BC(或CB)、线段AC(或CA)
有1条直线:直线AC(或AB,BC).
类型二、有关作图
2.如图所示,线段a,b,且a>b.
用圆规和直尺画线段:(1)a+b;(2)a-b.
【答案与解析】
解:(1) 画法如图(1),画直线AF,在直线AF上画线段AB=a,再在AB的延长线上画线段BC=b,线段AC就是a与b的和,记作AC=a+b.
(2) 画法如图(2),画直线AF,在直线AF上画线段AB=a,再在线段AB上画线段BD=b,线段AD就是a与b的差,记作AD=a-b.
【总结升华】在画线段时,为使结果更准确,一般用直尺画直线,用圆规量取线段的长度.
举一反三:
【变式1】下列语句正确的是( ) .
A.画直线AB=10cm. B.画直线AB的垂直平分线.
C.画射线OB=3cm. D.延长线段AB到C使BC=AB.
【答案】D
【变式2】用直尺作图:P是直线a外一点,过点P有一条线段b与直线a不相交.
【答案】
解:
类型三、有关条数及长度的计算
3.如图,A、B、C、D为平面内任意三点都不在同一条直线上的四点,那么过其中两点,可画出 条直线.
【思路点拨】根据两点确定一条直线即可计算出直线的条数.
【答案】6条直线
【解析】由两点确定一条直线知,点A与B,C,D三点各确定一条直线,同理点B与C、D各确定一条直线,C与D确定一条直线,综上:共有直线:3+2+1=6(条).
【总结升华】平面上有个点,其中任意三点不在一条直线上,则最多确定的直线条数为:.
举一反三:
【变式1】如图所示,已知线段AB上有三个定点C、D、E.
(1)图中共有几条线段?
(2)如果在线段CD上增加一点,则增加了几条线段?你能从中发现什么规律吗?
【答案】
解:(1)线段的条数:4+3+2+1=10(条);
(2)如果在线段CD上增加一点P,则P与其它五个点各组成一条线段,因此,增加了5条线段.
(注解:若在线段AB上增加一点,则增加2条线段,此时线段总条数为1+2;若再增加一点,则又增加了3条线段,此时线段总条数为1+2+3;…;当线段AB上增加到n个点(即增加n-2个点)时,线段的总条数为1+2+……+(n-1)=n(n-1) .)
【变式2】如图直线m上有4个点A、B、C、D,则图中共有________条射线.
【答案】8
4.(2019春?启东市月考)已知点C在线段AB上,线段AC=7cm,BC=5cm,点M、N分别是AC、BC的中点,求MN的长度.
【思路点拨】根据M、N分别为AC、BC的中点,根据AC、BC的长求出MC与CN的长,由MC+CN求出MN的长即可.
【答案与解析】
解:∵AC=7cm,BC=5cm,点M、N分别是AC、BC的中点,
∴MC=AC=3.5cm,CN=BC=2.5cm,
则MN=MC+CN=3.5+2.5=6(cm).
【总结升华】此题考查了线段的和差,熟练掌握线段中点定义是解本题的关键.
举一反三:
【变式】(2018春?淄博校级期中)如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
A.2cm B. 4cm C. 1cm D. 6cm
【答案】B.
解:∵点M是AC的中点,点N是BC的中点,
∴AC=2MC,BC=2NC,
∴AC﹣BC=(MC﹣NC)×2=2×2=4(cm),
即AC比BC长4cm.
类型四、最短问题
5.(2018?新疆)如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B B. A→C→F→B C. A→C→E→F→B D. A→C→M→B
【答案】B.
【解析】
根据两点之间的线段最短,
可得C、B两点之间的最短距离是线段CB的长度,
所以想尽快赶到书店,一条最近的路线是:A→C→F→B.
【总结升华】“两点之间线段最短”在实际生活中有广泛的应用,此类问题要与线段的性质联系起来,这里线段最短是指线段的长度最短,连接两点的线段的长度叫做两点间的距离,线段是图形,线段长度是数值.
举一反三:
【变式】 (1)如图1所示,把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?
(2)如图2,公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比,这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理.
【答案】
解:(1)河道的长度变小了.
(2)由于“两点之间,线段最短”,这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.
【巩固练习】
一、选择题
1.手电筒射出的光线,给我们的形象是( ).
A.直线 B.射线 C.线段 D.折线
2.下列各图中直线的表示法正确的是( ).
3.点P在线段EF上,现有四个等式①PE=PF;②PE=EF;③EF=PE;④2PE=EF;其中能表示点P是EF中点的有( ).
A.4个 B.3个 C.2个 D.1个
4.如图中分别有直线、射线、线段,能相交的是( ).
5.(2018?黄冈中学自主招生)如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点.若想求出MN的长度,那么只需条件( )
A.AB=12 B. BC=4 C. AM=5 D. CN=2
6.(2019?宜昌)如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
二、填空题
7.(2019春?威海期中)平面内不同的两点确定一条直线,不同的三点最多确定三条直线,平面内不同的六个点最多可确定 条直线.
8.在修建崇钦高速公路时,有时需要将弯曲的道路改直,依据是 .
9. 如图所示,数一数,图中共有________条线段,________条射线,________条直线,其中以B为端点的线段是________;经过点D的直线是________,可以表示出来的射线有________条.
10.如图所示,
(1)AC=BC+ ;
(2)CD=AD- ;
(3)CD= -BC;
(4)AB+BC= -CD.
11. 如图所示,直线_______和直线______相交于点P;直线AB和直线EF相交于点______;点R是直线________和直线________的交点.
12.(2018秋?太原期末)如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC= cm.
三、解答题
13.(2018秋?越秀区期末)如图,已知AB=2cm,延长线段AB至点C,使BC=2AB,点D是线段AC的中点,用刻度尺画出图形,并求线段BD的长度.
14.如图,延长线段AB到C,使,D为AC的中点,DC=2,求AB的长.
15.已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若线段AC=6,BC=4,求线段MN的长度;
(2)若AB=a,求线段MN的长度;
(3)若将(1)小题中“点C在线段AB上”改为“点C在直线AB上”,(1)小题的结果会有变化吗?求出MN的长度.
【答案与解析】
一、选择题
1.【答案】B;
【解析】手电筒本身看作射线的端点,射出的光线看作向前方无限延伸.
2.【答案】C;
【解析】要牢记直线、射线、线段的表示方法.
3.【答案】A;
【解析】点P是线段AB的中点,表示方法不唯一.
4.【答案】B;
5.【答案】A.
【解析】根据点M是线段AC的中点,点N是线段BC的中点,可知:,∴只要已知AB即可.
6.【答案】D;
【解析】解:∵用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,
∴线段AB的长小于点A绕点C到B的长度,
∴能正确解释这一现象的数学知识是两点之间,线段最短,
故选D.
二、填空题
7. 【答案】15;
【解析】解:平面内不同的六个点最多可确定 15条直线.
故答案为:15.
8. 【答案】两点之间线段最短;
【解析】线段的性质:两点之间线段最短.
9. 【答案】6 ,18, 4,线段AB、线段BC、线段BD;直线AD、直线BD、直线CD, 10;
【解析】注意利用线段、射线、直线的表示法进行区别.
10.【答案】AB, AC,BD,AD;
11.【答案】AB, CD, O, CD, EF;
12.【答案】6.
三、解答题
13.【解析】
解:如图:
,
由BC=2AB,AB=2cm,得
BC=4cm,
由线段的和差,得
AC=AB+BC=2+4=6cm,
由点D是线段AC的中点,得
AD=AC=×6=3cm.
由线段的和差,得
BD=AD﹣AB=3﹣2=1cm.
14.【解析】
解:设,则,所以有:
又∵D为线段AC的中点且
∴
解得:
所以AB的长为.
15. 【解析】
解:(1)∵ AC=6,BC=4,∴ AB=6+4=10
又∵ 点M是AC的中点,点N是BC的中点,
∴ MC=AM=AC,CN=BN=BC,
∴ MN=MC+CN=AC+BC=(AC+BC)=AB=5(cm).
(2)由(1)中已知AB=10cm求出MN=5cm,分析(1)的推算过程可知MN=AB,
故当AB=a时,MN=,
从而得到规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
(3)分类讨论:
当点C在点B的右侧时,如图可得:
;
当点C在线段AB上时,如(1);
当点C在点A的左侧时,不满足题意.
综上可得:点C在直线AB上时,MN的长为1或5.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
