3.2.1 对数及其运算 18张
文档属性
| 名称 | 3.2.1 对数及其运算 18张 |

|
|
| 格式 | zip | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
一、导入
口算下列各式:
1
2
3
4
?
对数
对数与对数运算
二、探究学习
探究一:对数的概念
思考:已知底数和幂的值,怎样求指数呢?例如:由 ,求 .
探究一:对数的概念
一般地,如果 ,那么数__ 叫做以__为底__的对数,记做 _______.
叫做对数的____, 叫做_____.
注意:
(1)底数的限制:
(2)对数的书写格式:
底数
真数
(为什么?)
试一试:
(1) 表示2是以___为底,___的对数;
(2) 表示3是以___为底,____的对数。
探究一:对数的概念
4
16
2
8
思考:从对数的概念中我们发现,对数是从指数引申而来的,那么指数式和对数式之间有什么关系呢?
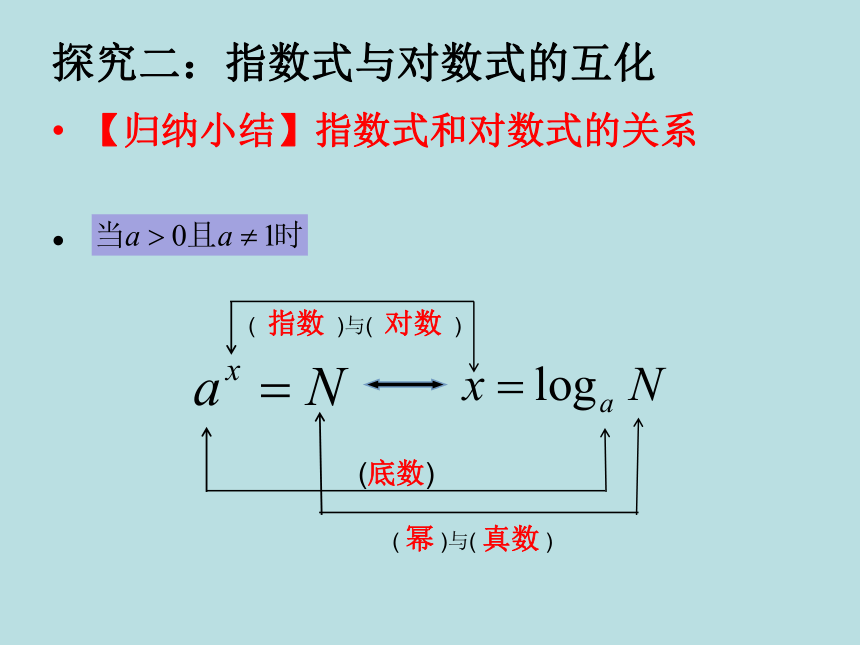
探究二:指数式与对数式的互化
【归纳小结】指数式和对数式的关系
探究二:指数式与对数式的互化
( 指数 )与( 对数 )
(底数)
( 幂 )与( 真数 )
【特殊对数】
(1)常用对数,以10为底的对数,把 记为__________
(2)自然对数,以无理数 为底数的对数,把 记为_________
探究二:指数式与对数式的互化
例题讲解
例1 将下列指数式写成对数式或对数式写成指数式:
思考1:当 时,
则:
思考2:负数和零有没有对数?为什么?
探究三:对数的基本性质
【归纳小结】对数的性质:
(1)_____和_____没有对数.
(2) ; ( ).
探究三:对数的基本性质
负数 零
0
1
例2 计算下列各式中 的值:
例题讲解
求下列各式中 的值:
思考:
=3
=89
探究四:对数恒等式
【归纳小结】对数恒等式:
例3:(1)
(2)
10
6
学习小结
1.对数的概念
2.指数式与对数式的关系[当 时, .]
3.对数的性质:基本性质&对数恒等式
1.将下列指数式写成对数式或对数式写成指数式:
当堂检测
2.求下列各式中 的值:
当堂检测
课后作业
完成导学案【模块六:课后作业】
一、导入
口算下列各式:
1
2
3
4
?
对数
对数与对数运算
二、探究学习
探究一:对数的概念
思考:已知底数和幂的值,怎样求指数呢?例如:由 ,求 .
探究一:对数的概念
一般地,如果 ,那么数__ 叫做以__为底__的对数,记做 _______.
叫做对数的____, 叫做_____.
注意:
(1)底数的限制:
(2)对数的书写格式:
底数
真数
(为什么?)
试一试:
(1) 表示2是以___为底,___的对数;
(2) 表示3是以___为底,____的对数。
探究一:对数的概念
4
16
2
8
思考:从对数的概念中我们发现,对数是从指数引申而来的,那么指数式和对数式之间有什么关系呢?
探究二:指数式与对数式的互化
【归纳小结】指数式和对数式的关系
探究二:指数式与对数式的互化
( 指数 )与( 对数 )
(底数)
( 幂 )与( 真数 )
【特殊对数】
(1)常用对数,以10为底的对数,把 记为__________
(2)自然对数,以无理数 为底数的对数,把 记为_________
探究二:指数式与对数式的互化
例题讲解
例1 将下列指数式写成对数式或对数式写成指数式:
思考1:当 时,
则:
思考2:负数和零有没有对数?为什么?
探究三:对数的基本性质
【归纳小结】对数的性质:
(1)_____和_____没有对数.
(2) ; ( ).
探究三:对数的基本性质
负数 零
0
1
例2 计算下列各式中 的值:
例题讲解
求下列各式中 的值:
思考:
=3
=89
探究四:对数恒等式
【归纳小结】对数恒等式:
例3:(1)
(2)
10
6
学习小结
1.对数的概念
2.指数式与对数式的关系[当 时, .]
3.对数的性质:基本性质&对数恒等式
1.将下列指数式写成对数式或对数式写成指数式:
当堂检测
2.求下列各式中 的值:
当堂检测
课后作业
完成导学案【模块六:课后作业】
