3.3 幂函数 38张

(共38张PPT)
幂函数
其中x是自变量，函数定义域是 _____.

1.指数函数：形如
的函数叫做
指数函数。
回顾
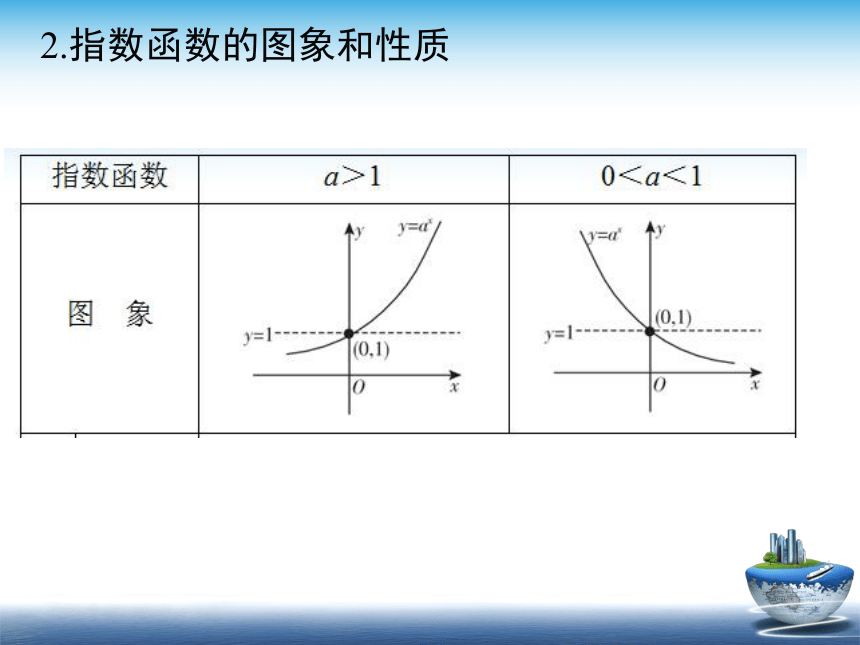
2.指数函数的图象和性质
引 入
我们先来看看几个具体的问题:
(1)如果张红买了每千克1元的蔬菜w千克,那么她需要支付
__________

P=w 元
(2)如果正方形的边长为 a,那么正方形的面积__ ___
(3)如果立方体的边长为 a,那么立方体的体积_________

(4)如果某人 t s内骑车行进1 km,那么他骑车的平均速度____________


P是w的函数
S=a?
S 是a的函数
V=a?
V是a的函数
V=t?? km/s
V是t 的函数
(5) 如果一个正方形场地的面积为S，那么这个

正方形的边长
a是S的函数

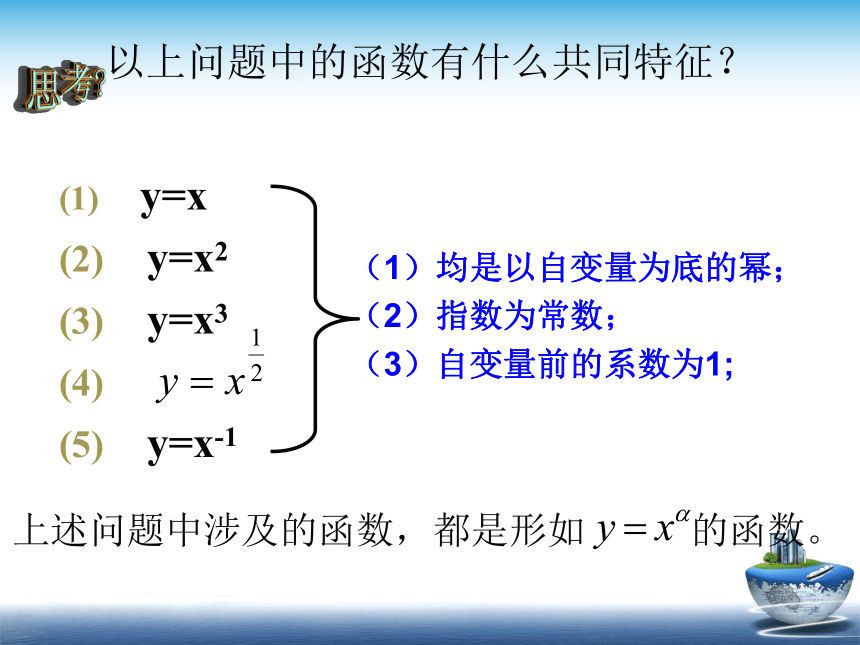
以上问题中的函数有什么共同特征？
（1）均是以自变量为底的幂；
（2）指数为常数；
（3）自变量前的系数为1;
上述问题中涉及的函数，都是形如 的函数。
　y=x
　y=x2
　y=x3
　
　y=x-1


幂函数的定义
一般地，形如 的函数叫做幂函数，其中 是常数
1.判断下列函数是否为幂函数.
(1) y=x4
(3) y= -x2
(5) y=2x2
(6) y=x3+2






做一做


系数只能为1

常数
底数是自变量x
对比 底数 指数
幂函数 y=xa
指数函数 y=ax
自变量x
常数a
常数a
自变量x
求幂函数的解析式
幂函数的性质

我们重点研究
课堂实验
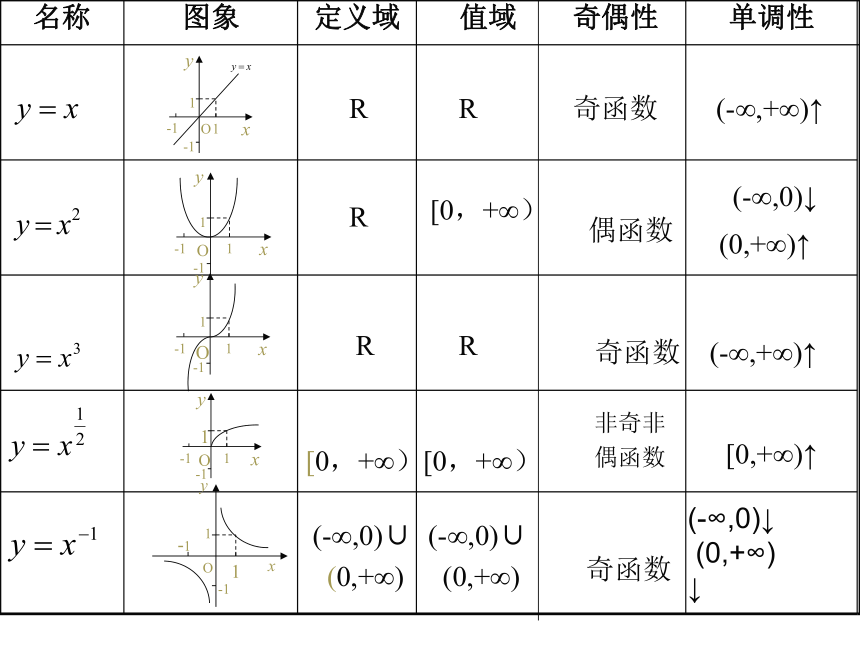
名称 图象 定义域 值域 奇偶性 单调性








O
x
y


1
1




-1

-1


O
x
y


1
1



-1

-1



O
x
y


1
1



-1

-1




O
x
y


1
1



-1

-1

R
R
R
[0，+∞）

奇函数
偶函数
奇函数
非奇非
偶函数
奇函数
(0,+∞)↑
(-∞,0)↓
(-∞,+∞)↑
(-∞,+∞)↑
[0,+∞)↑
(-∞,0)↓
(0,+∞) ↓



O
x
y


1
1



-1

-1


(-∞,0)∪
(0,+∞)

R
[0，+∞）
[0，+∞）
(-∞,0)∪
(0,+∞)
R
观察这5个幂函数的图象，有共同的特征吗？有哪些共同特征呢？
思考
1.幂函数有定点吗？定点坐标呢？
2.所有幂函数恒过哪个象限？
3.每个幂函数都过原点吗？
第一象限中，幂函数的单调性有什么共同的特征？
有哪些幂函数是增函数？哪些是减函数？
有，（1，1）
第一象限
即所有幂函数在(0，＋∞)上都有定义
思考
如果a＞0，幂函数在x＝0处有意义，且
在(0，＋∞)上是增函数.
如果a＜0，幂函数在x＝0处无意义，且
在(0，＋∞)上是减函数.
课堂实验
求幂函数的解析式
D
比较幂的大小
【小结】
1.比较幂值的大小，关键在于构造适当的函数：(1)若指数相同而底数不同，则构造幂函数；
(2)若指数不同而底数相同，则构造指数函数.
2.若指数与底数都不同，需考虑是否能把指数或底数化为相同，是否可以引入中间量.
课堂小结
1. 幂函数的定义 2. 幂函数的性质 3. 渗透的数学思想：

4. 渗透的数学素养：
数形结合，类比思想，从特殊到一般
数学抽象，数学运算
C
C
幂函数的图象


【方法规律】幂函数图象的特征：(1)在第一象限内，直线x＝1的右侧，y＝xα的图象由上到下，指数α由大变小；在第一象限内，直线x＝1的左侧，y＝xα的图象由上到下，指数α由小变大.(2)当α＞0时，幂函数的图象都经过(0,0)和(1,1)点，在第一象限内，当0＜α＜1时，曲线上凸；当α＞1时，曲线下凸.当α＜0时，幂函数的图象都经过(1,1)点，在第一象限内，曲线下凸.
2.已知函数y＝xa，y＝xb，y＝xc的图象如图所示，则a，b，c的大小关系为(　　)
A．cB．aC．bD．c【答案】A
【解析】由幂函数的图象特征知，c<0，a>1，0＜b＜1.所以c
比较幂的大小
【方法规律】1.比较幂值的大小，关键在于构造适当的函数：(1)若指数相同而底数不同，则构造幂函数；(2)若指数不同而底数相同，则构造指数函数.
2.若指数与底数都不同，需考虑是否能把指数或底数化为相同，是否可以引入中间量.
幂函数性质理解不透致误
【警示】本题从幂函数的概念、图象，单调性以及奇偶性来考查，综合性较强，解题的关键是准确把握幂函数的图象，抓住了幂函数的图象就抓住了性质，也就有效地解决了应用中的困难.
小结
(1) 幂函数的定义；
(2) 幂函数的性质；
(3) 利用幂函数的单调性判别大小
作业：习题2.3 第 1题。课本P82 第10题