人教A版高中数学必修二:1.1空间几何体的结构特征教案
文档属性
| 名称 | 人教A版高中数学必修二:1.1空间几何体的结构特征教案 |  | |
| 格式 | zip | ||
| 文件大小 | 553.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 09:28:15 | ||
图片预览

文档简介
棱柱、棱锥、棱台的结构特征 教案
【教学目标】
1.会用语言概述棱柱、棱锥、棱台的结构特征。
2.能根据几何结构特征对空间物体进行分类。
3.提高学生的观察能力;培养学生的空间想象能力和抽象括能力。
【教学重难点】
教学重点:让学生感受大量空间实物及模型、概括出柱、锥、台的结构特征。
教学难点:柱、锥、台的结构特征的概括。
【课型】新授课、合作探究课
【教学学法】 任务驱动法,自主探究合作交流
教学过程
一、引入:
小学和初中我们学过平面上的一些几何图形如直线、三角形、长方形、圆等等,现实生活中,我们周围还存在着很多不是平面上而是“空间”中的物体,它们占据着空间的一部分,比如粉笔盒、足球、易拉罐等.如果只考虑这些物体的形状和大小,那么由这些物体抽象出来的空间图形叫做空间几何体.从航空测绘到土木建筑以至家具装潢,空间图形与我们的生活息息相关,它们具有千姿百态的形状,有着不同的几何特征,现在就让我们来研究它们吧!
新课
※ 探索新知
问题1:多面体的相关概念
问题:观察下面的物体,注意它们每个面的特点,以及面与面之间的关系.你能说出它们相同点吗?
新知1:由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面,如面ABCD;相邻两个面的公共边叫多面体的棱,如棱AB;棱与棱的公共点叫多面体的顶点,如顶点A.具体如下图所示:
( 1 )
问题2:旋转体的相关概念
问题:仔细观察下列物体的相同点是什么?
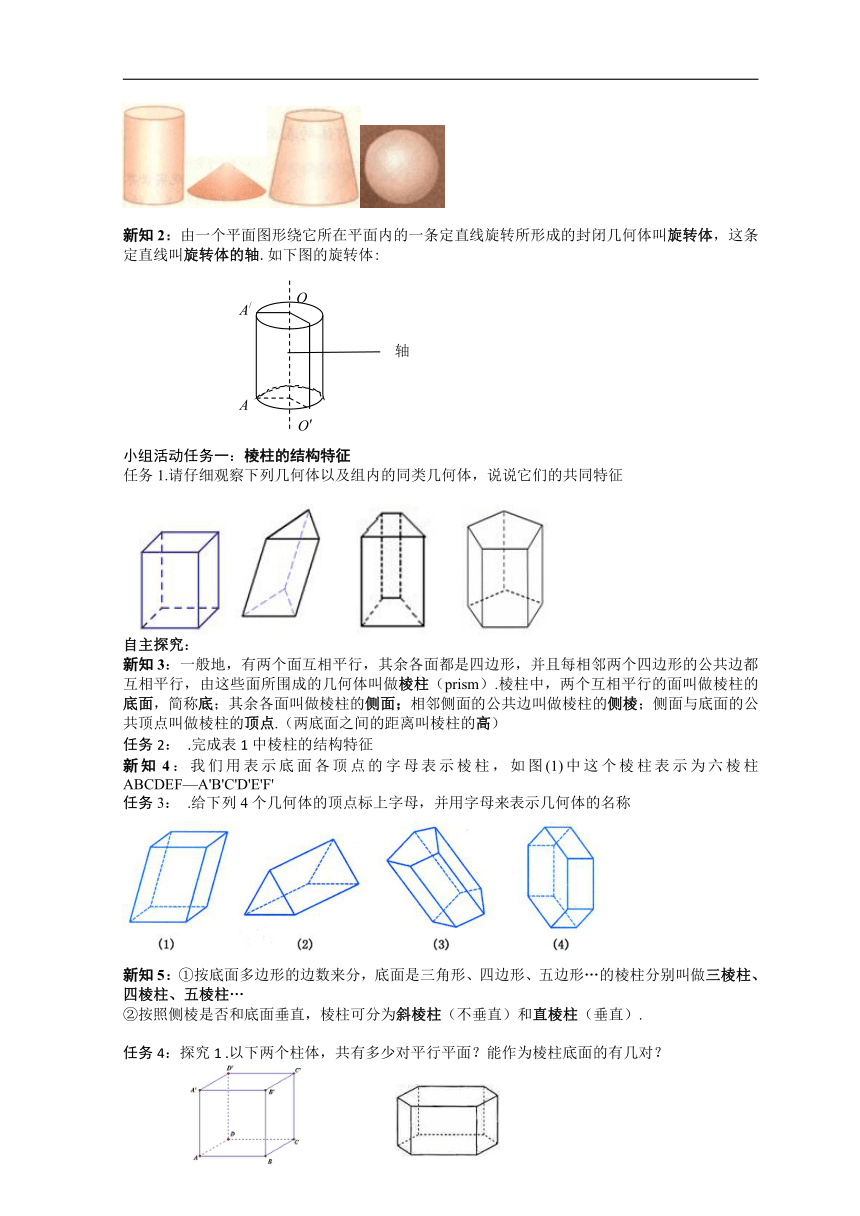
新知2:由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫旋转体,这条定直线叫旋转体的轴.如下图的旋转体:
小组活动任务一:棱柱的结构特征
任务1.请仔细观察下列几何体以及组内的同类几何体,说说它们的共同特征
自主探究:
新知3:一般地,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱(prism).棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.(两底面之间的距离叫棱柱的高)
任务2: .完成表1中棱柱的结构特征
新知4:我们用表示底面各顶点的字母表示棱柱,如图(1)中这个棱柱表示为六棱柱ABCDEF—A'B'C'D'E'F'
任务3: .给下列4个几何体的顶点标上字母,并用字母来表示几何体的名称
新知5:①按底面多边形的边数来分,底面是三角形、四边形、五边形…的棱柱分别叫做三棱柱、四棱柱、五棱柱…
②按照侧棱是否和底面垂直,棱柱可分为斜棱柱(不垂直)和直棱柱(垂直).
任务4:探究1 .以下两个柱体,共有多少对平行平面?能作为棱柱底面的有几对?
探究2. 长方体按如图截去一角,其中EH//BC,剩下所得的两部分还是棱柱吗?请说出它们的名称
补充:几种四棱柱(六面体)的关系:
小组活动任务二:棱锥的结构特征
任务1:请仔细观察下列几何体以及组内的同类几何体,说说它们的共同特点。
自主探究:
新知6:有一个面是多边形,其余各个面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.顶点到底面的距离叫做棱锥的高;棱锥也可以按照底面的边数分为三棱锥(四面体)、四棱锥…等等,棱锥可以用顶点和底面各顶点的字母表示,如下图中的棱锥.
任务2:完成表1中棱锥的结构特征
任务3:观察下列正棱锥,有什么特征?
任务4:观察正三棱锥与正四面体,它们有何区别和联系?
小组活动任务三:棱台的结构特征
任务1:请仔细观察下列几何体以及组内的同类几何体,说说它们的共同特征。
自主探究:
新知7:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分形成的几何体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面.其余各面是棱台的侧面,相邻侧面的公共边叫侧棱,侧面与两底面的公共点叫顶点.两底面间的距离叫棱台的高.棱台可以用上、下底面的字母表示,分类类似于棱锥.
任务2:完成表1中棱台的结构特征
任务3:试一试,右边几何体是不是棱台,为什么?
反思:根据结构特征,从变化的角度想一想,棱柱、棱台、棱锥三者之间有什么关系?
任务4思考:既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?
三、总结提升
1. 多面体、旋转体的有关概念;
2. 棱柱、棱锥、棱台的结构特征及简单的几何性质.
四、作业
课时作业1
※ 知识拓展
1. 平行六面体:底面是平行四边形的四棱柱;
2. 正棱柱:底面是正多边形的直棱柱;
3. 正棱锥:底面是正多边形并且顶点在底面的射影是底面正多边形中心的棱锥;
4. 正棱台:由正棱锥截得的棱台叫做正棱台.
板书设计:
空间几何体的结构特征
1.空间几何体
2.多面体 旋转体
3棱柱 棱锥 棱台的结构特征
表1
结构特征
棱柱
棱锥
棱台
底面
侧面
侧棱
平行于底面
的截面
【教学目标】
1.会用语言概述棱柱、棱锥、棱台的结构特征。
2.能根据几何结构特征对空间物体进行分类。
3.提高学生的观察能力;培养学生的空间想象能力和抽象括能力。
【教学重难点】
教学重点:让学生感受大量空间实物及模型、概括出柱、锥、台的结构特征。
教学难点:柱、锥、台的结构特征的概括。
【课型】新授课、合作探究课
【教学学法】 任务驱动法,自主探究合作交流
教学过程
一、引入:
小学和初中我们学过平面上的一些几何图形如直线、三角形、长方形、圆等等,现实生活中,我们周围还存在着很多不是平面上而是“空间”中的物体,它们占据着空间的一部分,比如粉笔盒、足球、易拉罐等.如果只考虑这些物体的形状和大小,那么由这些物体抽象出来的空间图形叫做空间几何体.从航空测绘到土木建筑以至家具装潢,空间图形与我们的生活息息相关,它们具有千姿百态的形状,有着不同的几何特征,现在就让我们来研究它们吧!
新课
※ 探索新知
问题1:多面体的相关概念
问题:观察下面的物体,注意它们每个面的特点,以及面与面之间的关系.你能说出它们相同点吗?
新知1:由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面,如面ABCD;相邻两个面的公共边叫多面体的棱,如棱AB;棱与棱的公共点叫多面体的顶点,如顶点A.具体如下图所示:
( 1 )
问题2:旋转体的相关概念
问题:仔细观察下列物体的相同点是什么?
新知2:由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫旋转体,这条定直线叫旋转体的轴.如下图的旋转体:
小组活动任务一:棱柱的结构特征
任务1.请仔细观察下列几何体以及组内的同类几何体,说说它们的共同特征
自主探究:
新知3:一般地,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱(prism).棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.(两底面之间的距离叫棱柱的高)
任务2: .完成表1中棱柱的结构特征
新知4:我们用表示底面各顶点的字母表示棱柱,如图(1)中这个棱柱表示为六棱柱ABCDEF—A'B'C'D'E'F'
任务3: .给下列4个几何体的顶点标上字母,并用字母来表示几何体的名称
新知5:①按底面多边形的边数来分,底面是三角形、四边形、五边形…的棱柱分别叫做三棱柱、四棱柱、五棱柱…
②按照侧棱是否和底面垂直,棱柱可分为斜棱柱(不垂直)和直棱柱(垂直).
任务4:探究1 .以下两个柱体,共有多少对平行平面?能作为棱柱底面的有几对?
探究2. 长方体按如图截去一角,其中EH//BC,剩下所得的两部分还是棱柱吗?请说出它们的名称
补充:几种四棱柱(六面体)的关系:
小组活动任务二:棱锥的结构特征
任务1:请仔细观察下列几何体以及组内的同类几何体,说说它们的共同特点。
自主探究:
新知6:有一个面是多边形,其余各个面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.顶点到底面的距离叫做棱锥的高;棱锥也可以按照底面的边数分为三棱锥(四面体)、四棱锥…等等,棱锥可以用顶点和底面各顶点的字母表示,如下图中的棱锥.
任务2:完成表1中棱锥的结构特征
任务3:观察下列正棱锥,有什么特征?
任务4:观察正三棱锥与正四面体,它们有何区别和联系?
小组活动任务三:棱台的结构特征
任务1:请仔细观察下列几何体以及组内的同类几何体,说说它们的共同特征。
自主探究:
新知7:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分形成的几何体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面.其余各面是棱台的侧面,相邻侧面的公共边叫侧棱,侧面与两底面的公共点叫顶点.两底面间的距离叫棱台的高.棱台可以用上、下底面的字母表示,分类类似于棱锥.
任务2:完成表1中棱台的结构特征
任务3:试一试,右边几何体是不是棱台,为什么?
反思:根据结构特征,从变化的角度想一想,棱柱、棱台、棱锥三者之间有什么关系?
任务4思考:既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?
三、总结提升
1. 多面体、旋转体的有关概念;
2. 棱柱、棱锥、棱台的结构特征及简单的几何性质.
四、作业
课时作业1
※ 知识拓展
1. 平行六面体:底面是平行四边形的四棱柱;
2. 正棱柱:底面是正多边形的直棱柱;
3. 正棱锥:底面是正多边形并且顶点在底面的射影是底面正多边形中心的棱锥;
4. 正棱台:由正棱锥截得的棱台叫做正棱台.
板书设计:
空间几何体的结构特征
1.空间几何体
2.多面体 旋转体
3棱柱 棱锥 棱台的结构特征
表1
结构特征
棱柱
棱锥
棱台
底面
侧面
侧棱
平行于底面
的截面
