沪科版数学七年上册1.5有理数的乘法课件(23张PPT)
文档属性
| 名称 | 沪科版数学七年上册1.5有理数的乘法课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 946.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览

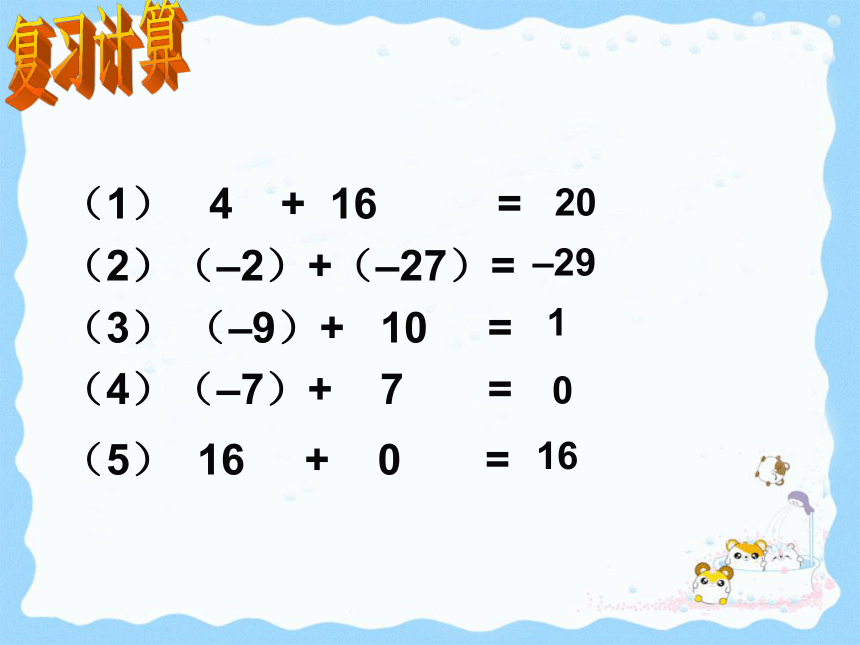





文档简介
课件23张PPT。有理数的乘法
(1) 4 + 16 =
(2)(–2)+(–27)=
(3) (–9)+ 10 =
(4)(–7)+ 7 =
(5) 16 + 0 =
20–291160复习计算计算(1)3+3+3=
(2)(-4)+(-4)+(-4)= 你能将以上两个算式写成乘法公式吗?2、如果3分钟以后记为+3分钟,那么3
分钟以前应该记为 。 1、如果一只蜗牛向右爬行2cm记为+2cm,
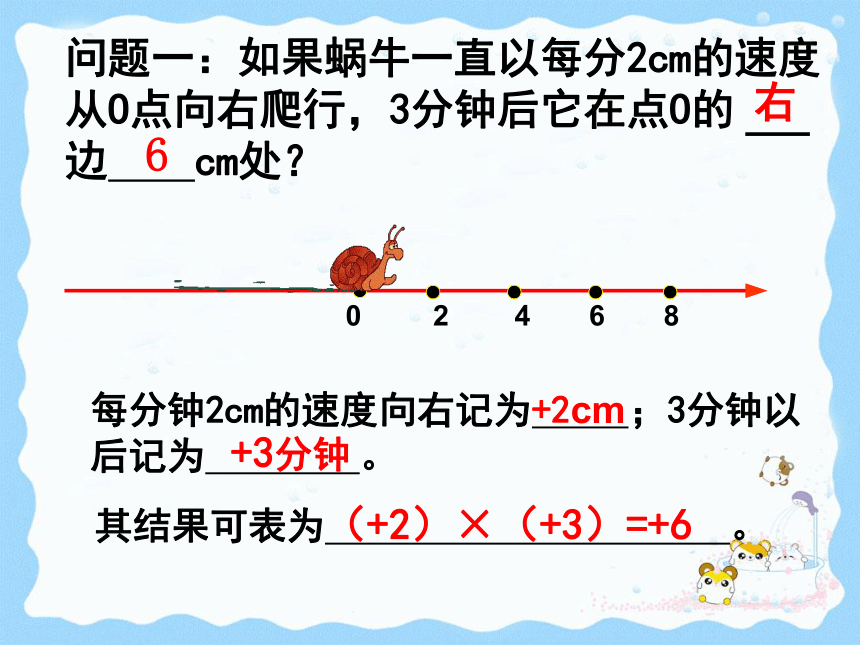
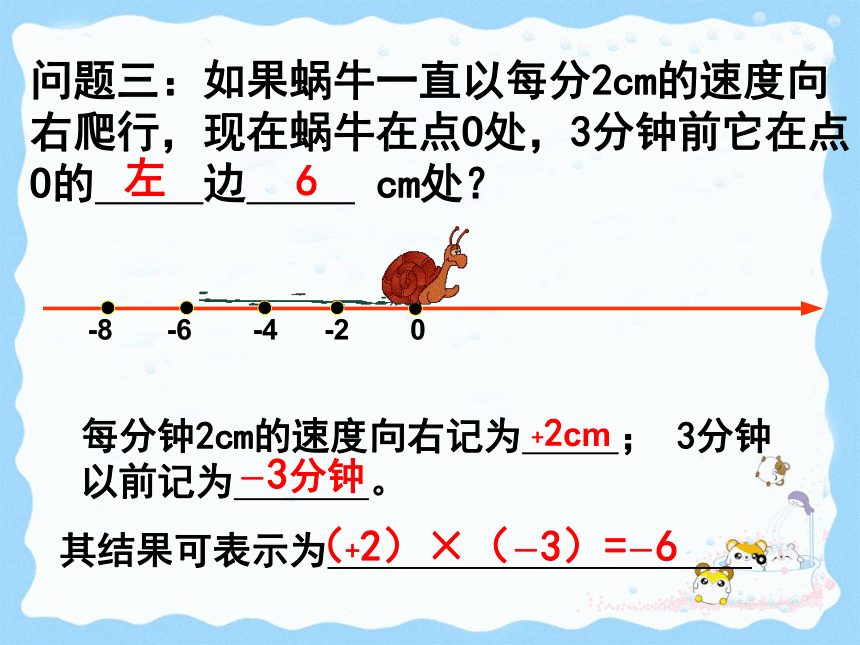
那么向左爬行2cm应该记为 。 -2cm-3分钟复习回顾如图,有一只蜗牛沿直线l爬行,它现在的位置恰好在l上的一点O。0右6+2cm+3分钟(+2)×(+3)=+60左6-2cm+3分钟(-2)×(+3)=-6问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在点O处,3分钟前它在点O的 边 cm处?0左6每分钟2cm的速度向右记为 ; 3分钟以前记为 。其结果可表示为 。+2cm-3分钟(+2)×(-3)=-6问题四:如果蜗牛一直以每分2cm的速度向左爬行,现在蜗牛在点O处,3分钟前它在点O 边 cm处?0右6每分钟2cm的速度向左记为 ; 3分钟以前记为 。其结果可表示为 。-2cm-3分钟(-2)×(-3)=+6观察这四个式子:
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数;负数乘负数积为__数;
负数乘正数积为__数;正数乘负数积为__数;
乘积的绝对值等于各因数绝对值的__。正正负负积?思考:当一个因数为0时,积是多少?(同号得正)(异号得负)如(-2)×0=0×3=00有理数乘法法则两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。法则的应用:(-5)×(-3)(-7)×4= += 15(5 × 3)= -(7 × 4)= -28有理数相乘,先确定积的符号,再确定积的绝对值。例1 计算:(1)(-5) × (-6)(2)(- )×(3)(- )× (- )(4) 8 × (-1.25)
观察上面两题有何特点?总结:有理数中仍然有:乘积是1的两个数互为倒数 数a(a≠0)的倒数是什么?(2)(- )×(-2)=1解:(1) ×2 = 1例2 计算:
(1) ×2 (2) (- ) × ( -2 )(a≠0时,a的倒数是 )1-13-3-3-3小试牛刀正数的倒数是正数负数的倒数是负数互为倒数的两个数积为1 例3:
用正负数表示气温的变化量,上升为正,
下降为负,登山队攀登一座山峰,每登高
1km气温的变化量为-6 0C,攀登3km后,
气温有什么变化?商店降价销售某种商品,每件降5元,
售出60件后,与按原价销售同样数量
的商品相比,销售额有什么变化?解:(-5)×60 =-300
答:销售额减少300元。再试牛刀(1) 若 ab>0,则必有 ( )A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0(2)若ab=0,则一定有( ) a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0DB三思而行C三思而行2±1(6)两个有理数的积为正数,和为负数,
则这两个有理数( )
A、一正一负 B、都是正数
C、都是负数 D、不能确定C链接中考已知a、b互为相反数,c、d互为倒数,
求 的值。 通过本节课的学习,大家有
什么收获呢?
小结做一做1.课堂作业:课本37页习题1.3.
2.预习作业:预习课本31页至32页.
想一想:
(1) 三个或三个以上不等于零的有理数相乘时,积的符号如何决定?
(2)在有理数运算中,乘法的交换律,结合律以及分配律还成立吗?
(1) 4 + 16 =
(2)(–2)+(–27)=
(3) (–9)+ 10 =
(4)(–7)+ 7 =
(5) 16 + 0 =
20–291160复习计算计算(1)3+3+3=
(2)(-4)+(-4)+(-4)= 你能将以上两个算式写成乘法公式吗?2、如果3分钟以后记为+3分钟,那么3
分钟以前应该记为 。 1、如果一只蜗牛向右爬行2cm记为+2cm,
那么向左爬行2cm应该记为 。 -2cm-3分钟复习回顾如图,有一只蜗牛沿直线l爬行,它现在的位置恰好在l上的一点O。0右6+2cm+3分钟(+2)×(+3)=+60左6-2cm+3分钟(-2)×(+3)=-6问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在点O处,3分钟前它在点O的 边 cm处?0左6每分钟2cm的速度向右记为 ; 3分钟以前记为 。其结果可表示为 。+2cm-3分钟(+2)×(-3)=-6问题四:如果蜗牛一直以每分2cm的速度向左爬行,现在蜗牛在点O处,3分钟前它在点O 边 cm处?0右6每分钟2cm的速度向左记为 ; 3分钟以前记为 。其结果可表示为 。-2cm-3分钟(-2)×(-3)=+6观察这四个式子:
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数;负数乘负数积为__数;
负数乘正数积为__数;正数乘负数积为__数;
乘积的绝对值等于各因数绝对值的__。正正负负积?思考:当一个因数为0时,积是多少?(同号得正)(异号得负)如(-2)×0=0×3=00有理数乘法法则两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。法则的应用:(-5)×(-3)(-7)×4= += 15(5 × 3)= -(7 × 4)= -28有理数相乘,先确定积的符号,再确定积的绝对值。例1 计算:(1)(-5) × (-6)(2)(- )×(3)(- )× (- )(4) 8 × (-1.25)
观察上面两题有何特点?总结:有理数中仍然有:乘积是1的两个数互为倒数 数a(a≠0)的倒数是什么?(2)(- )×(-2)=1解:(1) ×2 = 1例2 计算:
(1) ×2 (2) (- ) × ( -2 )(a≠0时,a的倒数是 )1-13-3-3-3小试牛刀正数的倒数是正数负数的倒数是负数互为倒数的两个数积为1 例3:
用正负数表示气温的变化量,上升为正,
下降为负,登山队攀登一座山峰,每登高
1km气温的变化量为-6 0C,攀登3km后,
气温有什么变化?商店降价销售某种商品,每件降5元,
售出60件后,与按原价销售同样数量
的商品相比,销售额有什么变化?解:(-5)×60 =-300
答:销售额减少300元。再试牛刀(1) 若 ab>0,则必有 ( )A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0(2)若ab=0,则一定有( ) a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0DB三思而行C三思而行2±1(6)两个有理数的积为正数,和为负数,
则这两个有理数( )
A、一正一负 B、都是正数
C、都是负数 D、不能确定C链接中考已知a、b互为相反数,c、d互为倒数,
求 的值。 通过本节课的学习,大家有
什么收获呢?
小结做一做1.课堂作业:课本37页习题1.3.
2.预习作业:预习课本31页至32页.
想一想:
(1) 三个或三个以上不等于零的有理数相乘时,积的符号如何决定?
(2)在有理数运算中,乘法的交换律,结合律以及分配律还成立吗?
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
