北师大版初中数学八年级上册第11讲 平面直角坐标系(基础)(知识讲解+巩固练习)
文档属性
| 名称 | 北师大版初中数学八年级上册第11讲 平面直角坐标系(基础)(知识讲解+巩固练习) |

|
|
| 格式 | zip | ||
| 文件大小 | 371.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-18 23:09:51 | ||
图片预览



文档简介
平面直角坐标系(基础)
【学习目标】
1.了解确定位置的方法,用有序数对或用方向和距离来确定物体的位置.
2.理解平面直角坐标系概念,能正确画出平面直角坐标系.
2.能在平面直角坐标系中,根据坐标描出点的位置、由点的位置写出它的坐标.
3.会用确定坐标、描点、连线的方法在直角坐标系中作出简单图形.
【要点梳理】
要点一、确定位置的方法
有序数对:把有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b).
要点诠释:
有序,即两个数的位置不能随意交换,(a,b)与(b,a)顺序不同,含义就不同,如电影院的座位是6排7号,可以写成(6,7)的形式,而(7,6)则表示7排6号.
可以用有序数对确定物体的位置,也可以用方向和距离来确定物体的位置(或称方位).
要点二、平面直角坐标系与点的坐标的概念
1.平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系.水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点(如图1).
要点诠释:平面直角坐标系是由两条互相垂直且有公共原点的数轴组成的.
2.点的坐标
平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标,记作:P(a,b),如图2.
要点诠释:
(1)表示点的坐标时,约定横坐标写在前,纵坐标写在后,中间用“,”隔开.
(2)点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离.
(3) 对于坐标平面内任意一点都有唯一的一对有序数对(x,y)和它对应,反过来对于任意一对有序数对,在坐标平面内都有唯一的一点与它对应,也就是说,坐标平面内的点与有序数对是一一对应的.
要点三、坐标平面
1. 象限
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限和第四象限,如下图.
要点诠释:
(1)坐标轴x轴与y轴上的点(包括原点)不属于任何象限.
(2)按方位来说:第一象限在坐标平面的右上方,第二象限在左上方,第三象限在左下方,第四象限在右下方.
2.各个象限内和坐标轴上点的坐标的符号特征
要点诠释:
(1)对于坐标平面内任意一个点,不在这四个象限内,就在坐标轴上.
(2)坐标轴上点的坐标特征:x轴上的点的纵坐标为0;y轴上的点的横坐标为0.
(3)根据点的坐标的符号情况可以判断点在坐标平面上的大概位置;反之,根据点在坐标平面上的位置也可以判断点的坐标的符号情况.
【典型例题】
类型一、确定物体的位置
1.如果将一张“13排10号”的电影票简记为(13,10),那么(10,13)表示的电影票是 排 号.
【思路点拨】在平面上,一个数据不能确定平面上点的位置.须用有序数对来表示平面内点的位置.
【答案】10,13.
【解析】由条件可知:前面的数表示排数,后面的数表示号数.
【总结升华】在表示时,先要“约定”顺序,一旦顺序“约定”,两个数的位置就不能随意交换,(a,b)与(b,a)顺序不同,含义就不同.
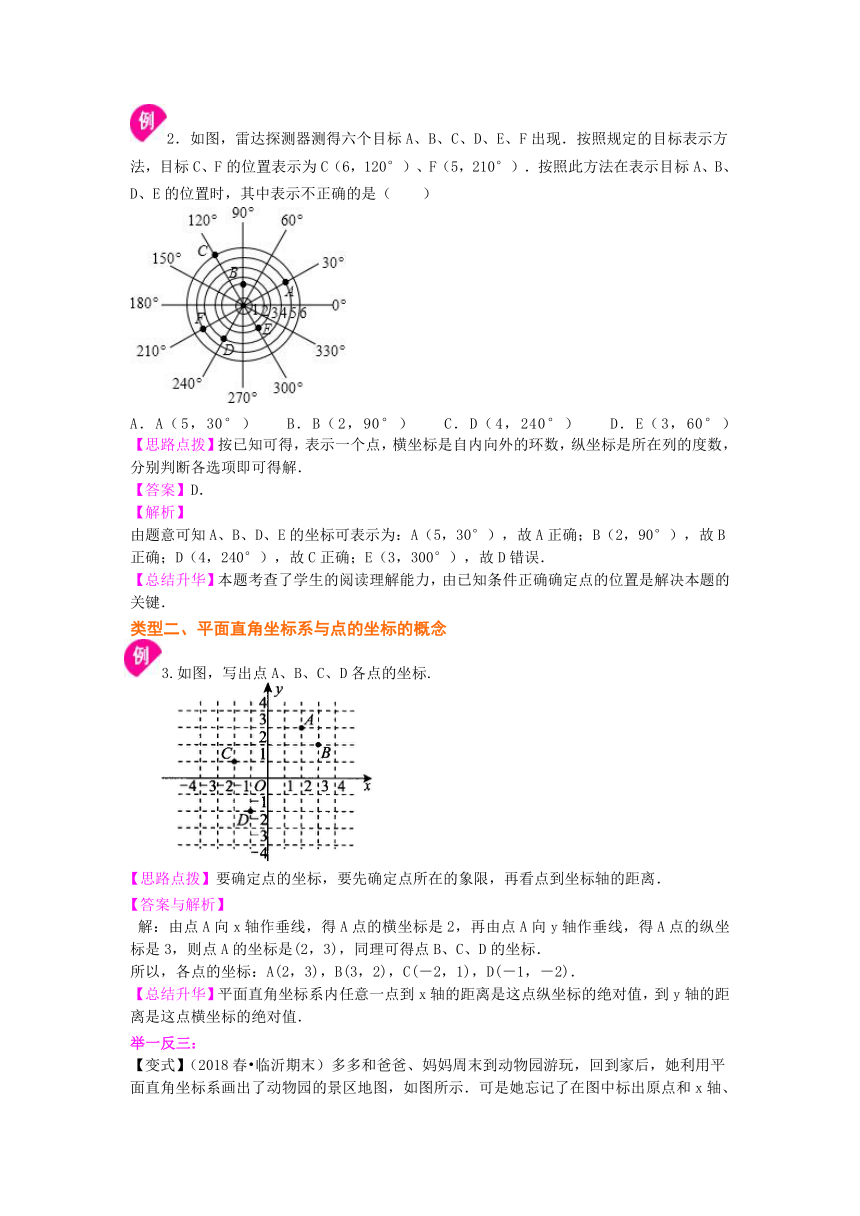
2.如图,雷达探测器测得六个目标A、B、C、D、E、F出现.按照规定的目标表示方法,目标C、F的位置表示为C(6,120°)、F(5,210°).按照此方法在表示目标A、B、D、E的位置时,其中表示不正确的是( )
A.A(5,30°) B.B(2,90°) C.D(4,240°) D.E(3,60°)
【思路点拨】按已知可得,表示一个点,横坐标是自内向外的环数,纵坐标是所在列的度数,分别判断各选项即可得解.
【答案】D.
【解析】
由题意可知A、B、D、E的坐标可表示为:A(5,30°),故A正确;B(2,90°),故B正确;D(4,240°),故C正确;E(3,300°),故D错误.
【总结升华】本题考查了学生的阅读理解能力,由已知条件正确确定点的位置是解决本题的关键.
类型二、平面直角坐标系与点的坐标的概念
3.如图,写出点A、B、C、D各点的坐标.
【思路点拨】要确定点的坐标,要先确定点所在的象限,再看点到坐标轴的距离.
【答案与解析】
解:由点A向x轴作垂线,得A点的横坐标是2,再由点A向y轴作垂线,得A点的纵坐标是3,则点A的坐标是(2,3),同理可得点B、C、D的坐标.
所以,各点的坐标:A(2,3),B(3,2),C(-2,1),D(-1,-2).
【总结升华】平面直角坐标系内任意一点到x轴的距离是这点纵坐标的绝对值,到y轴的距离是这点横坐标的绝对值.
举一反三:
【变式】(2018春?临沂期末)多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道马场的坐标为(﹣3,﹣3),你能帮她建立平面直角坐标系并求出其他各景点的坐标?
【答案】解:建立坐标系如图:
∴南门(0,0),狮子(﹣4,5),飞禽(3,4)两栖动物(4,1).
4.(2018春?荣昌县期末)如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
【思路点拨】分别过C点和B点作x轴和y轴的平行线,如图,然后利用S四边形ABCO=S矩形OHEF﹣S△ABH﹣S△CBE﹣S△OCF进行计算.
【答案与解析】
解:分别过C点和B点作x轴和y轴的平行线,如图,
则E(5,3),
所以S四边形ABCO=S矩形OHEF﹣S△ABH﹣S△CBE﹣S△OCF
=5×3﹣×2×2﹣×1×3﹣×3×2
=.
【总结升华】本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;会运用面积的和差计算不规则图形的面积.
举一反三:
【变式】在平面直角坐标系中,O为坐标原点,已知:A(3,2),B(5,0),则△AOB的面积为 .
【答案】5.
类型三、坐标平面及点的特征
5. (2019春?宜阳县期中)已知点P(2m+4,m﹣1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣3)点,且与x轴平行的直线上.
【思路点拨】(1)根据横纵坐标的大小关系得出m﹣1﹣(2m+4)=3,即可得出m的值,进而得出P点坐标;
(2)根据平行于x轴点的坐标性质得出m﹣1=﹣3,进而得出m的值,进而得出P点坐标.
【答案与解析】
解:(1)∵点P(2m+4,m﹣1),点P的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,
解得:m=﹣8,
∴2m+4=﹣12,m﹣1=﹣9,
∴点P的坐标为:(﹣12,﹣9);
(2)∵点P在过A(2,﹣3)点,且与x轴平行的直线上,
∴m﹣1=﹣3,
解得:m=﹣2,
∴2m+4=0,
∴P点坐标为:(0,﹣3).
【总结升华】此题主要考查了坐标与图形的性质,根据已知得出关于m的等式是解题关键.
举一反三:
【变式】在直角坐标系中,点P(x,y)在第二象限且P到x轴,y轴的距离分别为2,5,则P的坐标是_________;若去掉点P在第二象限这个条件,那么P的坐标是________.
【答案】(-5,2);(5,2),(-5,2),(5,-2),(-5,-2).
【巩固练习】
一、选择题
1.为确定一个平面上点的位置,可用的数据个数为( ).
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是( ).
A.(2,3)和(3,2)表示的位置相同
B.(2,3)和(3,2)是表示不同位置的两个有序数对
C.(2,2)和(2,2)表示两个不同的位置
D.(m,n)和(n,m)表示的位置不同
3.(2019?大连)在平面直角坐标系中,点M(1,5)所在的象限是( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.若点P(m,n)在第三象限,则点Q(-m,-n)在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.知点P(m+3,2m+4)在y轴上,那么点P的坐标是( ).
A.(-2,0) B.(0,-2) C.(1,0) D.(0,1)
6.(2018?北京)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A.景仁宫(4,2)? B.养心殿(﹣2,3)
C.保和殿(1,0) D.武英殿(﹣3.5,﹣4)
二、填空题
7.已知有序数对(2x-1,5-3y)表示出的点为(5,2),则x=________,y=________.
8.某宾馆一大楼客房是按一定规律编号的,例如房间403号是指该大楼中第4层第3个房间, 则房间815号是指第________层第________个房间;第6层第1个房间编号为________.
9. 点P(-3,4)到x轴的距离是________,到y轴的距离是________.
10.指出下列各点所在象限或坐标轴:
点A(5,-3)在_______,点B(-2,-1)在_______,点C(0,-3)在_______,点D(4,0)在_______,点E(0,0)在_______.
11.(2019?黔南州)在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
12.(2018?安溪县模拟)若点(3﹣x,x﹣1)在第二象限,则x的取值范围是 .
三、解答题
13.在图中建立适当的平面直角坐标系,使A、B两点的坐标分别为(-4,1)和(-1,4),写出点C、D的坐标,并指出它们所在的象限.
14.(2018春?夏津县校级期中)根据要求解答下列问题:
设M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意实数,且b<0时,点M位于何处?
15. 已知A,B,C,D的坐标依次为(4,0),(0,3),(-4,0),(0,-3),在平面直角坐标系中描出各点,并求四边形ABCD的面积.
【答案与解析】
一、选择题
1. 【答案】B.
2. 【答案】B.
3. 【答案】B;
【解析】四个象限的点的坐标符号分别是(+,+),(-,+),(-,-),(+,-).
4. 【答案】A;
【解析】因为点P(m,n)在第三象限,所以m,n均为负,则它们的相反数均为正.
5. 【答案】B;
【解析】m+3=0,∴m=-3,将其代入得:2m+4=-2,∴P(0,-2).
6. 【答案】B;
【解析】解:根据表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),
可得:原点是中和殿,
所以可得景仁宫(2,4),养心殿(﹣2,3),保和殿(0,1),武英殿(﹣3.5,﹣3),故选B.
二、填空题
7. 【答案】3,1;
【解析】由2x-1=5,得x=3;由5-3y=2,得y=1.
8. 【答案】8, 15, 601;
9. 【答案】4, 3;
【解析】到x轴的距离为:│4│=4,到y轴的距离为:│-3│=3.
10.【答案】第四象限,第三象限,y轴的负半轴上,x轴的正半轴上,坐标原点.
11.【答案】(﹣3,4)
【解析】解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).
12.【答案】x>3;
【解析】解:∵点(3﹣x,x﹣1)在第二象限,
∴,
解不等式①得,x>3,
解不等式②得,x>1,
所以不等式组的解集是x>3.
故答案为:x>3.
三、解答题
13.【解析】
解:建立平面直角坐标系如图:
得C(-1,-2)、D(2,1).由图可知,点C在第三象限,点D在第一象限.
14.【解析】
解:∵M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第四象限;
(2)当ab>0时,即a,b同号,故点M位于第一、三象限;
(3)当a为任意实数,且b<0时,点M位于第三、四象限和纵轴的负半轴.
15.【解析】
解:描点如下:
.
【学习目标】
1.了解确定位置的方法,用有序数对或用方向和距离来确定物体的位置.
2.理解平面直角坐标系概念,能正确画出平面直角坐标系.
2.能在平面直角坐标系中,根据坐标描出点的位置、由点的位置写出它的坐标.
3.会用确定坐标、描点、连线的方法在直角坐标系中作出简单图形.
【要点梳理】
要点一、确定位置的方法
有序数对:把有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b).
要点诠释:
有序,即两个数的位置不能随意交换,(a,b)与(b,a)顺序不同,含义就不同,如电影院的座位是6排7号,可以写成(6,7)的形式,而(7,6)则表示7排6号.
可以用有序数对确定物体的位置,也可以用方向和距离来确定物体的位置(或称方位).
要点二、平面直角坐标系与点的坐标的概念
1.平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系.水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点(如图1).
要点诠释:平面直角坐标系是由两条互相垂直且有公共原点的数轴组成的.
2.点的坐标
平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标,记作:P(a,b),如图2.
要点诠释:
(1)表示点的坐标时,约定横坐标写在前,纵坐标写在后,中间用“,”隔开.
(2)点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离.
(3) 对于坐标平面内任意一点都有唯一的一对有序数对(x,y)和它对应,反过来对于任意一对有序数对,在坐标平面内都有唯一的一点与它对应,也就是说,坐标平面内的点与有序数对是一一对应的.
要点三、坐标平面
1. 象限
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限和第四象限,如下图.
要点诠释:
(1)坐标轴x轴与y轴上的点(包括原点)不属于任何象限.
(2)按方位来说:第一象限在坐标平面的右上方,第二象限在左上方,第三象限在左下方,第四象限在右下方.
2.各个象限内和坐标轴上点的坐标的符号特征
要点诠释:
(1)对于坐标平面内任意一个点,不在这四个象限内,就在坐标轴上.
(2)坐标轴上点的坐标特征:x轴上的点的纵坐标为0;y轴上的点的横坐标为0.
(3)根据点的坐标的符号情况可以判断点在坐标平面上的大概位置;反之,根据点在坐标平面上的位置也可以判断点的坐标的符号情况.
【典型例题】
类型一、确定物体的位置
1.如果将一张“13排10号”的电影票简记为(13,10),那么(10,13)表示的电影票是 排 号.
【思路点拨】在平面上,一个数据不能确定平面上点的位置.须用有序数对来表示平面内点的位置.
【答案】10,13.
【解析】由条件可知:前面的数表示排数,后面的数表示号数.
【总结升华】在表示时,先要“约定”顺序,一旦顺序“约定”,两个数的位置就不能随意交换,(a,b)与(b,a)顺序不同,含义就不同.
2.如图,雷达探测器测得六个目标A、B、C、D、E、F出现.按照规定的目标表示方法,目标C、F的位置表示为C(6,120°)、F(5,210°).按照此方法在表示目标A、B、D、E的位置时,其中表示不正确的是( )
A.A(5,30°) B.B(2,90°) C.D(4,240°) D.E(3,60°)
【思路点拨】按已知可得,表示一个点,横坐标是自内向外的环数,纵坐标是所在列的度数,分别判断各选项即可得解.
【答案】D.
【解析】
由题意可知A、B、D、E的坐标可表示为:A(5,30°),故A正确;B(2,90°),故B正确;D(4,240°),故C正确;E(3,300°),故D错误.
【总结升华】本题考查了学生的阅读理解能力,由已知条件正确确定点的位置是解决本题的关键.
类型二、平面直角坐标系与点的坐标的概念
3.如图,写出点A、B、C、D各点的坐标.
【思路点拨】要确定点的坐标,要先确定点所在的象限,再看点到坐标轴的距离.
【答案与解析】
解:由点A向x轴作垂线,得A点的横坐标是2,再由点A向y轴作垂线,得A点的纵坐标是3,则点A的坐标是(2,3),同理可得点B、C、D的坐标.
所以,各点的坐标:A(2,3),B(3,2),C(-2,1),D(-1,-2).
【总结升华】平面直角坐标系内任意一点到x轴的距离是这点纵坐标的绝对值,到y轴的距离是这点横坐标的绝对值.
举一反三:
【变式】(2018春?临沂期末)多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道马场的坐标为(﹣3,﹣3),你能帮她建立平面直角坐标系并求出其他各景点的坐标?
【答案】解:建立坐标系如图:
∴南门(0,0),狮子(﹣4,5),飞禽(3,4)两栖动物(4,1).
4.(2018春?荣昌县期末)如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
【思路点拨】分别过C点和B点作x轴和y轴的平行线,如图,然后利用S四边形ABCO=S矩形OHEF﹣S△ABH﹣S△CBE﹣S△OCF进行计算.
【答案与解析】
解:分别过C点和B点作x轴和y轴的平行线,如图,
则E(5,3),
所以S四边形ABCO=S矩形OHEF﹣S△ABH﹣S△CBE﹣S△OCF
=5×3﹣×2×2﹣×1×3﹣×3×2
=.
【总结升华】本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;会运用面积的和差计算不规则图形的面积.
举一反三:
【变式】在平面直角坐标系中,O为坐标原点,已知:A(3,2),B(5,0),则△AOB的面积为 .
【答案】5.
类型三、坐标平面及点的特征
5. (2019春?宜阳县期中)已知点P(2m+4,m﹣1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣3)点,且与x轴平行的直线上.
【思路点拨】(1)根据横纵坐标的大小关系得出m﹣1﹣(2m+4)=3,即可得出m的值,进而得出P点坐标;
(2)根据平行于x轴点的坐标性质得出m﹣1=﹣3,进而得出m的值,进而得出P点坐标.
【答案与解析】
解:(1)∵点P(2m+4,m﹣1),点P的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,
解得:m=﹣8,
∴2m+4=﹣12,m﹣1=﹣9,
∴点P的坐标为:(﹣12,﹣9);
(2)∵点P在过A(2,﹣3)点,且与x轴平行的直线上,
∴m﹣1=﹣3,
解得:m=﹣2,
∴2m+4=0,
∴P点坐标为:(0,﹣3).
【总结升华】此题主要考查了坐标与图形的性质,根据已知得出关于m的等式是解题关键.
举一反三:
【变式】在直角坐标系中,点P(x,y)在第二象限且P到x轴,y轴的距离分别为2,5,则P的坐标是_________;若去掉点P在第二象限这个条件,那么P的坐标是________.
【答案】(-5,2);(5,2),(-5,2),(5,-2),(-5,-2).
【巩固练习】
一、选择题
1.为确定一个平面上点的位置,可用的数据个数为( ).
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是( ).
A.(2,3)和(3,2)表示的位置相同
B.(2,3)和(3,2)是表示不同位置的两个有序数对
C.(2,2)和(2,2)表示两个不同的位置
D.(m,n)和(n,m)表示的位置不同
3.(2019?大连)在平面直角坐标系中,点M(1,5)所在的象限是( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.若点P(m,n)在第三象限,则点Q(-m,-n)在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.知点P(m+3,2m+4)在y轴上,那么点P的坐标是( ).
A.(-2,0) B.(0,-2) C.(1,0) D.(0,1)
6.(2018?北京)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A.景仁宫(4,2)? B.养心殿(﹣2,3)
C.保和殿(1,0) D.武英殿(﹣3.5,﹣4)
二、填空题
7.已知有序数对(2x-1,5-3y)表示出的点为(5,2),则x=________,y=________.
8.某宾馆一大楼客房是按一定规律编号的,例如房间403号是指该大楼中第4层第3个房间, 则房间815号是指第________层第________个房间;第6层第1个房间编号为________.
9. 点P(-3,4)到x轴的距离是________,到y轴的距离是________.
10.指出下列各点所在象限或坐标轴:
点A(5,-3)在_______,点B(-2,-1)在_______,点C(0,-3)在_______,点D(4,0)在_______,点E(0,0)在_______.
11.(2019?黔南州)在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
12.(2018?安溪县模拟)若点(3﹣x,x﹣1)在第二象限,则x的取值范围是 .
三、解答题
13.在图中建立适当的平面直角坐标系,使A、B两点的坐标分别为(-4,1)和(-1,4),写出点C、D的坐标,并指出它们所在的象限.
14.(2018春?夏津县校级期中)根据要求解答下列问题:
设M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意实数,且b<0时,点M位于何处?
15. 已知A,B,C,D的坐标依次为(4,0),(0,3),(-4,0),(0,-3),在平面直角坐标系中描出各点,并求四边形ABCD的面积.
【答案与解析】
一、选择题
1. 【答案】B.
2. 【答案】B.
3. 【答案】B;
【解析】四个象限的点的坐标符号分别是(+,+),(-,+),(-,-),(+,-).
4. 【答案】A;
【解析】因为点P(m,n)在第三象限,所以m,n均为负,则它们的相反数均为正.
5. 【答案】B;
【解析】m+3=0,∴m=-3,将其代入得:2m+4=-2,∴P(0,-2).
6. 【答案】B;
【解析】解:根据表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),
可得:原点是中和殿,
所以可得景仁宫(2,4),养心殿(﹣2,3),保和殿(0,1),武英殿(﹣3.5,﹣3),故选B.
二、填空题
7. 【答案】3,1;
【解析】由2x-1=5,得x=3;由5-3y=2,得y=1.
8. 【答案】8, 15, 601;
9. 【答案】4, 3;
【解析】到x轴的距离为:│4│=4,到y轴的距离为:│-3│=3.
10.【答案】第四象限,第三象限,y轴的负半轴上,x轴的正半轴上,坐标原点.
11.【答案】(﹣3,4)
【解析】解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).
12.【答案】x>3;
【解析】解:∵点(3﹣x,x﹣1)在第二象限,
∴,
解不等式①得,x>3,
解不等式②得,x>1,
所以不等式组的解集是x>3.
故答案为:x>3.
三、解答题
13.【解析】
解:建立平面直角坐标系如图:
得C(-1,-2)、D(2,1).由图可知,点C在第三象限,点D在第一象限.
14.【解析】
解:∵M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第四象限;
(2)当ab>0时,即a,b同号,故点M位于第一、三象限;
(3)当a为任意实数,且b<0时,点M位于第三、四象限和纵轴的负半轴.
15.【解析】
解:描点如下:
.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
